特征工程
特征工程
首先, 明确一点, 机器学习的效果好坏更多的取决于 对数据的处理是否到位.. 也就是说 数据处理的重要性是大于训练的.
处理数据可以让数据更加纯净, 也就更容易找到规律, 训练的结果也就更好..
我们知道样本数据可分为两类, 一类是特征、一类是标签. 我们往往对样本中的特征数据进行处理, 样本中的标签数据一般不用.
特征工程中所谓的特征, 指的就是样本数据组成中的特征数据, 特征工程也就是对样本中的特征数据进行相关的操作.
有这么一句话广为流传: 特征决定了机器学习的上限, 而模型和算法只是逼近这个上限而已.
不对数据进行特征工程的处理,用再好的算法,可能也就将正确率从30%提升到35%.
而我先对数据进行特征工程处理,再使用算法,哪怕这个算法不是最优秀的,正确率也可以达到百分之90%.
2
特征工程可以通过 sklearn工具来进行实现. 大体有三个操作(这三个操作有顺序之分的,依次递进):
-1- 特征抽取
-2- 特征无量纲化
-3- 特征选择
# 特征抽取
将样本中 [非数值形式] 的特征 [转换] 成模型可以接收的 [数值] 形式, 这个过程也可以成为 "特征值化".
Why?
我们知道, 训练模型的时候需要将样本数据带入到模型内部的算法中进行相关的数学运算.
只有数值形式的数据才可以进行数学运算, 所以模型只可以接收数值形式的特征数据. 因此,我们要进行 "特征值化".
思考: 样本中的标签数据是不是也必须为数值型数据呢?
不一定, 取决于在模型训练的过程中, 标签数据是否参与了模型的训练. (算法模型分类, 有监督还是无监督的)
若参与了, 则要求标签数据必须为数值型数据; 若没有参与运算, 则无需为数值型数据.
敲黑板: 非数值型数据的分类
-1- 有序分类变量 - 有级别顺序之分, eg: 高中-本科-研究生; M-L-XL-XXL
-2- 无序分类变量 - 每个类别是等同的, eg: 颜色; 血型; 民族; 性别.
☆ 注意: 特征抽取的过程中, 需要尽可能的保证特征值化之前和之后的数据含义和信息总量保持不变或者出入不大!
特征抽取有三个实现方案:
-1- 独热编码 (One-Hot Encoding). - 无序
-2- 标签编码 (Label Encoding). - 有序
-3- 文本向量化 (Text Vectorization)
# 独热编码
概念: 独热编码可以将原始的特征转换为二进制向量, 其中每个特征只有一个取值为1, 其他取值为0. (听不懂? 看示例就明白了)
应用场景: 适用于 无序分类变量 的特征. eg 颜色、尺码等
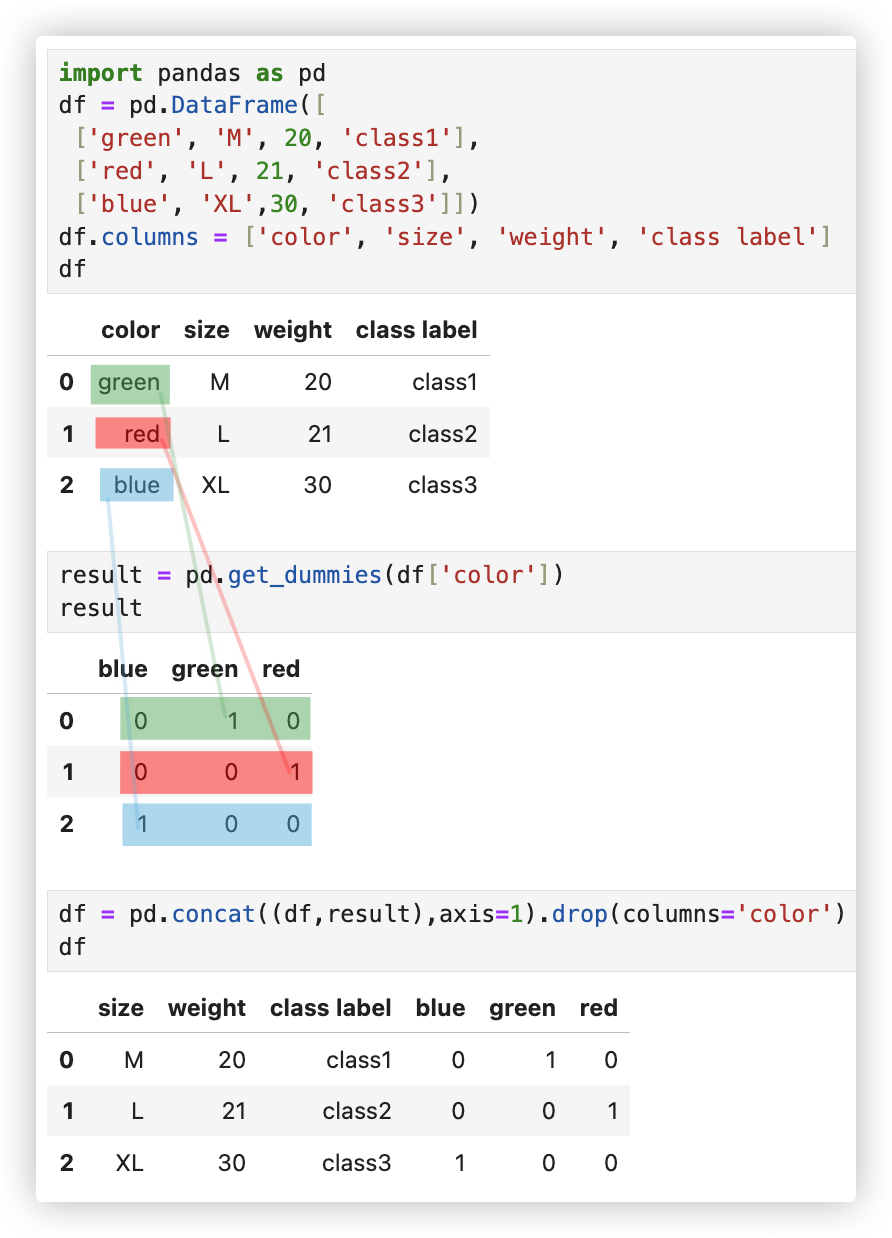
示例: 对color这一无序分类变量特征进行one-hot编码.
import pandas as pd
df = pd.DataFrame([
['green', 'M', 20, 'class1'],
['red', 'L', 21, 'class2'],
['blue', 'XL',30, 'class3']])
df.columns = ['color', 'size', 'weight', 'class label']
df
result = pd.get_dummies(df['color'])
result
df = pd.concat((df,result),axis=1).drop(columns='color')
df
2
3
4
5
6
7
8
9
10
11
12
13
思考: 用1、2、3分别代表 green、red、blue? no, 这样搞就有大小级别之分了.. 颜色是无序类别变量.
# 标签编码
概念: 标签编码可以将原始的特征转换为从0到N-1的整数, 其中N表示不同取值的数量.
应用场景: 适用于 有序分类变量 的特征. eg 学历、评级 等
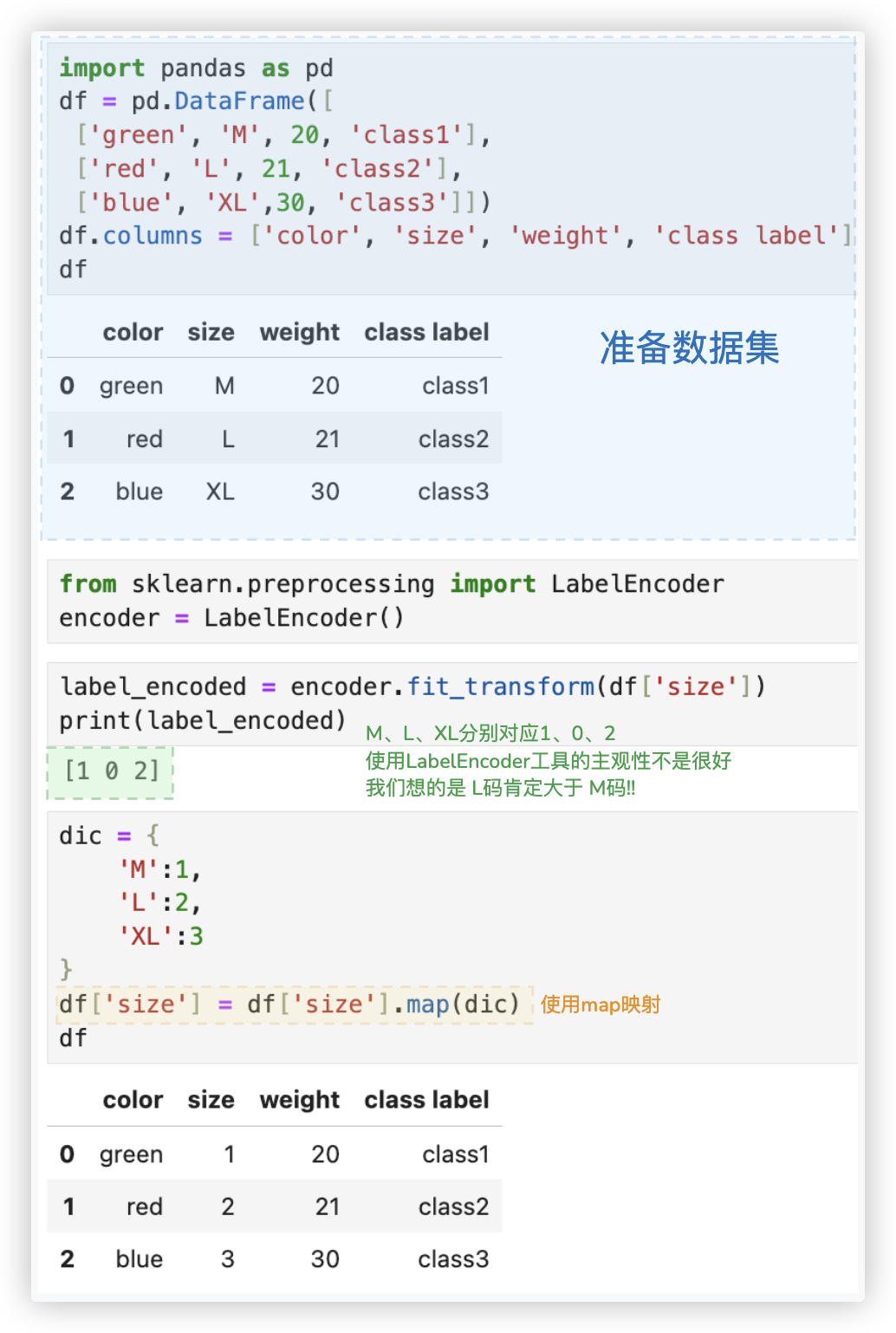
实现方式有两种, 一是用map映射, 二是使用LabelEncoder工具.
前者主观性更好,我们一般会使用该方案来实现; 后者的排序规则是根据首字母大小,主观性差.
示例: 将size这一有序分类特征进行标签编码.
import pandas as pd
df = pd.DataFrame([
['green', 'M', 20, 'class1'],
['red', 'L', 21, 'class2'],
['blue', 'XL',30, 'class3']])
df.columns = ['color', 'size', 'weight', 'class label']
df
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
label_encoded = encoder.fit_transform(df['size'])
print(label_encoded)
dic = {
'M':1,
'L':2,
'XL':3
}
df['size'] = df['size'].map(dic)
df
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 文本向量化 - 词频统计
若特征不是一个单词, 而是一段话一个文本呢? 就需要使用文本向量化来进行特征提取..
实现文本向量化的特征提取有两种方案.
简单来说, 第一种是基于 频率; 第二种是 基于 权重/重要程度. 这两种方案没有优劣之分, 哪个方案的效果好就用哪个!
先来康康基于出现频率的词频统计.
# 英文简单版
进行词频统计, 将统计的词频作为文本向量化的结果.
该示例在两篇文本中提取了8个单词,并计算出了每个单词在第一篇第二篇文本中出现的次数..
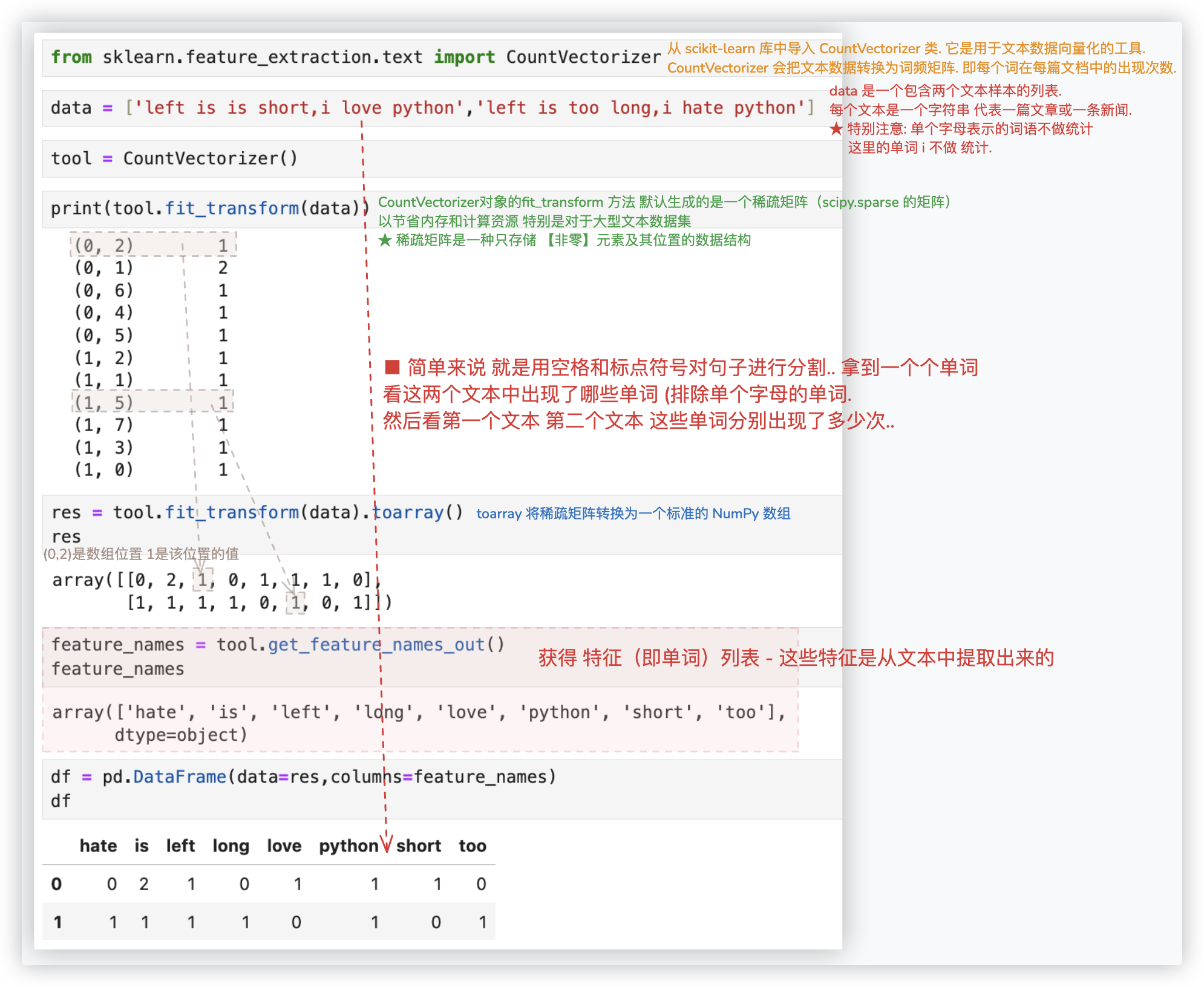
from sklearn.feature_extraction.text import CountVectorizer
data = [
'left is is short,i love python',
'left is too long,i hate python'
]
tool = CountVectorizer()
print(tool.fit_transform(data))
res = tool.fit_transform(data).toarray()
res
feature_names = tool.get_feature_names_out()
feature_names
df = pd.DataFrame(data=res,columns=feature_names)
df
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
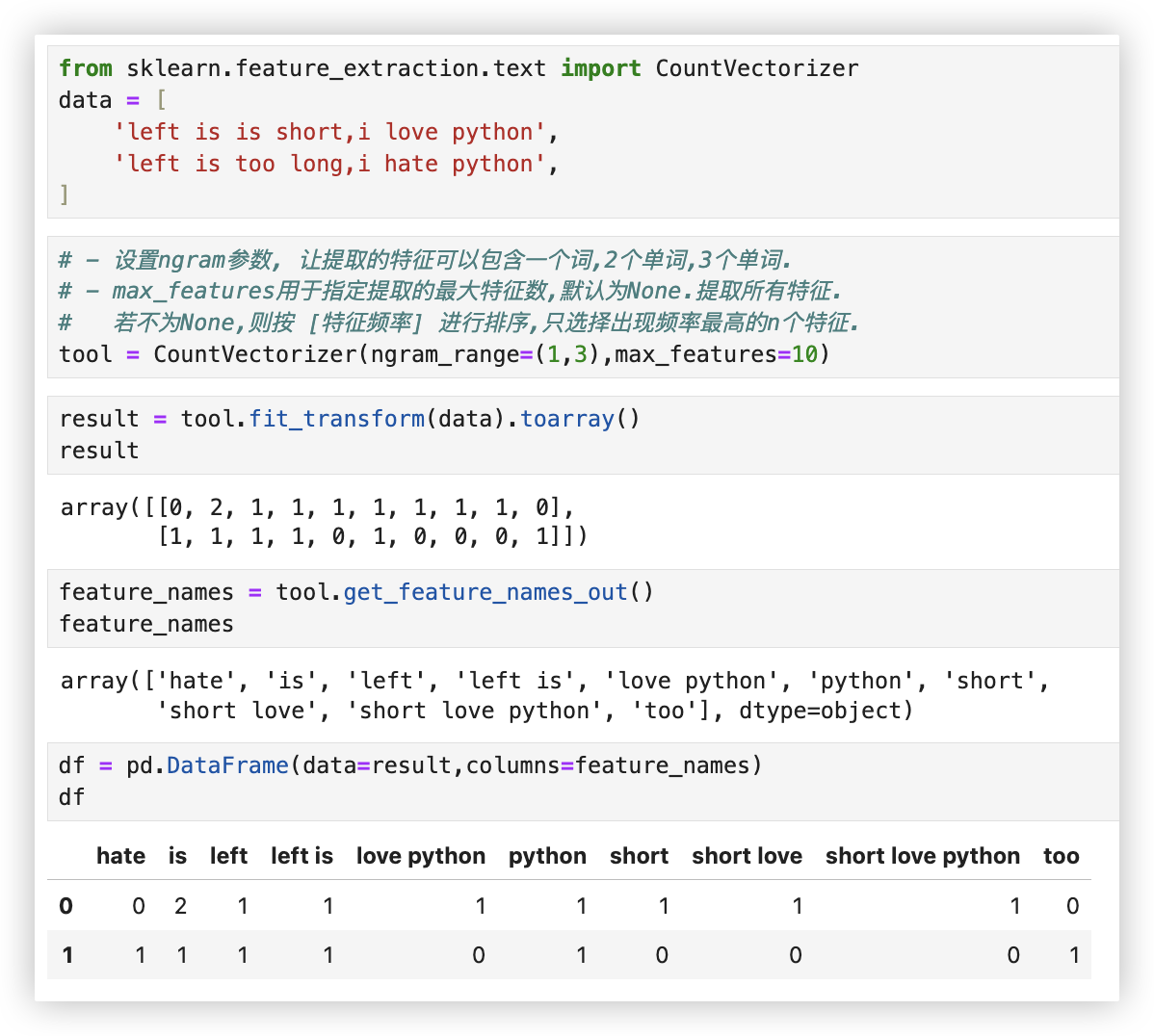
# 英文优化版
上面的词频统计-英文简单版, 感觉有点过于简单了.
只考虑了单个单词的词频, 并没有考虑词出现的位置以及先后顺序.. 那如何改进呢?
我们可以通过设置ngram_range参数来控制特征的复杂度.
比如我们不光可以考虑单单一个词, 还可以考虑两个词连在一起, 甚至更多的词连在一起..
★ 优化后, 特征就考虑了上下文的前后关系. 通常情况下, ngram_range 参数设置基本为2就够了
from sklearn.feature_extraction.text import CountVectorizer
data = [
'left is is short,i love python',
'left is too long,i hate python',
]
"""
跟之前的单个词来对比,这回我们得到的特征更复杂了一些,特征的长度也明显变多了.
可以考虑到上下文的前后关系了,但是这只是我们举的一个简单小例子,看起来还没什么问题.
如果实际文本中出现词的个数成千上万了呢? 那使用ngram_range=(1,4)参数,得到的词向量的长度就太长了,用起来就很麻烦了.
所以通常情况下,ngram_range参数设置基本为2就够了,再多计算起来就成累赘了!
"""
tool = CountVectorizer(ngram_range=(1,3),max_features=10)
result = tool.fit_transform(data).toarray()
result
feature_names = tool.get_feature_names_out()
feature_names
df = pd.DataFrame(data=result,columns=feature_names)
df
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 文本向量化 - TF-IDF
TF先,IDF后. TF词频统计,IDF看特征的通用性.
Q: 仅仅进行了词频统计后, 每个词出现的次数就可以表示原始特征文本的含义吗?
A: 显然是可以的, 但是会有较大的信息损失, 因此需要使用TF-IDF加以处理, 尽量减少特征值化后的信息损失.
当我们对《中国的蜜蜂养殖》进行词频统计的时候,发现这篇文章中:
'中国','蜜蜂','养殖'这三个词出现的次数是一样的,比如都是10次,那这个时候如果判断其重要性呢?
这一篇文章应该讲述的是都跟蜜蜂和养殖相关的技术,所以蜜蜂和养殖这俩词应当是重点了.
而中国这个词,我们既可以说中国的蜜蜂,还可以说中国的篮球,中国的大熊猫,能派上用场的地方简直太多了,没有那么专一.
所以在这篇文章中它应当不是那么重要的.
★ 这里我们就可以给出一个合理的定义了:
- 若一个词在整个语料库中(可以当作是在所有文章中)出现的次数都很高(这篇也有它,另一篇还有这个词).
那么这个词的重要程度就不高,因为它更像一个通用词.
- 若另一个词在整体的预料库中的词频很低,但是在这一篇文章中的词频却很高,我们就有理由认为它在这篇文章中就很重要了.
2
3
4
5
6
7
8
9
10
11
# 原理
简单阐述下,TF-IDF的原理, 不要纠结公式咋来的, 拿来用就行!
□ TF(Term Frequency): 衡量单个词语在文档中的出现频率. 它表示该词在文档中出现的次数与文档中总词数之比.
TF的计算公式为:
- TF = (某个词语在当前文本中出现的次数)/(要进行文本向量化的文本划分出的总词语数)
- 一个词在总文档中出现的频率越高,则该词的TF值越大
□ IDF(Inverse Document Frequency):
衡量词语在整个文档集合<即语料库>中的重要性.
它表示该词语对于区分不同文档的能力的高低(该词在该文档中出现的频率高,在其他文档中出现的频率低,则IDF高).
IDF通过对包含该词语的文档进行统计,以及总文档数进行统计,来计算词语的重要性.
IDF的计算公式为:
- IDF = log( (语料库的总文档数) / (包含该词语的语料库的文档数 + 1) )
+1是为了防止除数为0 -- 求10的多少次方等于(语料库的总文档数) / (包含该词语的语料库的文档数 + 1)
- 一个词在总文档中出现的频率越高,则“包含该词的文档数”相对会越多,否则IDF就会越低.
- TF-IDF:
TF-IDF用于衡量一个词语对于某个文档的重要性.它的计算公式为: `TF-IDF` = TF * IDF。
"""
a^x = N (a>0且a不等于1) 求x,则 x=loga^N 读作以a为底N的对数 若a=10 则a可用省略,简写成 x=log^N
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
★ TF-IDF的作用是给予每个词语一个权重, 越重要的词语的TF-IDF值越高!
(*≧ω≦) 简单来说:
对多篇要进行文本向量化的文档划分出词组后.. 统计某个词组在当前文档中的出现的频率 -- 这就是词频统计的过程哒.
若该频率高, 则TF高, 若这个词组在语料库中的出现次数很低, 则IDF高, 因而 TF-IDF会很高.(TF-IDF = TF * IDF)
# 英文文本处理
同词频统计一样,左侧是单个单词作为特征, 右侧是可以使用词组作为特征..
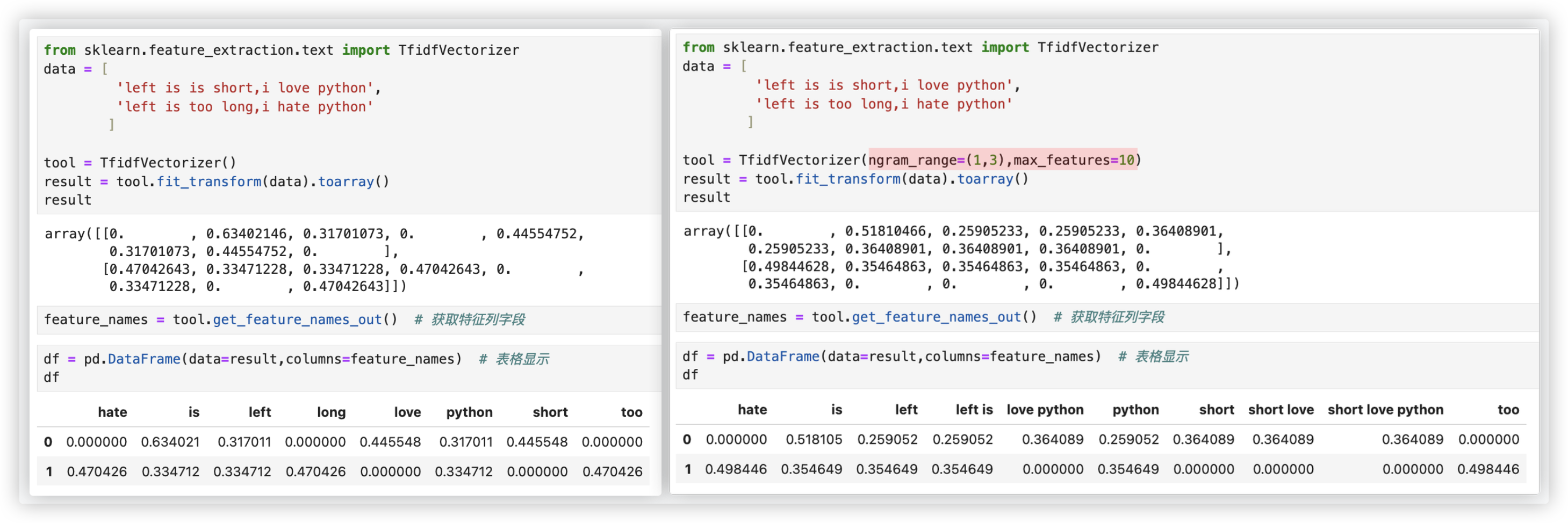
整体过程跟词频统计的代码差不多,CountVectorizer换成了TfidfVectorizer.. 而且它两划分出来的 词组/特征 都是一样.
from sklearn.feature_extraction.text import TfidfVectorizer
data = [
'left is is short,i love python',
'left is too long,i hate python'
]
tool = TfidfVectorizer(ngram_range=(1,3),max_features=10)
result = tool.fit_transform(data).toarray()
result
feature_names = tool.get_feature_names_out()
df = pd.DataFrame(data=result,columns=feature_names) # 表格显示
df
2
3
4
5
6
7
8
9
10
11
12
13
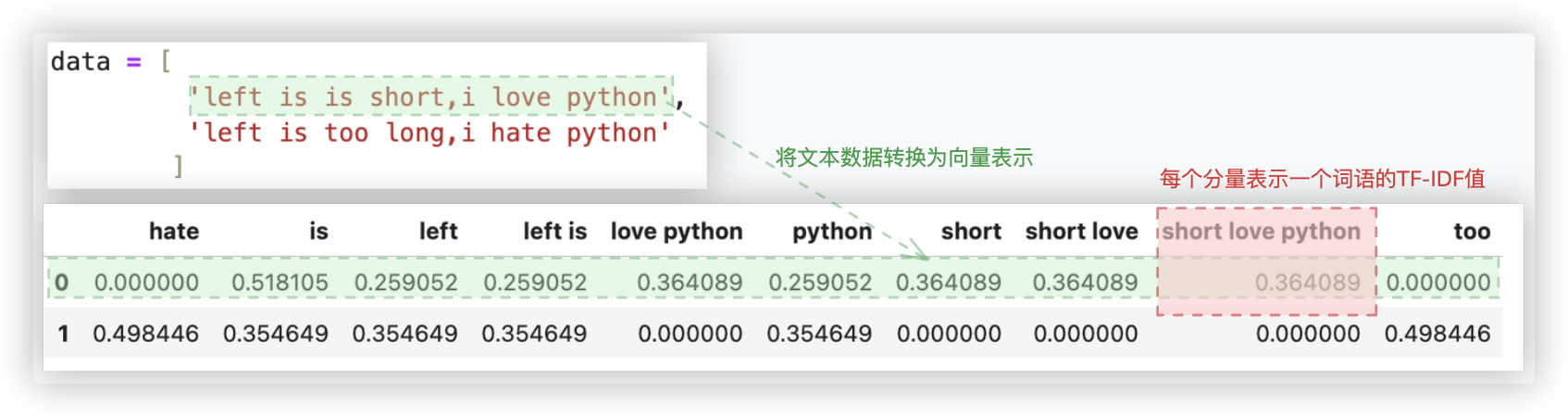
通过TF-IDF向量化,我们可以将文本数据转换为向量表示,其中每个分量表示一个词语的TF-IDF值.
这样可以忽略掉一些常见的无关词语, 突出重要的关键词, 进而用于文本特征表示、相似度计算、文本分类等任务.
# 中文文本处理
由于英文文本的每一个单词都是以空格分隔的, 因此TF-IDF可以根据空格提取每一个主词(单个字母表示的词语不做统计).
但是中文的词和词之间没有空格, 则无法直接进行主词的提取, 因此需要借助相关的中文分词工具进行主词的提取.
import jieba
word = '因为在自然语言处理中,我们是需要将一段中文文本中相关的词语,成语,形容词......都要进行抽取'
result = list(jieba.cut(word))
print(result)
"""
['因为', '在', '自然语言', '处理', '中', ',', '我们', '是', '需要', '将', '一段', '中文', '文本', '中', '相关', '的',
'词语', ',', '成语', ',', '形容词', '......', '都', '要', '进行', '抽取']
"""
2
3
4
5
6
7
8
9
分词后用空格进行拼接, 接着用英文文本的处理逻辑再进行处理 就没有问题.
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
data = [
'由于市场经济的影响,某些股票的走势出现了持续下滑的迹象',
'气象频道报道,收到持续强降水的影响,多地的农作物的收成出现了持续下滑的迹象'
]
# 保存分词后的结果
jieba_list = []
for line in data:
jieba_line = list(jieba.cut(line))
jieba_line = ' '.join(jieba_line)
jieba_list.append(jieba_line)
# TF-IDF向量化
# 注意: 单个字表示的词语不做统计
tool = TfidfVectorizer(max_features=10) # ngram_range,max_features参数,根据需求自己来.
result = tool.fit_transform(jieba_list).toarray()
# 获取特征列字段
feature_names = tool.get_feature_names_out()
# 表格显示
df = pd.DataFrame(data=result,columns=feature_names)
df
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 特征无量纲化
# 概念以及作用
在机器学习算法实践中, 我们往往有着将不同规格的数据转换到同一规格, 或不同分布的数据转换到某个特定分布的需求..
这种需求统称为将数据"无量纲化".
特征无量纲化技术的作用是消除不同特征之间的量纲差异, 使得它们具有可比性, 并且能够更好地适应不同的机器学习算法.
通过无量纲化, 可以提高特征的可解释性、降低模型学习的复杂性, 提高算法的稳定性和效果..
2
3
4
5
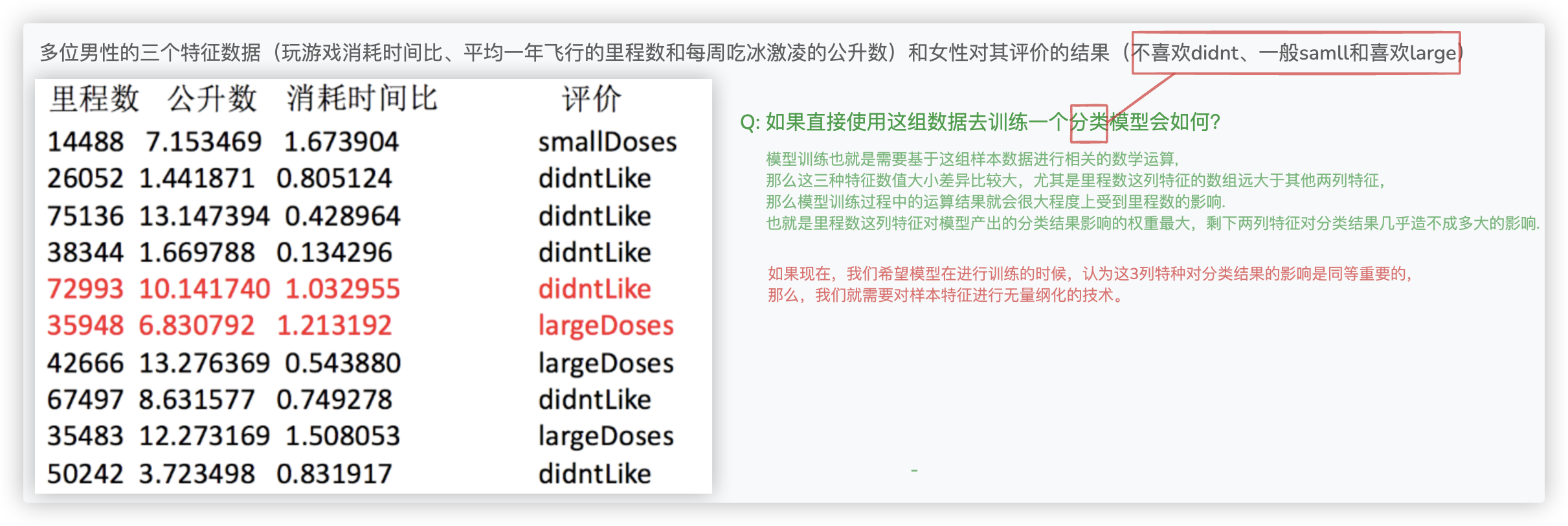
晕了吧?! 简单来说, 纲量差异通常指 每个特征/列 数据的数值差异.. 数值越大的,在机器学习生成模型的过程中越偏爱它!!
比如, 两列数据 [[10000,30],[10030,20],[13800,80],[12900,50]] 第一列数据的5位数第二列数据2位数.. 偏爱第一列数据!
我们希望机器学习在生成模型的过程中公平的考虑这 两个维度/两列的特征.. 就得使用特征无量纲化!
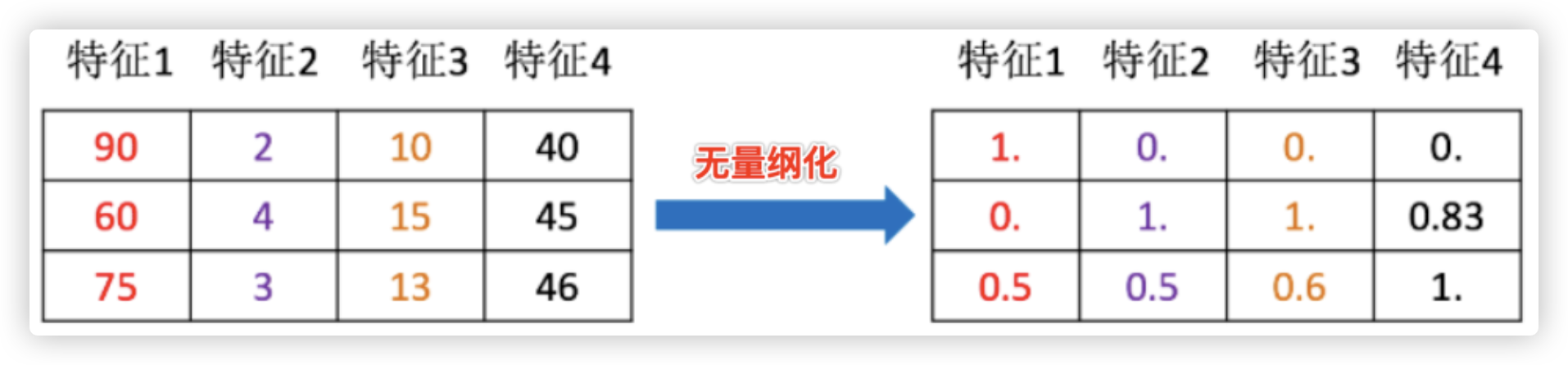
再用一个例子辅助说明:
特征的无量纲化我们通常使用 归一化和标准化 这两种技术来实现..
★ 如何选? 从各自的公式可以分析出, 归一化会受异常值的影响, 标准化对异常值不敏感, 所以我们通常选 标准化!!
建议先试试看StandardScaler, 效果不好换MinMaxScaler..
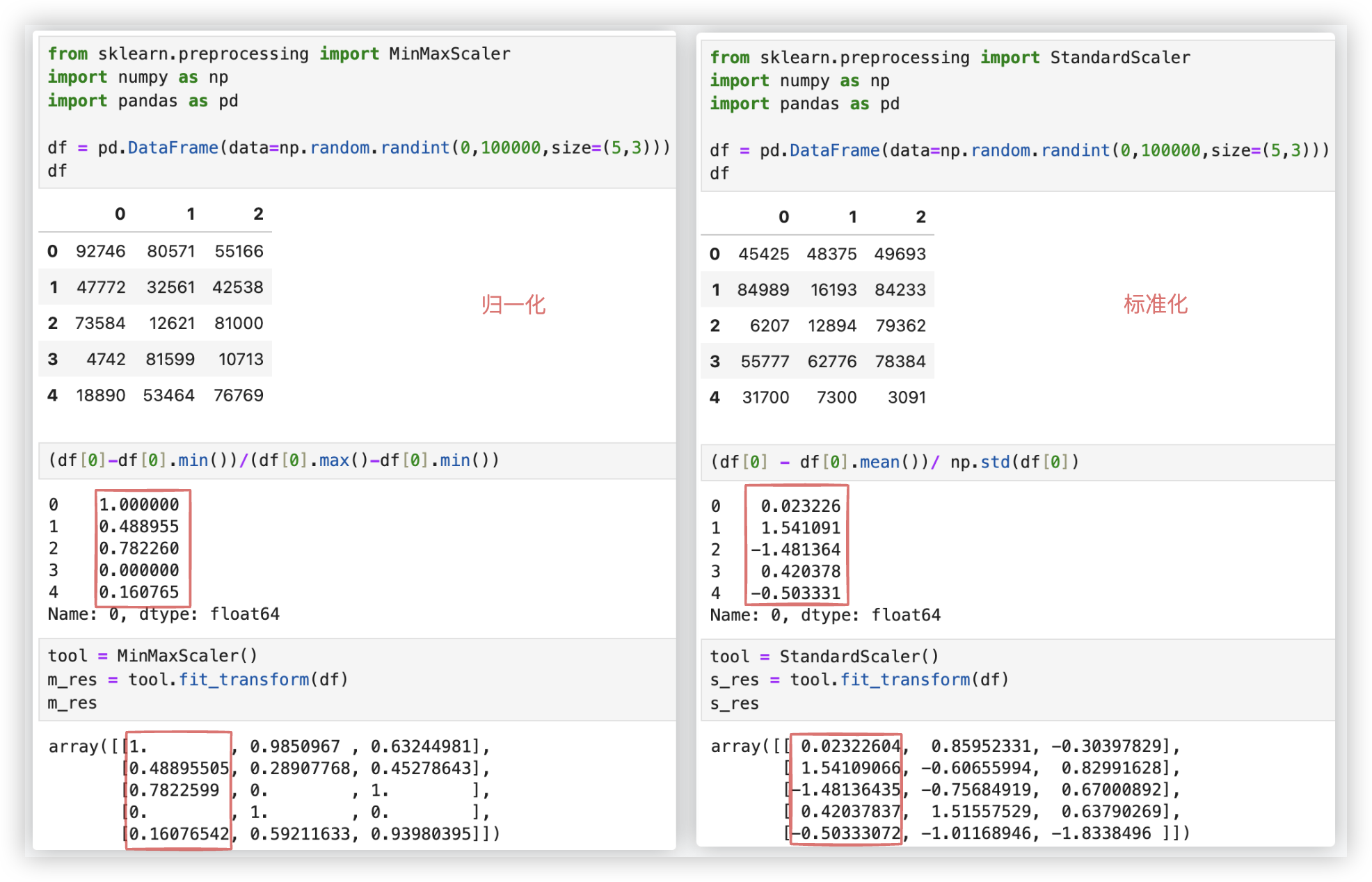
# 归一化
通过对原始数据进行变换把数据映射到(默认为[0,1])之间. 具体公式如下:
x代表这一列, max为一列的最大值, min为一列的最小值..
mx、mi 是闭区间的值, 默认mx 为1、mi 为0.. So, 默认情况下, x“=x'
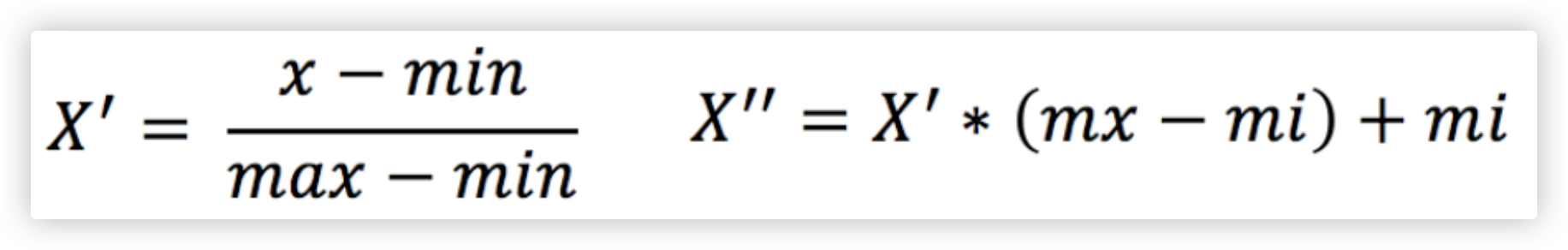
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import pandas as pd
df = pd.DataFrame(data=np.random.randint(0,100000,size=(5,3)))
df
(df[0]-df[0].min())/(df[0].max()-df[0].min())
tool = MinMaxScaler() # 参数feature_range表示缩放范围,通常使用默认值(0,1)
m_res = tool.fit_transform(df)
m_res
2
3
4
5
6
7
8
9
10
11
12
Q: 如果数据中存在的异常值(eg: 极大极小值)比较多, 会对结果造成什么样的影响?
A: 结合着归一化计算的公式可知, 极大极小值的影响很大!! So. 归一化无法很好的处理异常值!!
如何解决呢? 用标准化!
# 标准化
当数据按均值中心化后, 再按标准差缩放, 数据就会服从为均值为0, 方差为1的正态分布, 而这个过程就叫做数据标准化.
mean为平均值, σ 为标准差..
标准差: 每一项与均值相减的平方之和除以个数之后再开根号..
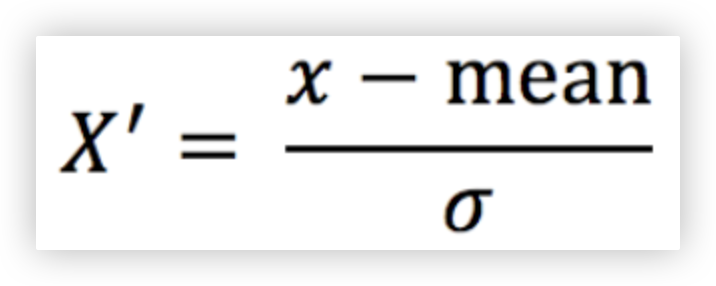
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
df = pd.DataFrame(data=np.random.randint(0,100000,size=(5,3)))
df
(df[0] - df[0].mean())/ np.std(df[0])
tool = StandardScaler()
s_res = tool.fit_transform(df)
s_res
2
3
4
5
6
7
8
9
10
11
12
# 特征选择
概述: 从特征中选择出有意义对模型有帮助的特征作为最终的机器学习输入的数据.
特征选择的原因:
-1- 冗余: 部分特征的相关度高, 容易消耗计算机的性能.
-2- 噪点: 部分特征对预测结果有偏执影响.
特征选择的技术实现:
-1- 人为对相关的特征进行主观选择.
-2- 方差过滤、PCA、相关系数、F检验 等等..
# 方差过滤
◎ 原理:
方差过滤是一种基于特征方差的特征选择方法. 其基本原理是通过计算特征的方差, 来评估特征的重要性.
方差是一种度量特征取值变化程度的统计量, 特征列数据的方差越大表示改特征列的数据波动较大(携带的信息量越大).
可能对于预测目标会具有更大的影响力。
◎ 方差过滤的步骤如下:
-1- 对数据集中的每个特征计算方差.
-2- 根据设定的阈值, 选择方差大于阈值的特征作为重要特征.
-3- 使用选定的重要特征进行模型训练和评估.
2
3
下面以一个具体的应用案例来说明方差过滤的原理:
假设我们有一个二分类问题的数据集, 包含100个样本和5个特征. 每个特征的方差如下表所示:
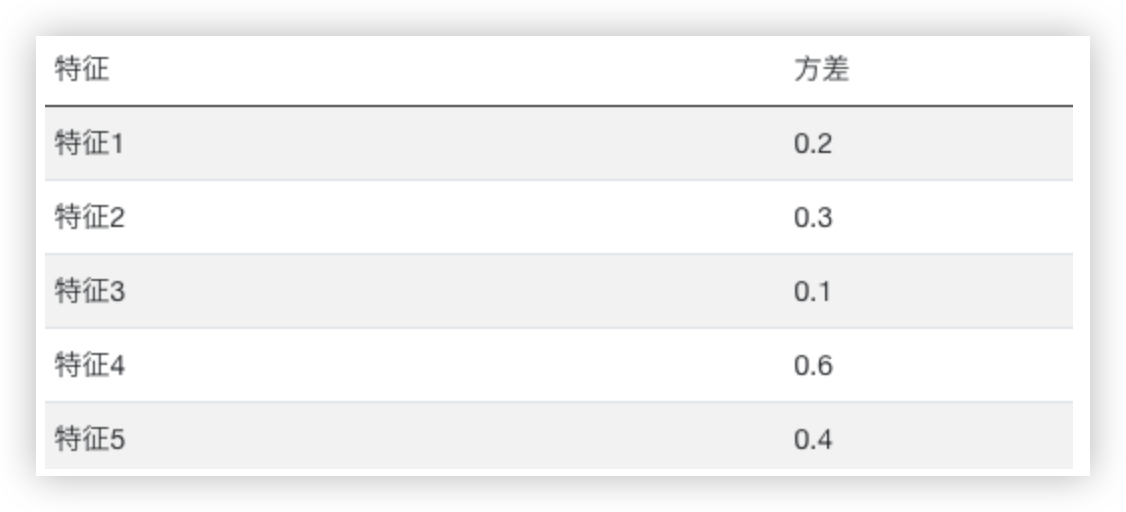
设定方差的阈值为0.3, 根据阈值筛选出方差大于0.3的特征.
根据表中的方差值, 我们可以看到特征1和特征3的方差小于阈值, 因此它们被认为是方差较低的特征, 可能对于预测目标的贡献较小.
而特征2、特征4和特征5的方差大于阈值,被认为是方差较高的特征, 可能对于预测目标具有更大的影响力.
因此,方差过滤会选择特征2、特征4和特征5作为重要特征!
在应用方差过滤的结果中,我们选择了特征2、特征4和特征5作为重要特征,可以在模型训练和评估过程中只使用这些特征.
这样可以减少特征数量,提高模型的训练效率,并有可能提高模型的预测性能.
综上所述:
方差过滤是一种基于特征方差来进行特征选择的方法,通过选择方差大于阈值的特征作为重要特征,可以帮助我们减少特征数量,并提高模型性能.
2
3
4
5
6
7
8
9
10
11
◎ 代码示例:
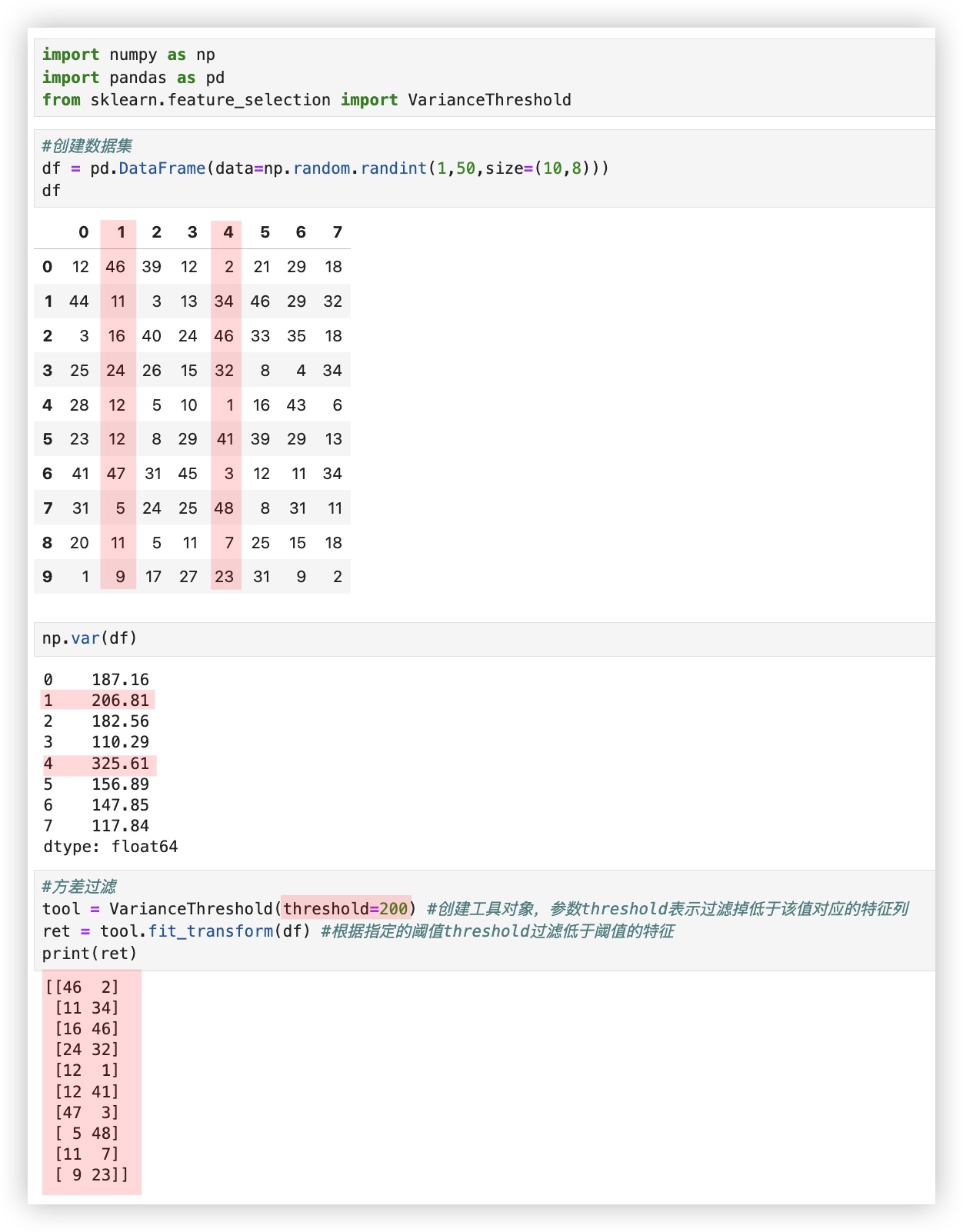
◎ Q: 方差过滤中的threshold阈值应该如何选取最优的值呢?
我们怎样知道, 方差过滤掉的到底时噪点特征还是有效特征呢? 过滤后模型到底会变好还是会变坏呢?
- 答案是,每个数据集不一样,只能自己去尝试.
- 关于threshold的取值,我们可以绘制模型的学习曲线来找寻最优的threshold取值.
- 学习曲线:
穷举不同的threshold值作用在方差过滤的特征选择中,然后以此尝试.
模型在哪个threshold值中表现是最好的就把该threshold值作为最优值.
- 但现实中,我们往往不会这样去做,因为这样会耗费大量的时间.
我们只会使用阈值为0或者阈值很小的方差过滤,来为我们优先消除一些明显用不到的特征.
然后我们会选择更优的特征选择方法继续削减特征数量。
2
3
4
5
6
7
8
# PCA
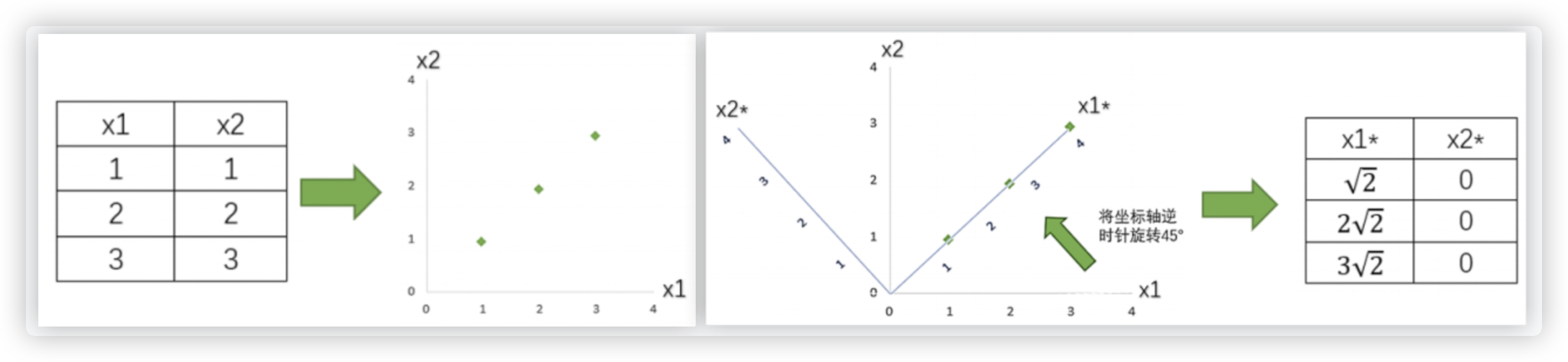
以二维特征降为一维特征为例, 是在一个直角坐标系中; 若是对三维特征降维,则是在一个空间坐标系中, 更高维度的就想象不到啦!
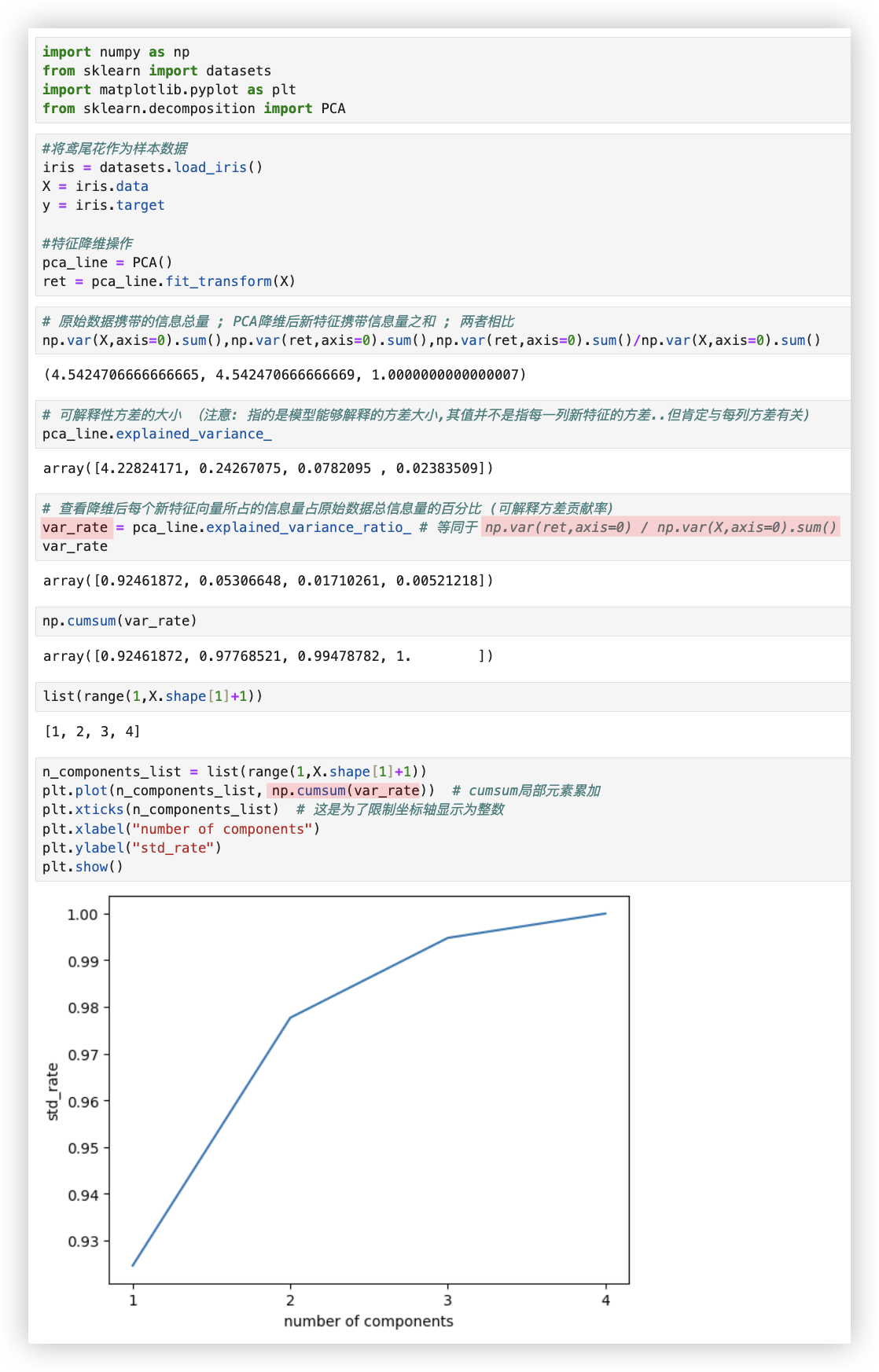
# 相关系数
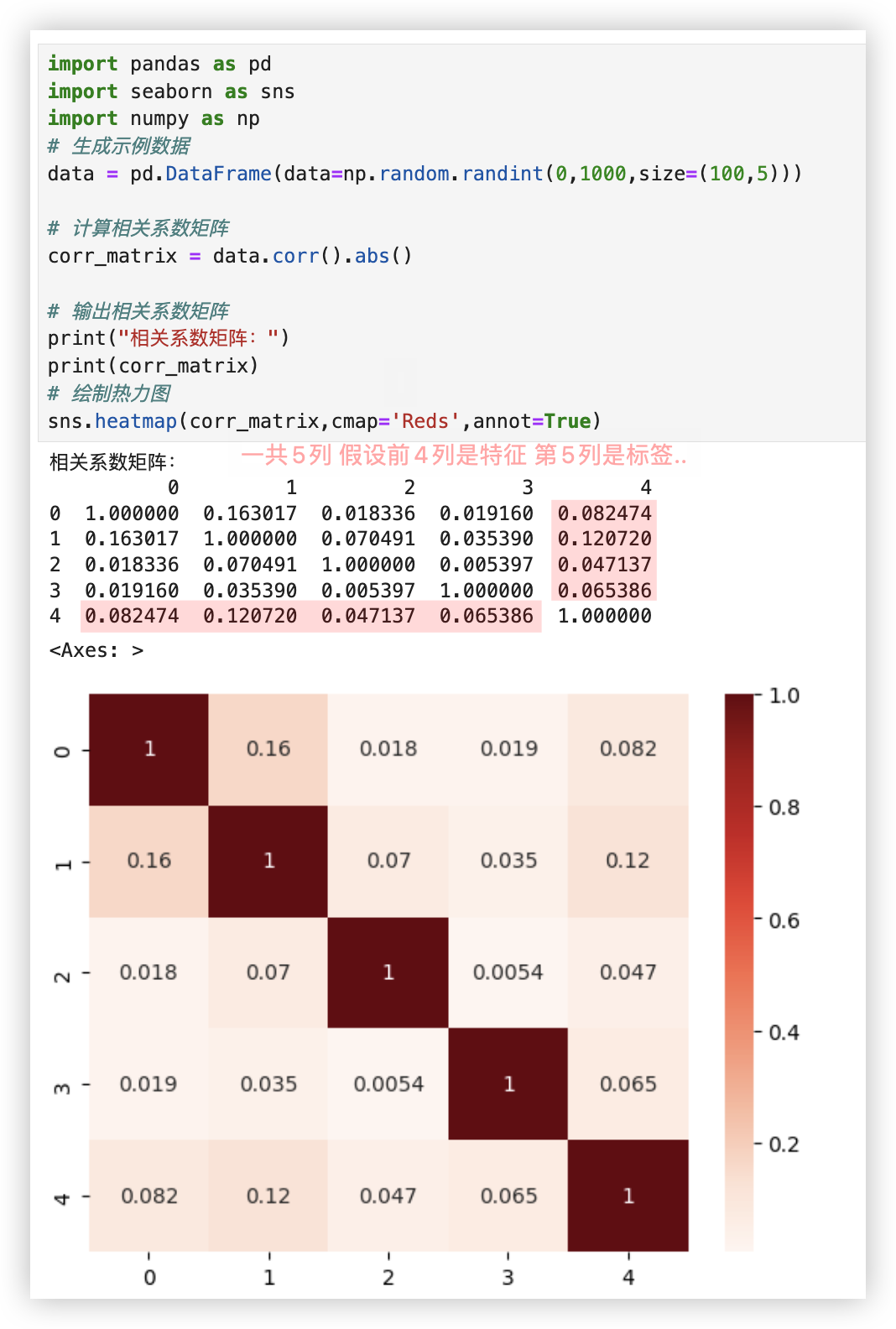
# F检验
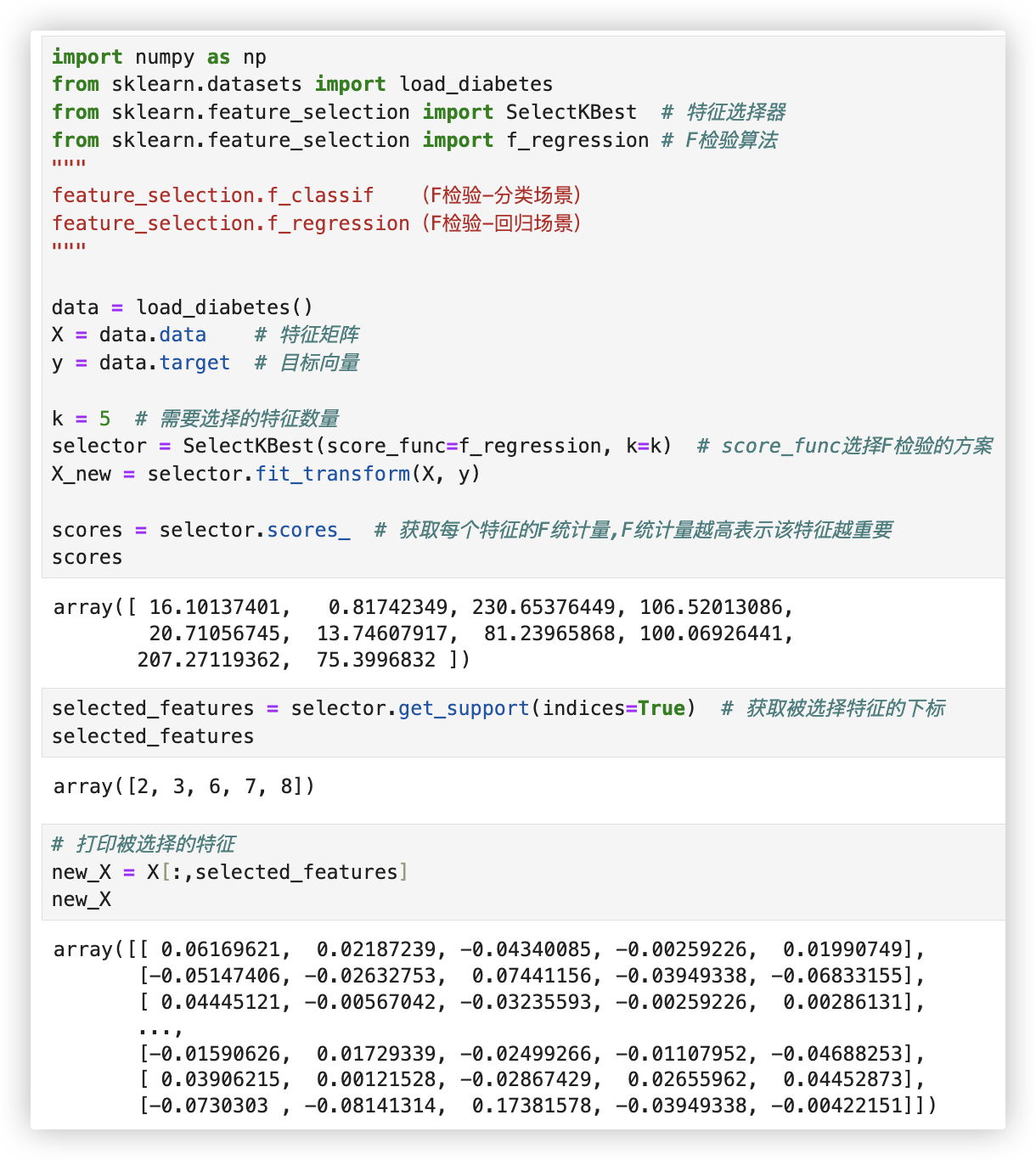
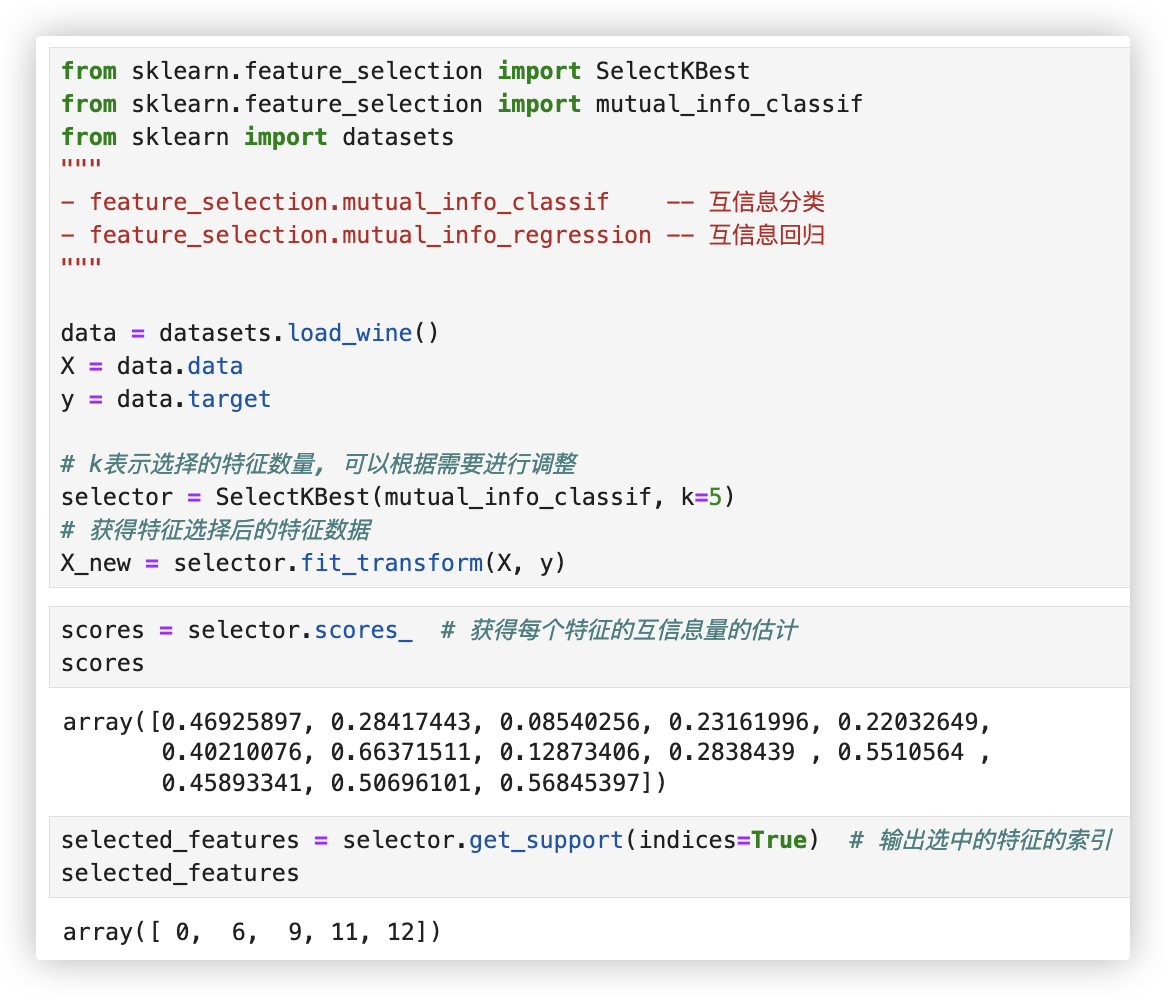
# 卡片过滤
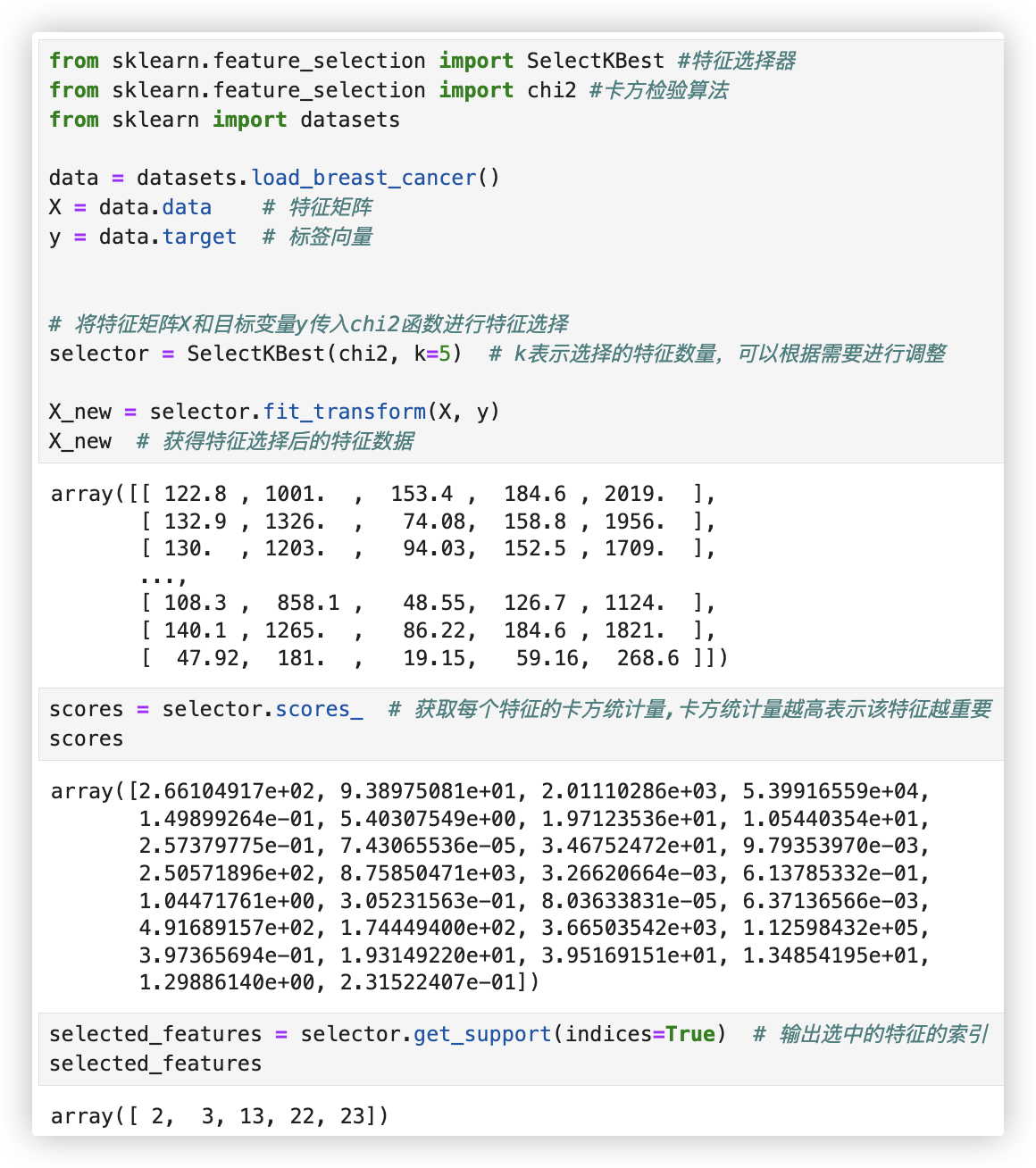
# 互信息