PyTorch的核心组件有4个, 这些核心组件构成了PyTorch进行深度学习的强大工具:

• 张量
• 自动求导模块
• 神经网络模块
• 优化器

---

张量Tensor

• PyTorch里面处理的最基本的操作对象就是Tensor, 它表示一个多维的矩阵.
• Pytorch的Tensor可以和numpy的ndarray相互转换.
  唯一不同的就是Pytorch的Tensor [可以] 在GPU上运行, 而numpy的ndarray [只能] 在cpu上运行.

Tensor常见的类型

(没有字符串类型,因为都是在做数值型运算)

• 浮点型

  • 单精度 torch.FloatTensor
  • 双精度 torch.DoubleTensor

• 整形

  • torch.ShortTensor (16位)
  • torch.IntTensor (32位)
  • torch.LongTensor (64位)

Tensor基本操作

以下的示例, 只是在抛砖引玉, 像numpy数组中的级联等操作,Tensor都能实现, 遇到了再查阅资料.. 无需面面俱到.
重点先记忆下 Tensor与numpy的转换, 以及 Tensor的变形操作..

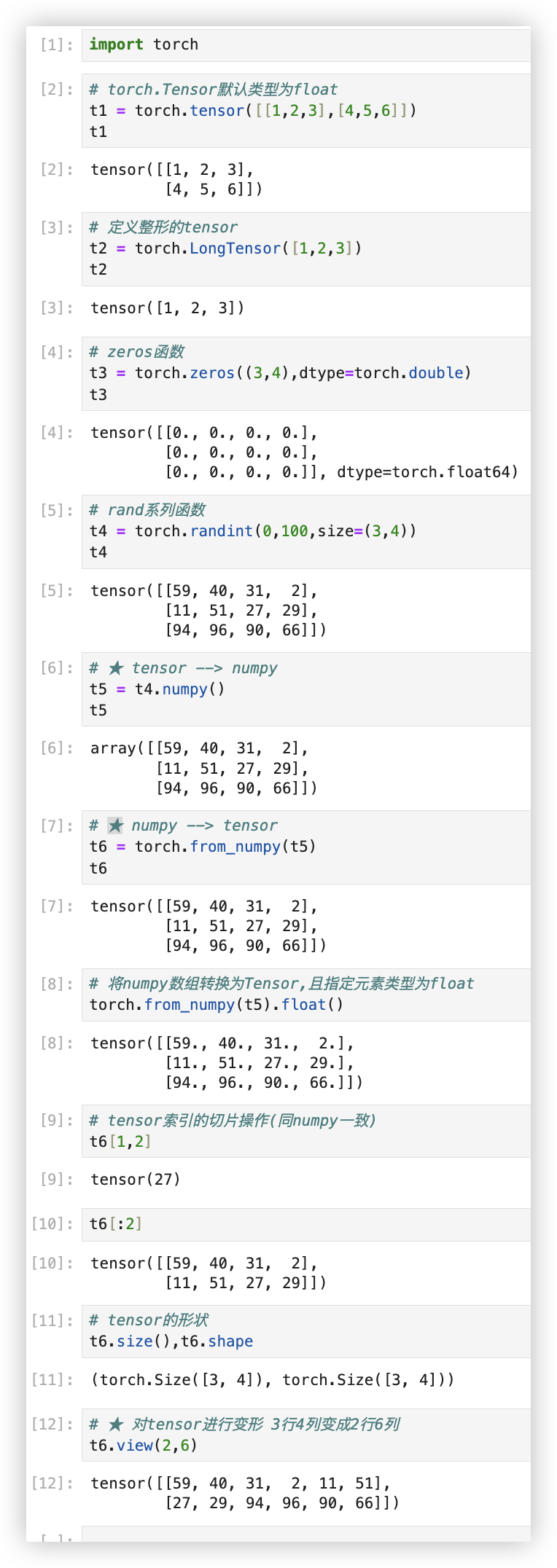
import torch

# torch.Tensor默认类型为float
t1 = torch.tensor([[1,2,3],[4,5,6]])
t1

# 定义整形的tensor
t2 = torch.LongTensor([1,2,3])
t2

# zeros函数
t3 = torch.zeros((3,4),dtype=torch.double)
t3

# rand系列函数
t4 = torch.randint(0,100,size=(3,4))
t4

# ★ tensor --> numpy
t5 = t4.numpy()
t5

# ★ numpy --> tensor 
t6 = torch.from_numpy(t5)
t6 

# 将numpy数组转换为Tensor,且指定元素类型为float
torch.from_numpy(t5).float()

# tensor索引的切片操作(同numpy一致)
t6[1,2]

t6[:2]

# tensor的形状
t6.size(),t6.shape

# ★ 对tensor进行变形 3行4列变成2行6列
t6.view(2,6)

Tensor GPU加速

目标: 基于Pytorch提供的GPU加速实现一组海量数据的运算.
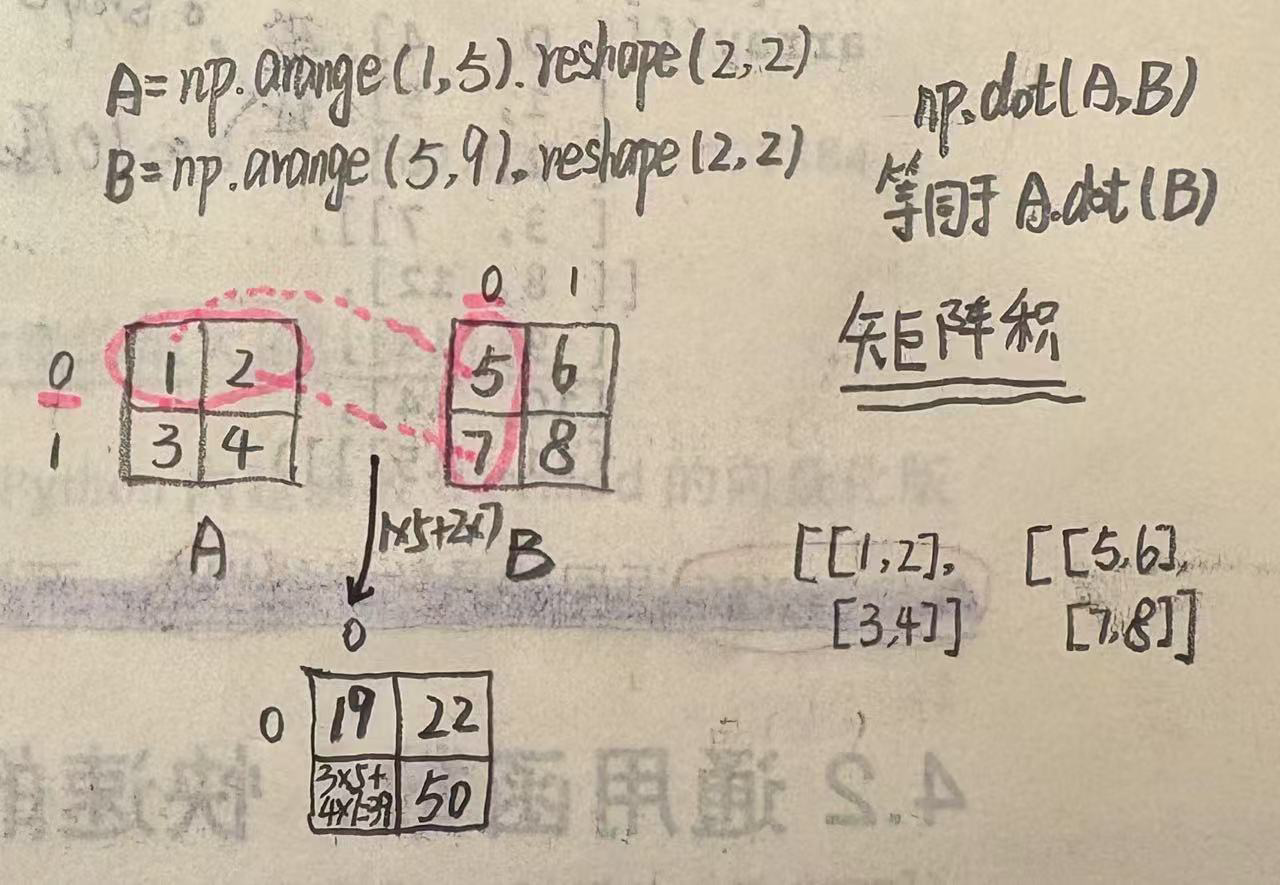
示例: 现有一个随机矩阵a形状是20000行2000列, 有一个随机矩阵b形状是2000行4000列. 要求对a和b两个矩阵进行矩阵相乘运算.

数据准备

import  torch
import  time

# 随机初始化两个矩阵
a = torch.randn(40000, 4000)
b = torch.randn(4000, 8000)

CPU执行耗时计算 - 2.3597571849823

t0 = time.time()
c = torch.matmul(a, b)
t1 = time.time()
print(t1 - t0, a.device, b.device)
"""
2.3597571849823 cpu cpu
"""

GPU执行耗时计算 - 0.0005350112915039062

# 将矩阵a和b扔到mps上进行GPU加速 window上是'cuda',mac上是'mps'
device = torch.device('mps')
a = a.to(device)
b = b.to(device)
print(a.device,b.device)
"""
mps:0 mps:0
"""

# 第一次GPU加速运算,会进行相关环境初始化工作(初始化工作只会进行一次,执行过后可删除该组代码)
t0 = time.time()
c = torch.matmul(a, b)
t2 = time.time()
print(t2 - t0)
"""
0.031223773956298828
"""

# 进行了环境初始化工作后,进行加速运算结果
t0 = time.time()
c = torch.matmul(a, b)
t2 = time.time()
print(t2 - t0)
"""
0.0005350112915039062
"""

---

自动求导模块

自动求导模块用于自动计算Tensor张量的梯度, 并在反向传播的过程中更新张量的值.
(即用张量来表示w权重,对其进行更新) 它是PyTorch中所有神经网络优化的基础.
通过使用autograd模块, 研究人员和开发人员可以专注于模型设计和业务逻辑, 而不需要编写复杂的梯度计算代码.

注意一点, 创建的变量要写在函数表达式之前.. 不然求偏导的结果是None.

autograd自动求导

函数 y = a**2 * x + b * x + c , 当x=1,a=1,b=2,c=3时, 分别求y对a求导、y对b求导和y对c求导的结果.
我们用代码 autograd自动求导 来实现. （简单理解,就是函数分别对a,b,c求偏导,三个偏导结果构成的向量就是梯度.
往梯度向量中代入x、a、b、c的值就是最终的结果）

import torch
from torch import autograd

x = torch.tensor(1.)
# requires_grad=True表示告诉oytorch框架将对该张量进行求导
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)

y = a**2 * x + b * x + c
# y分别对 添加了求导标识的 a、b、c进行求导
grads = autograd.grad(y, [a, b, c])
print('求导结果为:', grads[0], grads[1], grads[2])

"""
求导结果为: tensor(2.) tensor(1.) tensor(1.)
"""

backward自动求导

backward比autograd更强大一些, 不仅可以求导, 还可以进行参数更新..(参数更新在该示例中暂且不展示)
也就是说 backward反向传播,包含了求导这个功能..

在深度学习的训练过程中, backward()函数通过反向传播算法来计算损失函数关于模型参数的梯度/导数.

• 计算梯度: 根据损失函数对模型参数的依赖关系, 计算每个参数的梯度.
• 更新参数: 将计算出的梯度用于优化算法, 从而更新模型参数.
• 会有梯度累积的问题, 需手动清除梯度..

同样的,针对上面的示例,我们换个方式, 用代码 backward 自动求导 来实现. 函数 y = a**2 * x + b * x + c , 当x=1,a=1,b=2,c=3时, 分别求y对a求导、y对b求导和y对c求导的结果.

import torch

# 创建变量
x = torch.tensor(1.)  # x 不需要梯度
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)

# 定义计算表达式
y = a**2 * x + b * x + c

# 对 y 进行反向传播,计算 a、b、c 的梯度
y.backward()
# 查看 a、b、c 的梯度值
print('a 的梯度:', a.grad)  # dy/da
print('b 的梯度:', b.grad)  # dy/db
print('c 的梯度:', c.grad)  # dy/dc

"""
a 的梯度: tensor(2.)
b 的梯度: tensor(1.)
c 的梯度: tensor(1.)
"""

★敲黑板 - 梯度累积: 反向传播函数 backward()如果多次调用会发生梯度累积, 导致数据不准确;
避免梯度累积的解决方案: 每次调用backward函数之前,执行清除梯度的代码..

import torch

x = torch.tensor(1.)
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)

y = a**2 * x + b * x + c

for i in range(3):
   y.backward(retain_graph=True)
   print('a 的梯度:', a.grad)  # dy/da
   print('b 的梯度:', b.grad)  # dy/db
   print('c 的梯度:', c.grad)  # dy/dc

   # 通过下面运行输出,发现自动求导的结果(梯度)进行了累积
   # 为了避免这种问题的出现,通常需要我们在模型训练过程中,手动清除之前计算的梯度.
   # a.grad.zero_()
   # b.grad.zero_()
   # c.grad.zero_()
 
"""
a 的梯度: tensor(2.)
b 的梯度: tensor(1.)
c 的梯度: tensor(1.)
a 的梯度: tensor(4.)
b 的梯度: tensor(2.)
c 的梯度: tensor(2.)
a 的梯度: tensor(6.)
b 的梯度: tensor(3.)
c 的梯度: tensor(3.)
"""

Ps: 当然,也可以对一元函数进行求导,举个小例子

import torch

x = torch.tensor(2.0, requires_grad=True)
y = 3 * x ** 2 + 2 * x + 1  # f‘(x) = 6x + 2
y.backward()
print('打印梯度:', x.grad)  # 打印梯度: tensor(14.)

---

优化器

简单理解, 在传统机器学习中, 最小二乘、梯度下降就是优化器, 他们可以求的每个维度特征对应权重系数的最优值..
同样的, 在神经网络架构中, 优化器可以帮助我们得到 神经元上那些w的最优值..

学术一点, 优化器的主要作用是 自动调整模型参数, 以最小化损失函数.
在训练过程中, 优化器根据损失函数的梯度信息来更新模型参数, 从而逐步逼近最优解, 使得模型能够更好地拟合训练数据..

扫盲专区:
某个新闻报道,某个开源大模型有7500w个模型参数.
这里的7500w个不是指模型超参数的个数,而是指神经网络模型中那些神经元上那些w的个数!!

优化器的工作原理如下: (就是在前面"深度学习基础"章节,提及过的BP算法的过程)

• 前向传播: 将输入数据通过网络进行前向传播, 计算输出结果.
• 计算损失: 根据网络输出和真实标签计算损失函数的值.
• 反向传播: 通过反向传播算法计算损失函数关于每个参数的梯度.
• 更新参数: 使用优化器根据计算出的梯度来更新模型参数.

Pytorch提供了多种优化器的选择, 常用的优化器有: (前两个更常用)

	特点	适用场景	实现
SGD	简单且计算效率高, 适用于大多数情况	当数据集较大或需要快速迭代时, SGD梯度下降是一个不错的选择	torch.optim.SGD
Adam	结合了动量和自适应学习率的方法 对稀疏梯度和非平稳目标函数表现良好	适用于大多数深度学习任务 尤其是在处理非平稳目标函数时表现优异	torch.optim.Adam
RMSprop	通过调整每个参数的学习率 来适应不同的参数规模 适用于处理非平稳目标函数	适用于具有噪声的梯度 或需要不同学习率的场景	torch.optim.RMSprop
Adagrad	为每个参数分配不同的学习率 适用于稀疏数据	适用于特征维度非常高的稀疏数据	torch.optim.Adagrad

Q: 如何选择优化器?
(上述表格中的介绍看一眼就好),在真实的开发场景中,我们不会去探究训练过程中,是否是稀疏梯度、是否是非平稳目标函数等.
A: 都是直接莽, 这个优化器效果不好就换另一个优化器, 实践出真知.. 通过实验和调参, 找到最适合当前任务的优化器配置.
(神经网络层数多了,大神也没法用数学来论证为何某个优化器效果不好,机器学习本身就是玄学)

---

神经网络模块

数据准备

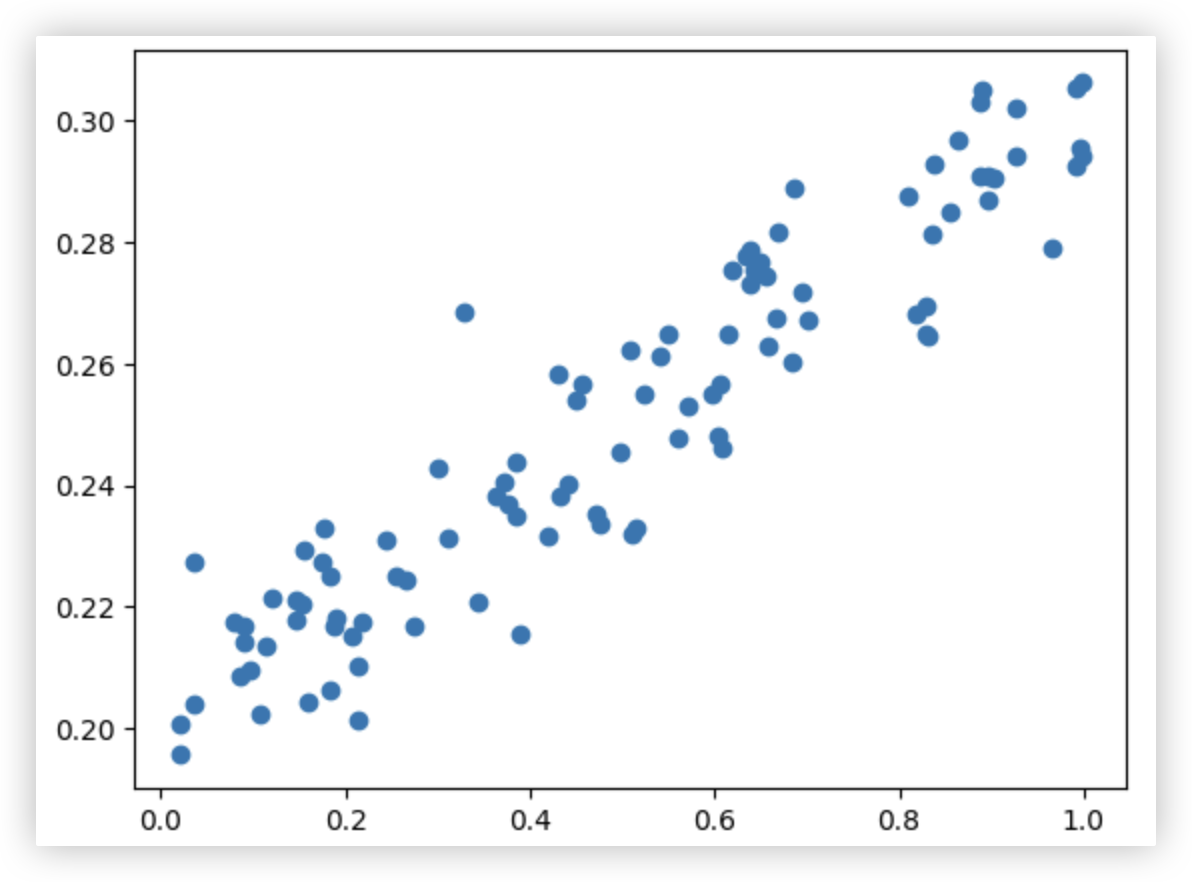
随机生成一堆数据, 需画一条线来对其进行拟合

import numpy as np
import matplotlib.pyplot as plt

# 特征矩阵x_data >> 使用numpy生成100个0到1之间的随机点,并转换成100行1列的二维数组
# 该特征矩阵只有一个特征维度!!
x_data = np.random.rand(100).reshape(-1, 1)

# 标签数据y_data >> 需添加一些随机扰动,不然散点图就是一条直线了.
noise = np.random.normal(0,0.01,x_data.shape) # 构建目标值,符合线性分布
y_data = x_data*0.1 + 0.2 + noise
y_data = y_data.reshape(-1, 1)

# 画散点图
plt.scatter(x_data, y_data)

简单回归的网络结构

构建一个最最简单的网络结构

需求: 需要对该数据集进行线性回归..(该数据集只有一个特征维度)
在此, 我们不用传统的机器学习画一条线来拟合这堆数据, 而是构建神经网络来拟合..

我们简单分析下:
针对这个简单的数据集,我们都不需要用隐层,单层网络架构就能解决<就"深度学习基础"章节中提及到的单层感知机>
1. 该数据集只有一个维度数据,则输入层只需一个神经元! 
2. 输出层也只需一个神经元!

虽然该网络结构很简单,很基础. 但神经网络的学习过程是绕不过BP算法的!
>> 即神经网络的学习过程由信号的正向传播和误差的反向传播两个过程组成.
   - 正向: 特征数据给输入层的神经元,给它匹配一个初始化的w,加权求和后给输出层的神经元,输出神经元再对其进行激活函数的处理
   - 误差: 将预测结果 与 真实标签进行误差计算 得到损失
   - 反向: 基于损失进行反向传播 进而更新w的权值!
   以上就是1次迭代训练的过程. 循环往复!有多少次迭代就更新多少次w!

★ 注意: 在下述过程中 没有进行数据集的切分,没有进行模型的评估.. 往后的学习中会完善这些内容.

构建网络结构

import torch.nn as nn

class LinearRegressionModel(nn.Module): # 基类nn.Module,后面会用到该类中的其他操作
    def __init__(self, input_dim, output_dim):
        """input_dim=1输入数据的维度/神经元个数,output_dim=1输出数据的维度"""
        super().__init__()
        # 构建网络结构,这里只有一层 <就像是单层感知机一样>
        self.linear = nn.Linear(input_dim, output_dim)  
        
    # 重写父类nn.Module中的forward方法,该方法用于实现向前传播
    def forward(self, x):
        """x是特征数据"""
        out = self.linear(x)
        return out

input_dim = 1   # 输入层1个神经元
output_dim = 1  # 输出层1个神经元

model = LinearRegressionModel(input_dim, output_dim)  # 创建网络结构
model
""" 这里的bias指的是截距b
LinearRegressionModel(
  (linear): Linear(in_features=1, out_features=1, bias=True)
)
"""

list(model.parameters())  # 可随机初始化得到一个w和b
"""
[Parameter containing: tensor([[0.5585]], requires_grad=True),
 Parameter containing: tensor([-0.4360], requires_grad=True)]
"""

网络结构训练

epochs = 2000         # 迭代训练周期
learning_rate = 0.01  # 学习率:用来调节权值变化的大小
# 定义优化器（这里选择梯度下降）> 需传入随机初始化的w和b
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()  # 因为是回归任务,我们用MSE作为损失函数

# 将特征和标签从numpy类型转型成float类型的张量tensor
inputs = torch.from_numpy(x_data).float()
labels = torch.from_numpy(y_data).float()

# 训练模型 - BP算法的过程
for epoch in range(1,epochs+1):
    # 因为backward函数进行反向传播求导,有梯度累积的问题.所以,每一次迭代前,梯度需要清零
    # 通过优化器来作梯度清零
    optimizer.zero_grad() 
    # - 前向传播
    outputs = model(inputs) # 实际上是在调用LinearRegressionModel类中的forward函数
    # - 计算损失 > 前向传播输出的预测值与真实标签进行对比
    loss = criterion(outputs, labels)
    # - 基于损失作反向传播,会计算梯度
    loss.backward()
    # - 更新权重参数 > 通过优化器来实现
    #   每一次迭代训练后,务必需要更新权重参数w(基于学习率和计算出来的梯度更新参数w)
    optimizer.step()
    # 每训练200次就打印一次训练日志
    if epoch % 200 == 0:
        print('epoch {}, loss {}'.format(epoch, loss.item()))
        
"""
epoch 200, loss 0.0013180893147364259
epoch 400, loss 0.0008123472216539085
epoch 600, loss 0.0005287033854983747
epoch 800, loss 0.00035336671862751245
epoch 1000, loss 0.00024498000857420266
epoch 1200, loss 0.00017797974578570575
epoch 1400, loss 0.00013656271039508283
epoch 1600, loss 0.00011096037633251399
epoch 1800, loss 9.51338151935488e-05
epoch 2000, loss 8.53505844133906e-05
"""

基于模型实现预测

作预测就是让模型作一次前向传播..

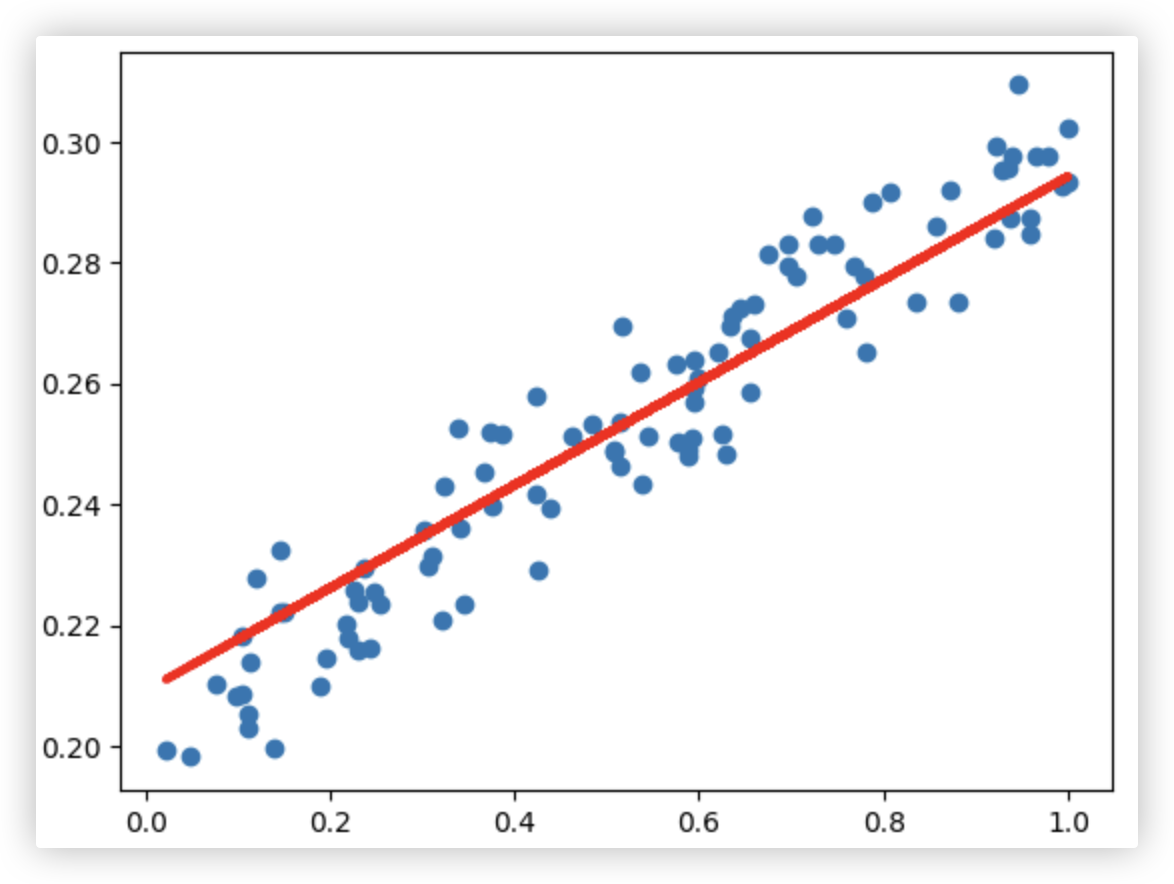
# 让最后的模型再前向传播下,得到预测值,因为画图需numpy类型,so,转下型
y_pred = model(inputs).data.numpy()  
plt.scatter(x_data,y_data)
plt.plot(x_data,y_pred,'r-',lw=3)

模型的保存与加载

注意: 这里保存的不是模型对象, 保存的是 模型的参数!!

model.state_dict()
"""
OrderedDict([('linear.weight', tensor([[0.0851]])),
             ('linear.bias', tensor([0.2091]))])
"""
# 保存
torch.save(model.state_dict(), 'model.pkl') 
# 加载 此处的model指的是创建好的网络架构
model.load_state_dict(torch.load('model.pkl'))
"""
<All keys matched successfully>
"""

题外话, 开源的大模型本地部署, 若下载的大模型有100个G. 这100个G存的就是模型的参数..
后续会讲解迁移学习、预训练模型后, 会对大模型的本质了解的更深刻..

---