 ★集成学习
★集成学习
集成学习Bagging算法 - 随机森林!!
集成学习Boosting算法 - Adaboost、GBDT.
# 分类随机森林
可用网格搜素的方式进行最优超参数的选取..
# 模型参数和使用
RandomForestClassifier
| 参数 | 含义 |
|---|---|
| n_estimators !! | 随机森林,子树的个数 默认是100 |
| Criterion | 不纯度衡量指标, 有基尼系数gini、信息熵entropy和MSE三种选择 默认是gini基尼系数 |
| max_depth | 单个树的最大深度, 超过深度的数值都会被剪掉 |
| min_samples_leaf | 一个节点在分支后每个子节点都必须包含的训练样本数 |
| min_samples_split | 一个节点想要分支必须要包含的训练样本数 |
| max_feature ◎ | 构建子树时, 每个节点随机选取 当前数据集合 中多少个特征进行 计算(eg:基尼系数的计算) |
| min_impurity_decrease | 信息增益小于该值的节点不会被分支 |
| bootstrap !!◎ | bootstrap就是用来控制抽样技术的参数. bootstrap参数默认True, 代表采用这种有放回的随机抽样技术. |
| oob_score !! | 该值为True, 则可以使用袋外数据测试模型. |
| random_state | 控制的是生成森林的模式, 类似决策树中的random_state, 用来固定森林中树的随机性. 当random_state固定时,随机森林中生成是一组固定的树。 |
PS: 表格中用 !! 标注的参数, 是 随机森林 相比于 决策树 独有的一些参数!
关于两个随机森林的两个随机: (样本随机和特征随机)
查阅源码注释,只知道bootstrap=True会采用 随机且放回的方案.. 那每次随机取多少条数据呢, 这个暂且不知道. 不纠结.
特征随机,相关的超参数就是 max_feature ..
# 单次在测试集中测试
树模型的优点是简单易懂, 可视化之后的树人人都能够看懂, 可惜随机森林是无法被可视化的. 为了更加直观地体会随机森林的效果, 我们来进行一个随机森林和单个决策树效益的对比. 我们使用红酒数据集:
from sklearn.tree import DecisionTreeClassifier # 决策树
from sklearn.ensemble import RandomForestClassifier # 随机森林
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
wine = load_wine()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = DecisionTreeClassifier()
rfc = RandomForestClassifier()
clf = clf.fit(Xtrain,Ytrain)
rfc = rfc.fit(Xtrain,Ytrain)
score_c = clf.score(Xtest,Ytest)
score_r = rfc.score(Xtest,Ytest)
print(score_c,score_r) # 0.9074074074074074 0.9629629629629629
2
3
4
5
6
7
8
9
10
11
12
13
14
每次运行,结果都不一样,但都是随机森林的结果比决策树的好.. 之所以会变是因为随机性的存在(决策树中有、随机森林中也有) !!
# 一组交叉验证测试
我们基于一组交叉验证进行测试比对!!
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
rfc = RandomForestClassifier(n_estimators=25)
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10)
clf = DecisionTreeClassifier()
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10)
plt.plot(range(1,11),rfc_s,label = "RandomForest")
plt.plot(range(1,11),clf_s,label = "Decision Tree")
plt.legend()
plt.show()
rfc_s.mean(),clf_s.mean() # (0.9833333333333334, 0.8539215686274509)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
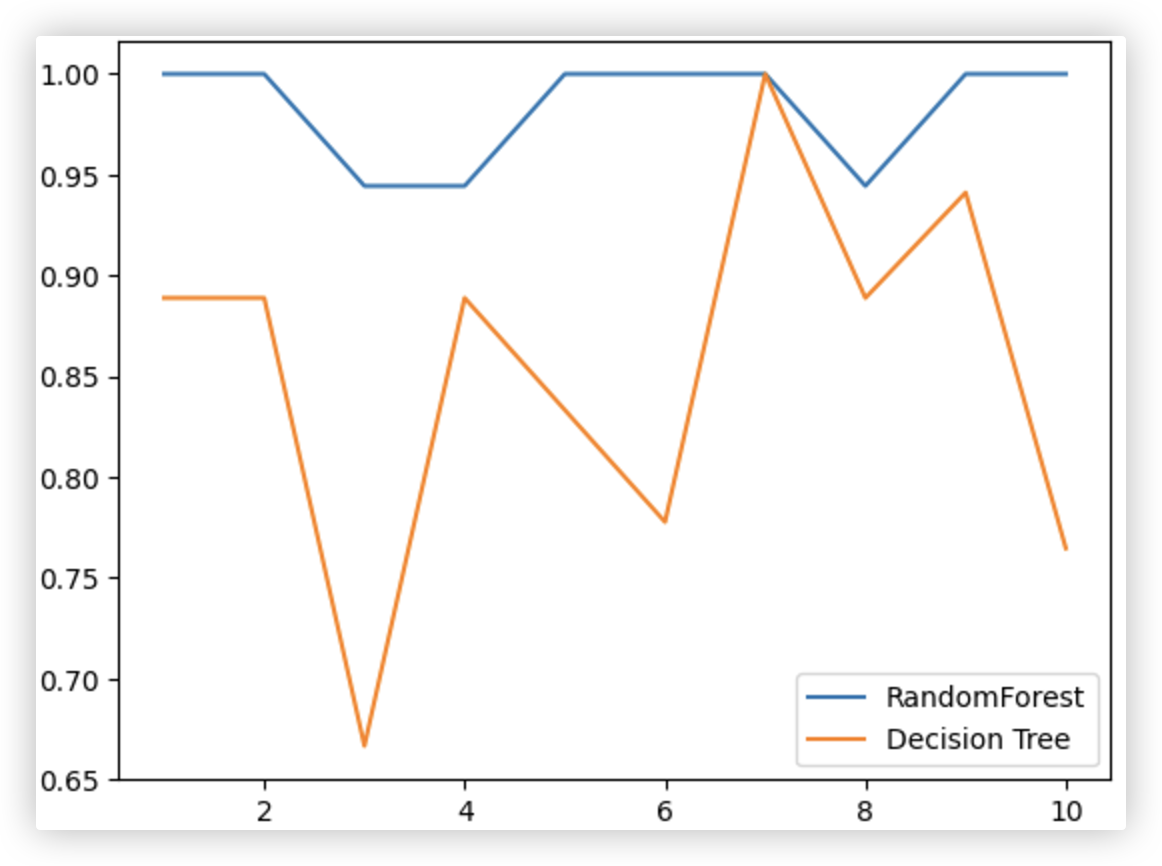
随着折数的增加,随机森林评分的结果相对是比较平缓的.决策树的出入会比较大;
从整体上来看,随机森林交叉验证的结果是要好于决策树的!
# 多组交叉验证测试
仅一组交叉验证的结果也可能有偶然性的发生, 那我们加大交叉验证的次数.
循环10组交叉验证,每组交叉验证都是10折,取每组10折的均值
rfc_l = []
clf_l = []
for i in range(10):
rfc = RandomForestClassifier(n_estimators=25)
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
rfc_l.append(rfc_s)
clf = DecisionTreeClassifier()
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()
clf_l.append(clf_s)
plt.plot(range(1,11),rfc_l,label = "Random Forest")
plt.plot(range(1,11),clf_l,label = "Decision Tree")
plt.legend()
plt.show()
2
3
4
5
6
7
8
9
10
11
12
13
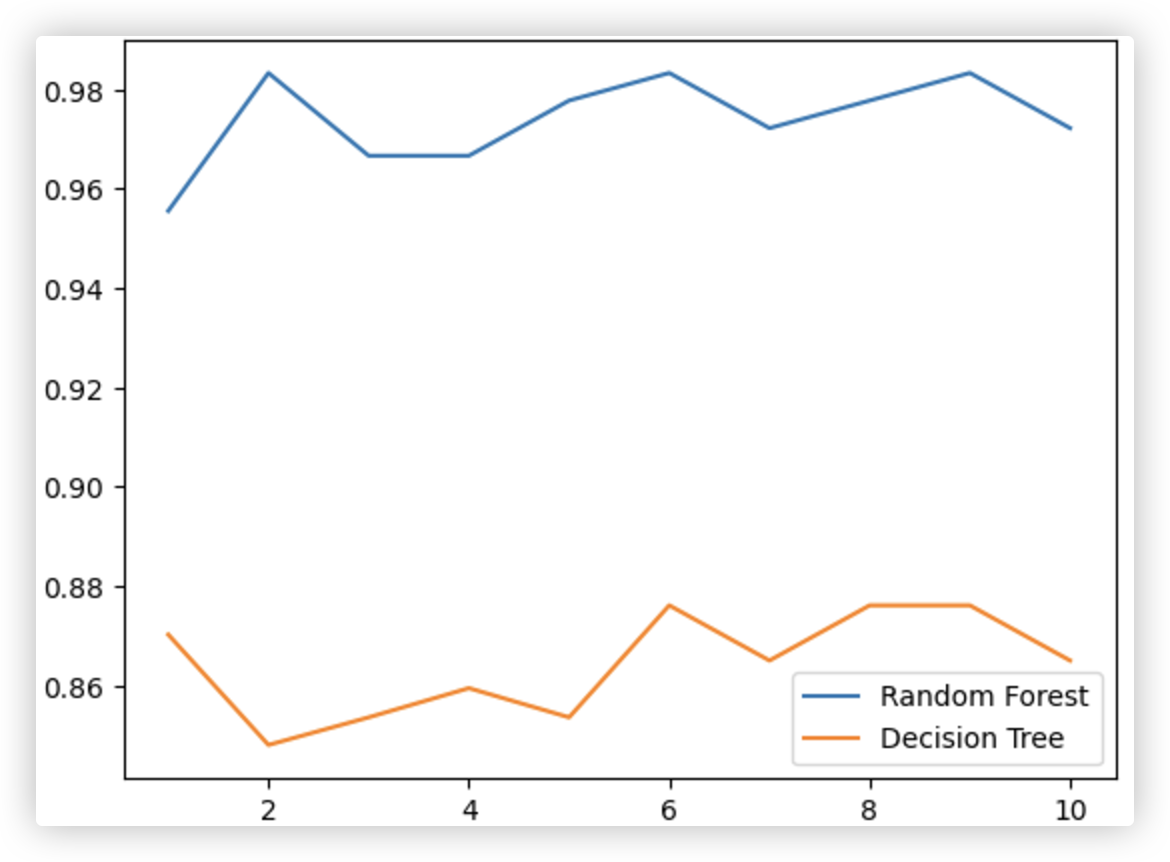
可以感受到,随机森林在各个方面都要比决策树效果要好!!
# 使用袋外数据进行测试
"""
随机森林使用袋外数据评价模型
- 有放回抽样也会有自己的问题.
由于是有放回,一些样本可能会被采集多次,而其他一些样本却可能被忽略,一次都未被采集到.
那么这些被忽略或者一次都没被采集到的样本叫做oob袋外数据!!
- 也就是说,在使用随机森林时,我们可以不划分测试集和训练集,只需要用袋外数据来测试我们的模型即可!
- 如果希望用袋外数据来测试,则需要在实例化时就将oob_score这个参数调整为True.
训练完毕之后,我们可以用随机森林的另一个重要属性:oob_score_ 来查看我们的在袋外数据上测试的结果.
"""
from sklearn.ensemble import RandomForestClassifier # 随机森林
from sklearn.datasets import load_wine
feature = load_wine().data
target = load_wine().target
model = RandomForestClassifier(n_estimators=100,oob_score=True)
model.fit(feature,target)
model.oob_score_ # 使用袋外数据对模型进行测试的结果 0.9887640449438202
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 回归随机森林
# 模型参数和使用
RandomForestRegression
- 回归随机森林模型所有的参数, 属性与接口, 全部和分类随机森林一致. 仅有的不同就是回归树与分类树衡量不纯度的指标不同, 也就是参数Criterion不一致!
- Criterion参数:
- 回归树衡量分枝质量的指标, 支持的标准有2种:
- 输入"mse" 使用均方误差mean squared error(MSE)
父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准,差值越小不纯度越低 - 输入"friedman_mse"使用费尔德曼均方误差, 这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
- 输入"mse" 使用均方误差mean squared error(MSE)
- 回归树衡量分枝质量的指标, 支持的标准有2种:
# 作缺失值预测
使用案例: 使用回归随机森林 [预测] 样本中的 [缺失值] 数据 (示例使用的是 信贷业务相关的数据集
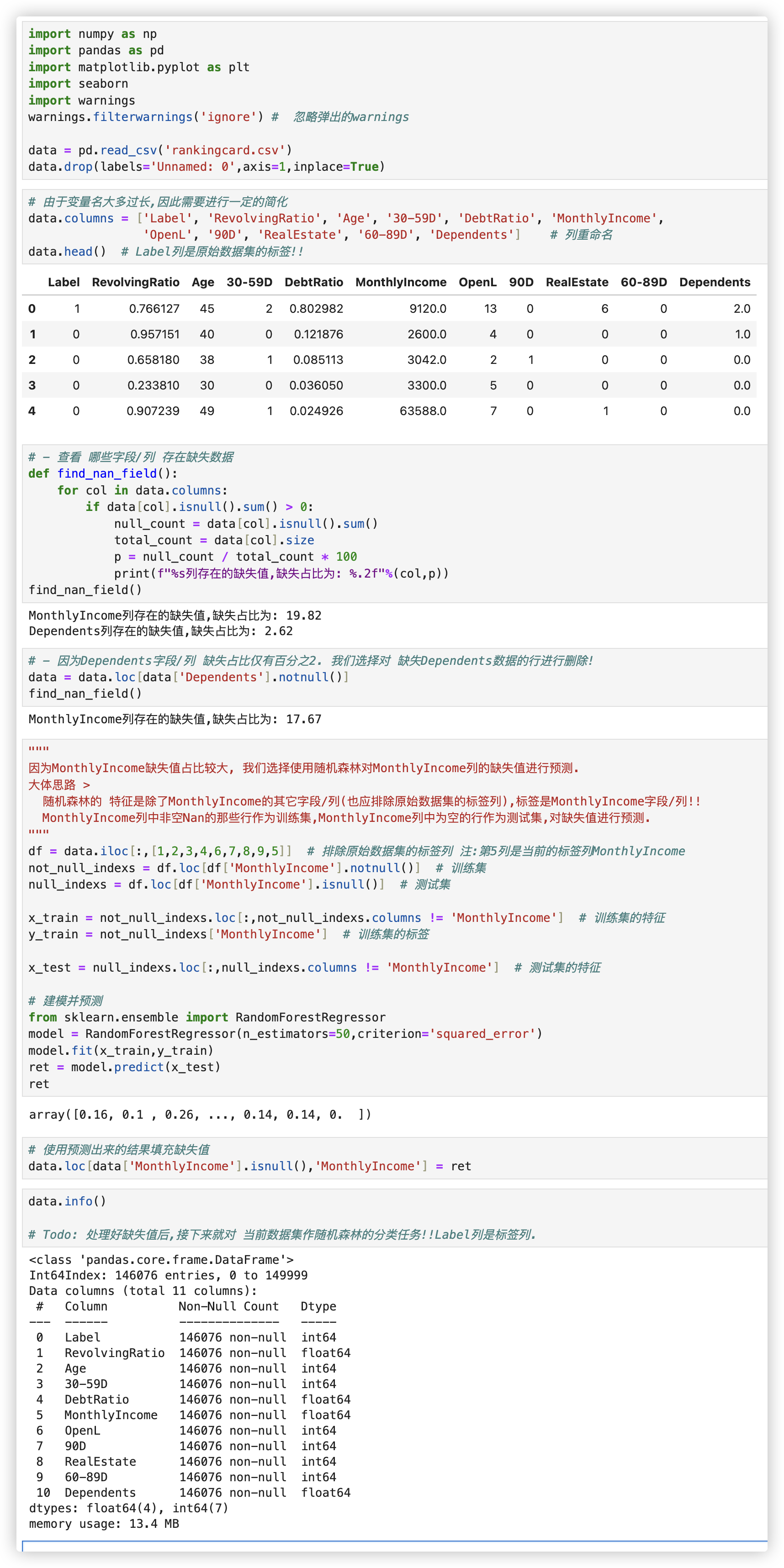
代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn
import warnings
warnings.filterwarnings('ignore') # 忽略弹出的warnings
data = pd.read_csv('rankingcard.csv')
data.drop(labels='Unnamed: 0',axis=1,inplace=True)
# 由于变量名大多过长,因此需要进行一定的简化
data.columns = ['Label', 'RevolvingRatio', 'Age', '30-59D', 'DebtRatio', 'MonthlyIncome',
'OpenL', '90D', 'RealEstate', '60-89D', 'Dependents'] # 列重命名
data.head() # Label列是原始数据集的标签!!
# - 查看 哪些字段/列 存在缺失数据
# df.isnull().sum() / df.shape[0] 也可以查看相关数据!
def find_nan_field():
for col in data.columns:
if data[col].isnull().sum() > 0:
null_count = data[col].isnull().sum()
total_count = data[col].size
p = null_count / total_count * 100
print(f"%s列存在的缺失值,缺失占比为: %.2f"%(col,p))
find_nan_field()
# - 因为Dependents字段/列 缺失占比仅有百分之2. 我们选择对 缺失Dependents数据的行进行删除!
data = data.loc[data['Dependents'].notnull()]
find_nan_field()
"""
因为MonthlyIncome缺失值占比较大, 我们选择使用随机森林对MonthlyIncome列的缺失值进行预测.
大体思路 >
随机森林的 特征是除了MonthlyIncome的其它字段/列(也应排除原始数据集的标签列),标签是MonthlyIncome字段/列!!
MonthlyIncome列中非空Nan的那些行作为训练集,MonthlyIncome列中为空的行作为测试集,对缺失值进行预测.
"""
# df1 = data.iloc[:,[1,2,3,4,5,6,7,8,9,10]] df2 = data.iloc[:,data.columns != 'Label']
# df1和df2是一模一样的!!
df = data.iloc[:,[1,2,3,4,6,7,8,9,5]] # 排除原始数据集的标签列 注:第5列是当前的标签列MonthlyIncome
not_null_indexs = df.loc[df['MonthlyIncome'].notnull()] # 训练集 等同于df[df['MonthlyIncome'].notnull()]
null_indexs = df.loc[df['MonthlyIncome'].isnull()] # 测试集
x_train = not_null_indexs.loc[:,not_null_indexs.columns != 'MonthlyIncome'] # 训练集的特征 矩阵
y_train = not_null_indexs['MonthlyIncome'] # 训练集的标签 列
x_test = null_indexs.loc[:,null_indexs.columns != 'MonthlyIncome'] # 测试集的特征 矩阵
# 建模并预测
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=50,criterion='squared_error')
model.fit(x_train,y_train)
ret = model.predict(x_test)
ret
# 使用预测出来的结果填充缺失值
data.loc[data['MonthlyIncome'].isnull(),'MonthlyIncome'] = ret
data.info()
# Todo: 处理好缺失值后,接下来就对 当前数据集作随机森林的分类任务!!Label列是标签列.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 随机森林 - 离职分析项目
项目背景:
在人力资源管理领域中, 分析各项员工工作相关的数据和指标.
可以揭示员工流失的趋势和原因、薪酬公平性、员工满意度以及职业发展路径等关键指标.
这些见解对于优化人才招聘、留存策略、绩效评估体系和员工发展计划至关重要..
本项目主要针对员工流失情况来进行分析, 并且建立了随机森林模型来探究员工流失的重要因素.
还能预测员工是否存在离职的可能, 有助于帮助公司提前与该员工沟通, 并且及时作出战略性调整!
# 表格字段信息
| EmpID | 唯一的员工ID
| Age | 1年龄
| AgeGroup | 年龄组
| Attrition | 是否离职
| BusinessTravel | 2出差: 很少、频繁、不出差
| DailyRate | 日薪
| Department | 2任职部门: 研发部门、销售部门、人力资源部门
| DistanceFromHome | 2通勤距离
| Education | 1教育等级
| EducationField | 1专业领域: 生命科学、医学、市场营销、技术、其他
| EnvironmentSatisfaction | 3工作环境满意度
| Gender | 1性别
| HourlyRate | 时薪
| JobInvolvement | 2工作参与度
| JobLevel | 2工作级别
| JobRole | 2工作角色
| JobSatisfaction | 3工作满意度
| MaritalStatus | 1婚姻状况
| MonthlyIncome | 2月收入
| SalarySlab | 工资单
| MonthlyRate | 月薪
| NumCompaniesWorked | 工作过的公司数量
| PercentSalaryHike | 4加薪百分比
| PerformanceRating | 4绩效评级
| RelationshipSatisfaction| 3关系满意度
| StandardHours | 标准工时
| StockOptionLevel | 4股票期权级别
| TotalWorkingYears | 总工作年数
| TrainingTimesLastYear | 4去年培训时间
| WorkLifeBalance | 3工作生活平衡评价
| YearsAtCompany | 5在公司工作年数
| YearsInCurrentRole | 5担任现职年数
| YearsSinceLastPromotion | 5上次晋升后的年数
| YearsWithCurrManager | 5与现任经理共事年数
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
step1: 先作数据清洗/预处理
step2: 在处理字段时.. 可以先了解每个字段的含义, 并对它们进行初步分类. 例如:
员工个人情况字段 - 年龄、婚姻状况、性别、教育等级和专业领域/背景
工作方面字段包括 - 出差、部门、通勤距离、工作角色、工作参与度、工作级别和月收入
评分方面字段包括 - 工作环境满意度、工作满意度、关系满意度、工作生活平衡评价
薪酬方面字段包括 - 加薪百分比、绩效评级、股票期权级别、去年培训时间
晋升方面字段包括 - 在公司工作年数、担任现职年数、上次晋升后的年数、与现任经理共事年数
2
3
4
5
- step3: 接着对每一部分的字段进行探索, 按照以下步骤进行分析:
- 字段类型判断: 确定每个字段是连续型 (数值型) 还是离散型 (类别型).
- 对于连续型字段, 可以查看其统计特性 (如均值、中位数、标准差等) - 箱型图.
- 对于离散型字段, 需要查看其唯一值及组成元素, 并分析其分布情况 (例如,各类别的频率) - 柱状图.
- 特征与结果的关系分析
- 使用可视化工具 (如柱状图、箱线图、散点图等) 查看每个字段与目标结果之间的关系. 这有助于发现潜在的相关性或模式.
- 字段类型判断: 确定每个字段是连续型 (数值型) 还是离散型 (类别型).
通过上述这些步骤, 不仅能够全面了解数据特征, 还可以对特征的重要性和可用性作出初步判断.
即可以 [适当] 的人为的进行一些特征选择, 不让某些字段参与建模, 这样模型运算的压力就会小一些..
(每个字段与是否离职作相关性分析 / 字段与是否离职是否存在某种形式的关联)
# 数据预处理
其实就是老生常谈的几部曲,这几个预处理步骤是具有通用性的,代码解释详见 以往关于pandas的总结!
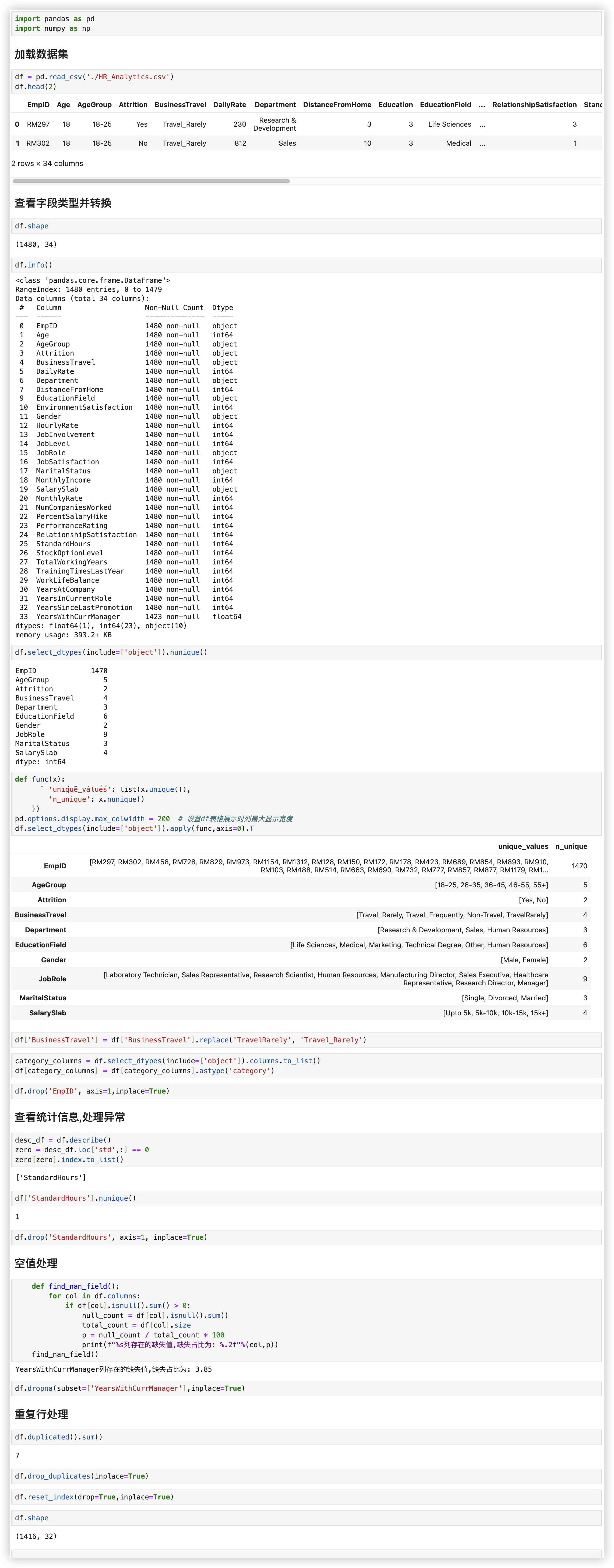
# 离职情况分析
即 每个字段与是否离职作相关性分析 / 字段与是否离职是否存在某种形式的关联!!
注意
AgeGroup字段、Attrition字段都是离散型数据
- AgeGroup字段 > 18-25, 26-35, 36-45, 46-55, 55+
- Attrition字段 > Yes, No
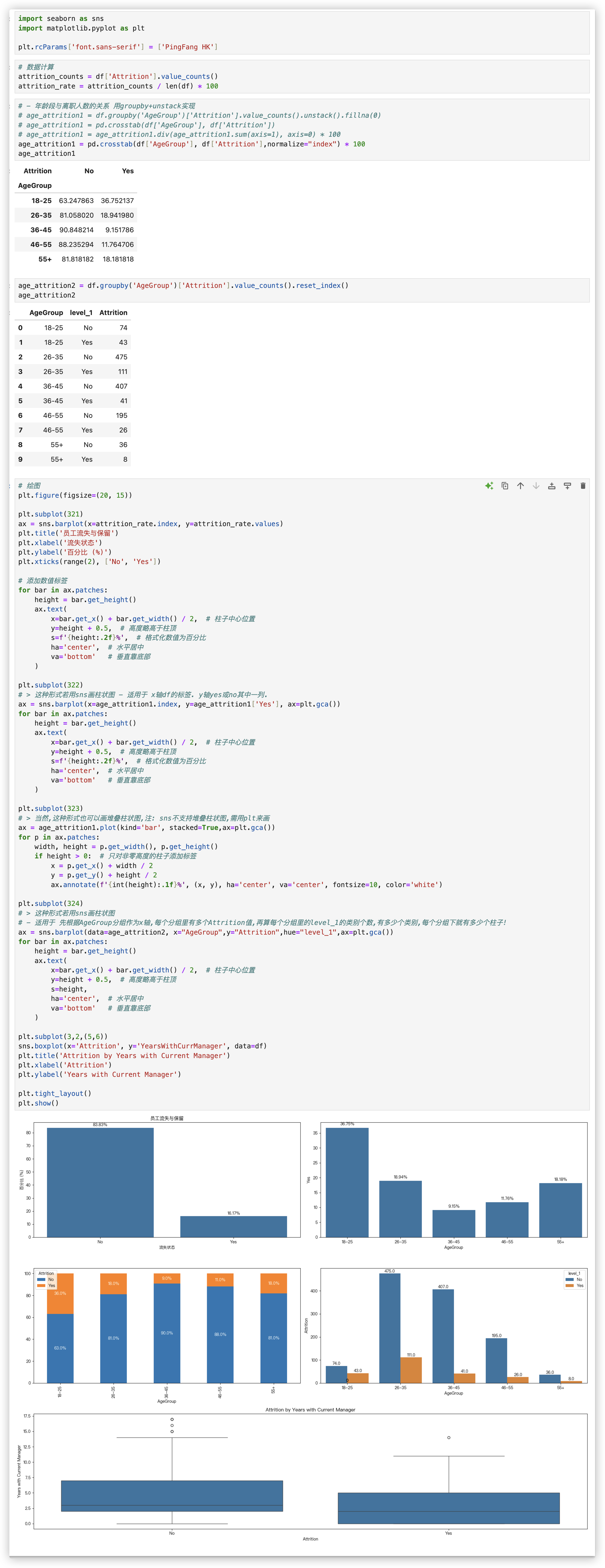
第一个子图是 - 观察attrition_rate的结构
Attrition离散型特征的每个类别 比例的柱状图
第二个子图是 - age_attrition1
AgeGroup和Attrition 两个离散型特征的类别交叉, x轴是AgeGroup的全部类别,柱子上只是Attrition的其中一个类别
第三个子图是 - age_attrition1
是堆叠的柱状图 x轴是AgeGroup的全部类别,柱子上堆叠的是Attrition的全部类别
第四个子图是 - age_attrition2
x轴是AgeGroup的全部类别,AgeGroup的每个类别都对应多根柱子,这些柱子对应Attrition的全部类别
第五个子图是 箱型图!!
每个柱状图类型的子图,写标题,给柱子添加文字标签的代码都是差不多的!!!
plt.title('员工流失与保留')
plt.xlabel('流失状态')
plt.ylabel('百分比 (%)')
plt.xticks(range(2), ['No', 'Yes'])
# 添加数值标签
for bar in ax.patches:
height = bar.get_height()
ax.text(
x=bar.get_x() + bar.get_width() / 2, # 柱子中心位置
y=height + 0.5, # 高度略高于柱顶
s=f'{height:.2f}%', # 格式化数值为百分比
ha='center', # 水平居中
va='bottom' # 垂直靠底部
)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 建模
# 特征初步筛选
根据上面的离职情况分析, 对特征作个初步筛选, 然后将 离散型特征 进行 标签编码.
features = ['Age', 'BusinessTravel', 'Department', 'Education', 'EducationField',
'EnvironmentSatisfaction', 'Gender', 'JobInvolvement', 'JobLevel',
'JobSatisfaction', 'MaritalStatus', 'MonthlyIncome', 'RelationshipSatisfaction',
'WorkLifeBalance', 'YearsAtCompany', 'YearsInCurrentRole',
'YearsSinceLastPromotion', 'YearsWithCurrManager','Attrition']
new_data = data[features]
# 编码原则: 1-3个 map映射; 3个以上 使用one-hot编码!!
new_data['BusinessTravel'] = new_data['BusinessTravel'].map({
'Non-Travel': 0,
'Travel_Rarely': 1,
'Travel_Frequently': 2
})
new_data['Gender'] = new_data['Gender'].map({
'Female': 0,
'Male': 1
})
new_data['MaritalStatus'] = new_data['MaritalStatus'].map({
'Divorced': -1,
'Single': 0,
'Married': 1
})
new_data['Attrition'] = new_data['Attrition'].map({
'Yes': 1,
'No': 0
})
new_data.reset_index(drop=True, inplace=True)
result1 = pd.get_dummies(new_data['Department'])
result2 = pd.get_dummies(new_data['EducationField'])
new_data = pd.concat((new_data,result1),axis=1).drop(columns='Department')
new_data = pd.concat((new_data,result2),axis=1).drop(columns='EducationField')
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 建立模型
x = new_data.drop('Attrition', axis=1)
y = new_data['Attrition']
# 采用分层抽样来保证训练集和测试集中label与整体数据集的label分布相似
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=10) # 37分
rf_clf = RandomForestClassifier()
rf_clf.fit(x_train, y_train)
2
3
4
5
6
7
# 模型评估
from sklearn.metrics import f1_score
y_pred_rf = rf_clf.predict(x_test)
class_report_rf = classification_report(y_test, y_pred_rf)
print(class_report_rf)
"""
precision recall f1-score support > 精确率、召回率、F1-score
0 0.89 0.98 0.93 385
1 0.55 0.19 0.28 59
accuracy 0.87 444 > 准确率
macro avg 0.72 0.58 0.60 444
weighted avg 0.84 0.87 0.84 444
>> 类别1的三个指标precision,recall,f1-score差别很大,是因为样本分布是不均匀的!!
可通过 y.value_counts()验证!
0 1242
1 238
Name: Attrition, dtype: int64
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 模型优化
建议写个循环,5次到10次.把每次的模型对象存起来.. 看哪次的最好!!
因为每次网格搜索因为随机的原因,得到的最优参数都是不一样的.
# 网格搜索的过程是个漫长的过程 每个超参数的范围大一点时间就是数量级的
param_grid = {
'n_estimators':np.arange(10,50,5), # 决策树的数量,数值越大,模型可能越好,但是也能会导致过拟合
'max_depth':np.arange(5,20,2), # 决策树的最大深度,控制模型的复杂度
'min_samples_split':np.arange(1,10,2), # 决定节点分裂的最小样本数量
'min_samples_leaf':np.arange(1,10,2), # 决定叶节点的最小样本数量
'max_features':['auto','sqrt','log2'] # 考虑分裂时的特征数量
}
rf = RandomForestClassifier()
# ★ n_jobs=-1 会使网格搜索快些,因为它会调用全部的cpu进行网格搜索
grid_search = GridSearchCV(estimator=rf,param_grid=param_grid,cv=5,n_jobs=-1)
grid_search.fit(x_train,y_train)
print('Best parameters found:',grid_search.best_params_)
"""
Best parameters found:
{'max_depth': 7, 'max_features': 'log2', 'min_samples_leaf': 1, 'min_samples_split': 3, 'n_estimators': 35}
"""
best_rf = grid_search.best_estimator_ # 拿到最好的参数对应的模型对象
y_pred_orf = best_rf.predict(x_test)
class_report_orf = classification_report(y_test, y_pred_orf)
print(class_report_orf)
"""
precision recall f1-score support
0 0.88 0.99 0.93 385
1 0.64 0.15 0.25 59
accuracy 0.88 444
macro avg 0.76 0.57 0.59 444
weighted avg 0.85 0.88 0.84 444
"""
# > 相比未优化的随机森林模型,性能有所提升,但是各项评分提升的不大,这意味着模型的总体区分能力在优化后并没有显著提升.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 重要特征
rf_feature_importance = best_rf.feature_importances_
feature_names = x_train.columns
rf_feature_df = pd.DataFrame({
'Feature': feature_names,
'Importance': rf_feature_importance
})
# 筛选出前五的重要特征
sorted_rf_feature_df = rf_feature_df.sort_values(by='Importance', ascending=False).head()
sorted_rf_feature_df
"""
Feature Importance
9 MonthlyIncome 0.134731
0 Age 0.119173
12 YearsAtCompany 0.097644
15 YearsWithCurrManager 0.064445
13 YearsInCurrentRole 0.058102
"""
# 在随机森林模型中,重要程度最大的是: 月收入>年龄>在公司工作年数>担任现职年数>与现任经理共事年数.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 结论
本项目主要针对离职率进行了探索,得出了以下结论:
1.基于员工个人情况,离职情况主要集中在18-35岁的员工群体中,随着年龄增长,离职的人数有所下降.
男性的离职率略高于女性的离职率,学历等级1-3级的离职率最高,人力资源专业、市场营销专业、技术专业离职率最高.
2.基于员工工作情况,经常出差的员工离职率高;人力资源部门和销售部门的离职率比研发部门高;
离职的员工离职员工的通勤距离中位数略高于未离职员工;
销售代表、人力资源和实验室技术员的离职率比较高,研究总监、经理和制造总监的离职率较低;
工作参与度越低的员工离职率越高;工作等级位于1级和3级的离职率比较高.
离职员工的月收入中位数明显低于未离职员工,且未离职员工的月收入分布范围更广,尤其是在较高收入区间.
3.评分方面,随着工作环境满意度、工作满意度的提高,离职员工的比例逐渐减少;
关系满意度、工作生活平衡评价给出1级的员工离职率最高,给出4级的比2、3级的离职率高,可能是因为这部分人工作上的参与度比较低.
4.薪酬方面,离职员工加薪百分比中位数明显低于未离职员工;绩效评级只有3级和4级,离职率看起来与绩效评级的关系并不大;
股票期权级别越高,越不容易离职;去年培训时间看起来与离职率的关系并不算大.
5.晋升方面,较短的在公司工作年数可能与较高的离职率相关联,这表明新员工可能更倾向于离职;
在当前职位上工作时间较短的员工可能更容易离职,这可能反映了对工作的不满或晋升机会的缺乏;
较长时间没有晋升的员工可能更倾向于离职(离职员工中位数略高于未离职员工),这可能是由于缺乏职业成长或晋升机会;
与现任经理共事时间较短的员工可能更容易离职.
6.通过建立随机森林模型,不仅可以得出影响离职最大的因素,还能预测哪些员工可能会离职,可以提前进行沟通疏导.
特征重要程度: 月收入>年龄>在公司工作年数>担任现职年数>与现任经理共事年数.
>> 建议:
1.建议减少出差情况,或者对经常出差的员工给予一些福利,留住这一类员工.
2.适当提高人力资源部门和销售部门的福利,留住这两个部门的员工.
3.提高3级学历员工的薪酬待遇,留住中高人才.
4.可以提高员工的工作参与度,有助于他们留在公司.
5.对于年轻的员工更要给予帮助,有助于留住年轻人才.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Adaboost
from sklearn.ensemble import AdaBoostClassifier
模型超参数
- n_estimators: 迭代次数/弱评估器的数量
- 这个参数表示要执行的迭代次数, 也就是要训练的弱分类器的数量. 默认值为50.
增加迭代次数可以提高模型的性能, 但也会增加训练时间.
- 这个参数表示要执行的迭代次数, 也就是要训练的弱分类器的数量. 默认值为50.
- base_estimator: 弱分类器
- 这个参数指定了要使用的基本分类器. 也就是弱分类器的类型.
可以选择的基本分类器包括决策树、支持向量机等, 默认为分类决策树.
- 这个参数指定了要使用的基本分类器. 也就是弱分类器的类型.
- learning_rate: 学习率
- 学习率控制每个弱分类器的权重调整幅度.
较小的学习率可以使权重调整更加温和, 较大的学习率可以使权重调整更加剧烈. 默认值为1.0
- 学习率控制每个弱分类器的权重调整幅度.
- algorithm: 算法
- 这个参数指定了用于计算样本权值的算法.
可以选择的算法有SAMME和SAMME.R. 默认为SAMME.R, 它基于对样本权值进行概率估计进行加权.
- 这个参数指定了用于计算样本权值的算法.
- random_state: 随机种子
- 设置相同的随机种子可以使每次运行的结果保持一致
这些超参数可以根据具体的问题和数据集进行调节.
一般来说, 增加迭代次数和降低学习率可以提高模型的性能, 但也会增加训练时间.
选择合适的基本分类器和算法也可以影响模型的性能.
AdaBoostClassifier在二分类任务处理中,要比随机森林和决策树要好
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier # 分类决策树
from sklearn.ensemble import RandomForestClassifier # 分类随机森林
from sklearn.ensemble import AdaBoostClassifier # AdaBoost
from sklearn import datasets
from sklearn.model_selection import cross_val_score # 交叉验证
X,y = datasets.load_breast_cancer(return_X_y=True) # 乳腺癌二分类数据集
pd.Series(y).value_counts()
"""
1 357
0 212
dtype: int64
"""
score = 0
for i in range(10):
model = DecisionTreeClassifier()
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
score = 0
for i in range(10):
model = RandomForestClassifier()
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
score = 0
for i in range(10):
model = AdaBoostClassifier(algorithm='SAMME')
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
"""
0.9191150442477876
0.961361589815246
0.9676727216270764
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
AdaBoostClassifier不适合用作在多分类中
X,y = datasets.load_digits(return_X_y=True) # 手写数字
pd.Series(y).value_counts()
"""
3 183
1 182
5 182
4 181
6 181
9 180
7 179
0 178
2 177
8 174
dtype: int64
"""
score = 0
for i in range(10):
model = DecisionTreeClassifier()
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
score = 0
for i in range(10):
model = RandomForestClassifier()
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
score = 0
for i in range(10):
model = AdaBoostClassifier(algorithm='SAMME')
score += cross_val_score(model,X,y,cv=5).mean()
print(score / 10)
"""
0.7840713401423708
0.9382505416279792
0.7051238006809036
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# GBDT
sklearn.ensemble.GradientBoostingClassifier()
sklearn.ensemble.GradientBoostingRegressor()
# 模型参数
- n_estimators和learning_rate 跟 Adaboost的一样.
- init 用于初始预测结果H0的设置, 是跟那个加法模型/加权多数表决相关的.
该参数不是很重要, 一般在GBDT的使用过程中, 不会去主动设置它, 保持默认值就行.
当我们有足够的算力支持超参数搜索时, 我们可以在 init 这个参数值上进行选择. - subsamples 用于指定每个基础决策树构建过程中使用的样本数量的比例
- 如果subsamples参数设置为小于1的浮点数, 比如0.8
表示每个弱评估器的训练样本是原始样本的一个随机子集, 且子集的大小是原始样本大小乘以subsamples参数.
这种随机采样方式可以用于减少过拟合的风险, 增加模型的泛化能力. - 如果subsamples参数设置为大于等于1的整数, 比如100.
表示每个弱评估器的训练样本是原始样本的一个随机子集.且子集的大小是subsamples参数指定的数值
这种随机采样方式可以用于降低计算复杂度和训练时间, 特别是当样本数量非常大时.
- 如果subsamples参数设置为小于1的浮点数, 比如0.8
- loss 选择GBDT的损失函数.
- 分类器中的
loss: 字符串型, 可输入"deviance", "exponential", 默认值="deviance"
其中"deviance"直译为偏差, 特指逻辑回归的损失函数 -- 交叉熵损失
而"exponential"则特指AdaBoost中使用的指数损失函数. - 回归器中的
loss: 字符串型, 可输入{"squared_error", "absolute_error", "huber", "quantile"}, 默认值="squared_error"
其中'squared_error'是指回归的平方误差, 'absolute_error'指的是回归的绝对误差, 'huber'是以上两者的结合.
'quantile'则表示使用分位数回归中的弹球损失.
- 分类器中的
Q: 如何选择不同的损失函数?
GBDT是工业应用最广泛的模型,工业数据大部分都极度偏态、具有长尾,因此GBDT必须考虑 **离群值** 带来的影响.
数据中的离群值会极大程度地影响模型地构建,当离群值在标签当中、而我们是依赖于减小损失函数来逐渐构建算法时,这种影响会前所未有地大.
举例来说,若离群值的标签为1000,大部分正常样本的标签在0.1~0.2之间,算法一定会异常努力地学习离群值的规律.
因为将离群值预测错误会带来巨大的损失. 在这种状况下,最终迭代出的算法可能是严重偏离大部分数据的规律的.
同样,我们也会遇见很多离群值对我们很关键的业务场景:
例如,电商中的金额离群用户可能是VIP用户,风控中信用分离群的用户可能是高风险用户,这种状况下我们反而更关注将离群值预测正确.
不同的损失函数可以帮助我们解决不同的问题.
- 当高度关注离群值、并且希望努力将离群值预测正确时,选择平方误差
这在工业中是大部分的情况.在实际进行预测时,离群值往往比较难以预测,因此离群样本的预测值和真实值之间的差异一般会较大.
MSE作为预测值和真实值差值的平方,会放大离群值的影响,会让算法更加向学习离群值的方向进化,这可以帮助算法更好地预测离群值.
- 努力排除离群值的影响、更关注非离群值的时候,选择绝对误差
MAE对一切样本都一视同仁,对所有的差异都只求绝对值,因此会保留样本差异最原始的状态.
相比其MSE,MAE对离群值完全不敏感,这可以有效地降低GBDT在离群值上的注意力!
- 试图平衡离群值与非离群值、没有偏好时,选择Huber或者Quantileloss.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 超参数优化
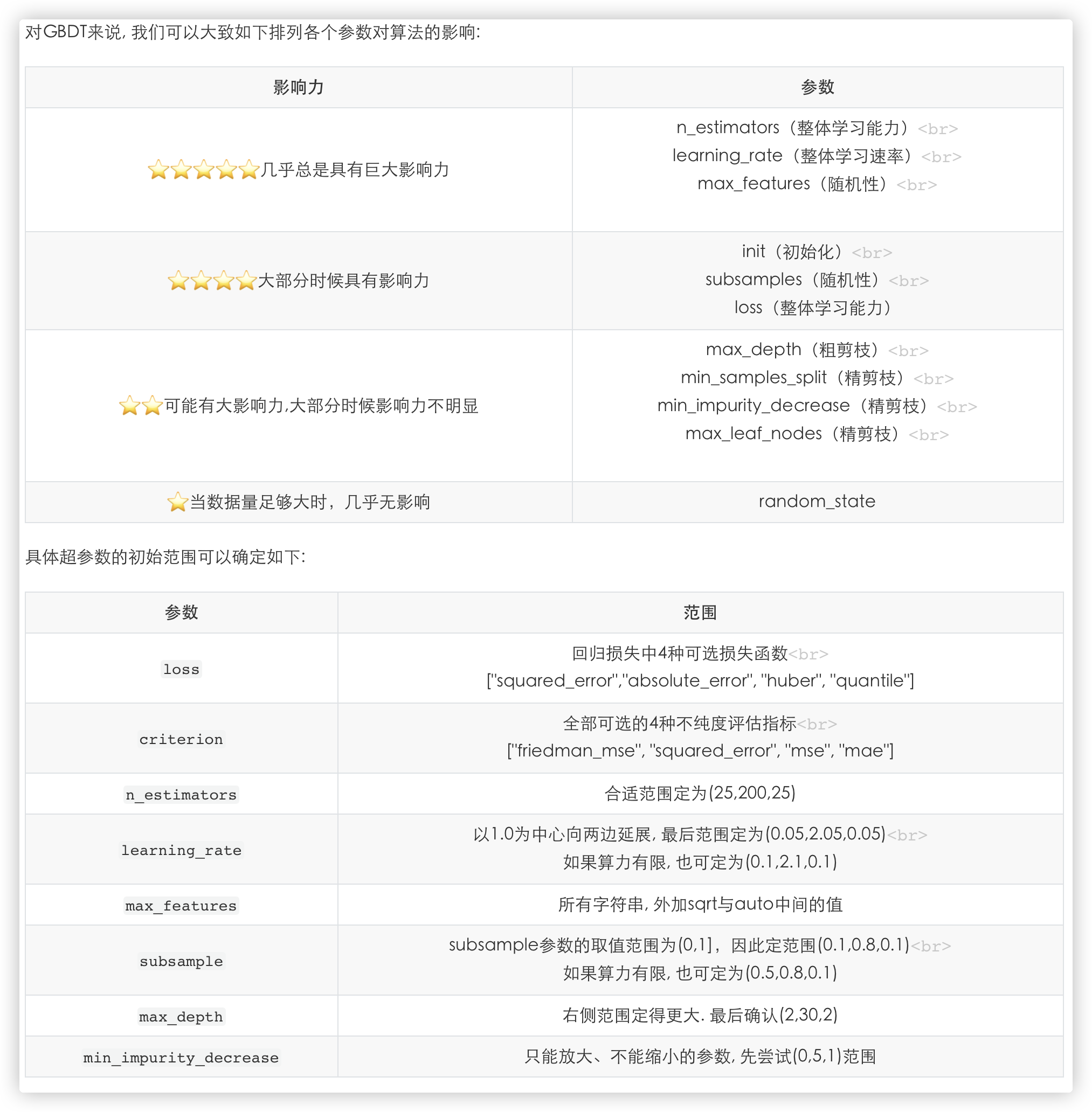
丰富的超参数为集成算法提供了无限的可能, 以降低偏差为目的的Boosting算法们在调参之后的表现更是所向披靡.
因此GBDT的超参数自动优化也是一个重要的课题.
对任意集成算法进行超参数优化之前, 我们需要明确一个基本事实: 不同参数对算法结果的影响力大小.
使用网格搜索去找.
# 回归测试
因此,GBDT的效果是要接近或者好于调完参的随机森林和Adaboost的结果!!
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.ensemble import GradientBoostingRegressor as GBR # GBDT回归
from sklearn.ensemble import AdaBoostRegressor as ABR # Adaboost
from sklearn.ensemble import RandomForestRegressor as RFR # 回归随机森林
from sklearn.model_selection import cross_validate, KFold # 交叉验证,折数规则制定
data = pd.read_csv(r"./House Price/train_encode.csv",index_col=0)
data.head(2)
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
def RMSE(result,name): #对每一折返回的根均方误差均值后取绝对值(以正数显示)
return abs(result[name].mean())
import time
modelname = ["GBDT回归","回归随机森林","Adaboost","调参后的回归随机森林","调参后的Adaboost"]
models = [GBR(random_state=8858), # GBDT回归
RFR(random_state=8858,n_jobs=-1), # 回归随机森林
ABR(random_state=8858), # Adaboost
RFR(n_estimators=89, max_depth=22,
max_features=14, min_impurity_decrease=0,
random_state=1412, verbose=False, n_jobs=-1), # 调参后的回归随机森林
ABR(n_estimators=39, learning_rate=0.94,
loss="exponential"
,random_state=8858) # 调参后的Adaboost
]
run_time = []
train_best_score = []
test_best_score = []
cv = KFold(n_splits=5,shuffle=True,random_state=8858)
for name,model in zip(modelname,models):
start = time.time()
result = cross_validate(model,X,y,cv=cv,
scoring="neg_root_mean_squared_error" # 负根均方误差(MSE开平方)
,return_train_score=True # 每一折的训练得分
,verbose=False
,n_jobs=-1) # n_jobs=-1使用所有可用的 CPU 核心来加速计算
end = time.time()-start
run_time.append(end)
train_best_score.append(RMSE(result,"train_score"))
test_best_score.append(RMSE(result,"test_score"))
# print(name)
# print("\t train_score:{:.3f}".format(RMSE(result,"train_score")))
# print("\t test_score:{:.3f}".format(RMSE(result,"test_score")))
# print("\t time:{:.2f}s".format(end))
# print("\n")
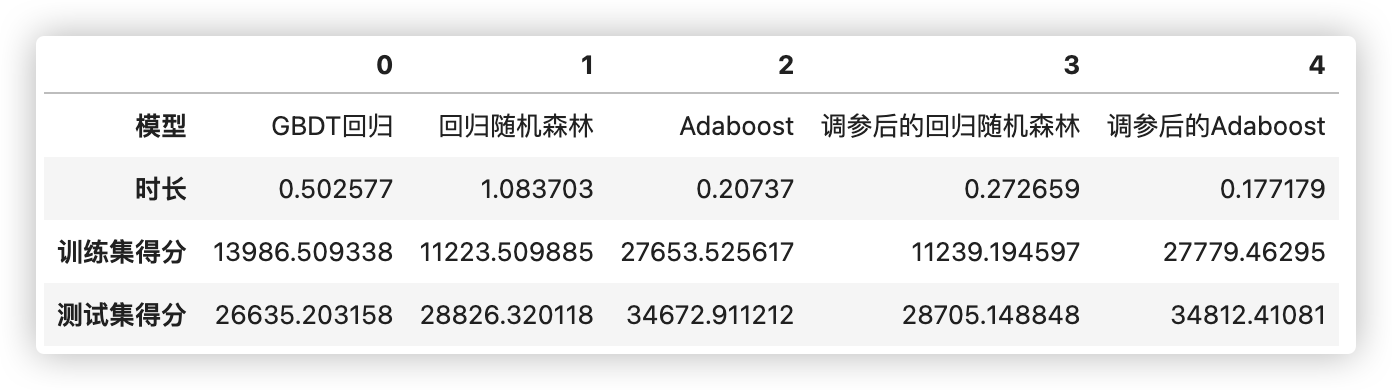
"""
当不进行调参时,随机森林的运行时间最长、AdaBoost最快,GBDT居中
但考虑到AdaBoost的`n_estimators`参数的默认值为50,而GBDT和随机森林的`n_estimators`默认值都为100,可以认为AdaBoost的运行速度与GBDT相差不多.
从测试集的得分结果来看,未调参状态下GBDT的结果是最好的,其结果甚至与经过精密调参后的随机森林结果相差不多.
而AdaBoost经过调参后没有太多改变.可以说AdaBoost极其缺乏调参空间、并且学习能力严重不足!
★ 因此,GBDT的效果是要接近或者好于调完参的随机森林和Adaboost的结果!
"""
pd.DataFrame([modelname,run_time,train_best_score,test_best_score],index=['模型','时长','训练集得分','测试集得分'])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# 分类测试
此处就不在和其他分类模型进行对比, 想要对比可以换成真正分类的数据集进行测试.
根据测试结果可知, GBDT还是要比xgboost和随机森林的分类效果要好!!
from sklearn.ensemble import GradientBoostingClassifier as GBC # GBDT分类
data = pd.read_csv(r"./House Price/train_encode.csv",index_col=0)
X_clf = data.iloc[:,:-2]
y_clf = data.iloc[:,-2]
clf = GBC(random_state=8858) # GBDT分类的实现
cv = KFold(n_splits=5,shuffle=True,random_state=8858)
result_clf = cross_validate(clf,X_clf,y_clf,cv=cv
,return_train_score=True
,verbose=True
,n_jobs=-1)
result_clf["train_score"].mean() # 训练集表现 0.9928082191780823
result_clf["test_score"].mean() # 测试集表现 0.8917808219178083
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
