统计学

这个世界充满了很多的不确定性, 我们希望通过统计学让这个不确定性更多的掌握在我们自己的手里.
通过某种有意义的方式对数据进行收集、处理、分析和解释, 使得仅仅通过观察原始数据无法立即水落石出的一些结论得以昭示.

关于统计学的公式, 我们只需要掌握和明白公式的组成部分表示的含义即可. 无需深究, 听个响就行, 哈哈哈.

统计学又分为了描述统计和推断统计两个重要的分支! .

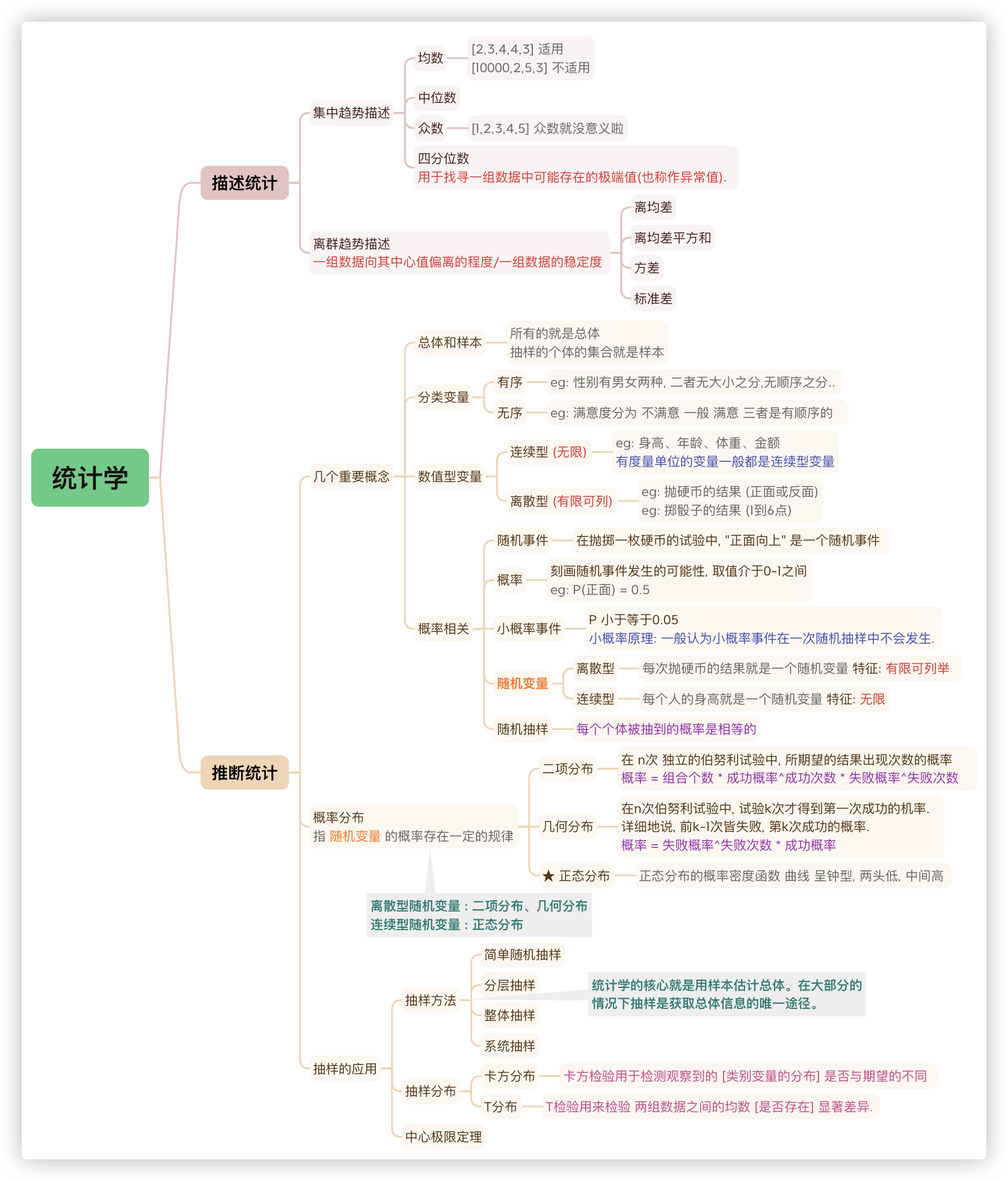
# 描述统计

啥叫描述统计,管它的呢.会用就行. 怎么用,从两个方面来用.
描述统计常用的两个维度(方面) - [集中趋势描述] 和 [离群趋势描述] 接下来且听我娓娓道来.

# 集中趋势描述

反映一组数据向其 [中⼼值] 靠拢或聚集的程度, 该程度通常使用均值、中位数和众数等指标来表示.

# 均数

一组数据中所有数据之和再除以这组数据的个数

⽐较敏感,数据任何⼀个值发⽣变化,均数都会随之改变!
[它将各个观测数据之间的差异性掩盖了] 此话怎讲? 一家公司平均薪资13k,看似美好,实则老板一人工资就是4w,占大头,其余的人3k-5k.

1
2

所以说,均值的适用范围对称分布的数据比较适用; 但极端性数据均数绝对不适⽤!

# 中位数

全体数据 "按顺序" 排列, 数据个数为奇数取中间位置那个数; 数据个数为偶数取中间位置两个数的平均值.

不受极端值的影响,在具有个别极⼤或极⼩值的分布数列中,中位数⽐均数更具有代表性.
中位数只考虑居中位置,其他变量值⽐中位数⼤多少或⼩多少,它⽆法反映出来,所以我们也是只能看到部分信息!

1
2

# 众数

⼀组数据当中, 出现次数最多的那个数

优点: 能够很好的反映数据的集中趋势 + 不易受数据中极端数值的影响
缺点: 当数据没有明显的集中趋势时,众数则完全无意义 eg: 1 2 3 4 5这种众数就没有意义啦.
  
举例说明众数的应用:
Q:如何决策一个造鞋厂对不同尺码的生产任务呢？
A:在大批量生产的男式皮鞋中有多种尺码,其中40码的销售量最多,这说明40码就是众数.
  可代表男式皮鞋尺码的一般水平,宜大量生产,而其余尺码的生产量就要相应少一些,这样才能满足市场上大部分消费者的需要.

1
2
3
4
5
6
7

# 四分位数

四分位数用于找寻一组数据中可能存在的极端值(也称作异常值).

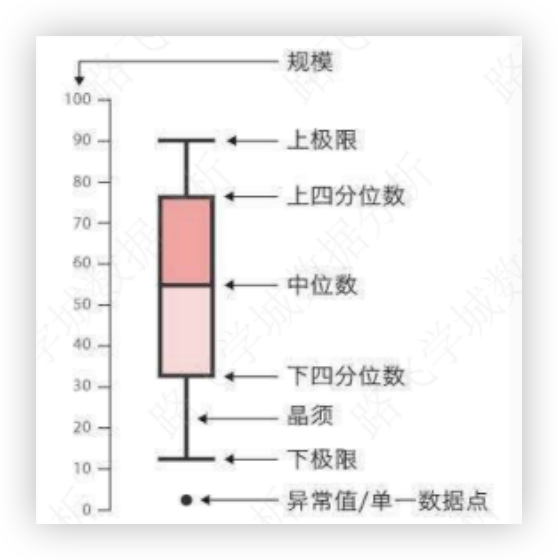
我们将一组数据 "按照顺序" 排列,并进行以下设定:

设定	含义
Q1	25%中位数, 也称为下四分位数
Q2	中位数
Q3	75%中位数, 也称为上四分位数
IQR	四分位距 = Q3 - Q1
MAX	上极限 = Q3 + `1.5` x `IQR`
MIN	下极限 = Q1- `1.5` x `IQR`

大于MAX(上极限) 和小于MIN(下极限) 的值, 我们将其叫做异常值!

# 离散趋势描述

反映一组数据向其中⼼值偏离的程度 / 一组数据的稳定度, 该程度通常使用方差或标准差等指标来表示.

eg: A组学生样本的标准差是17.06, B组学生样本的标准差是12.16 。那么证明A组学生之间的差距要比B组学生之间的差距大.

# 方差-标准差

指标	含义	公式
离均差	每一项与均值相差多远/离散程度	`x-μ`
离均差平方和	每一项的离均差相加不能体现整个样本的离散程度,因为有正有负,可抵消. 为了消除正负号的影响, 所以需要每一项的离均差需先平方,再相加	`∑(x-μ)²`
方差	当两个样本的数量相同, 离均差平方和越小的样本越稳定/离散程度越小那么两个样本的数量不相同呢? 就没有可比性了. 为了消除样本数量的影响,需要用到方差.即离均差平方和除以样本数量.	`∑(x-μ)² / n`
标准差	⽅差开根号就是标准差

让ChatGPT给我们举个例子:

# 推断统计

推断统计学是研究如何根据样本数据去推断总体数据的方法.

# 几个重要概念

# 总体和样本

术语	含义
总体	某批⽣产的所有灯泡就是总体
样本	在⼀个较⼤范围的研究对象中随机抽出⼀部分个体进⾏观察或预测, 这些个体的测量值构成的集合称为样本 eg: 随机从中抽取5%的灯泡进⾏检验, 随机抽取的5%的灯泡就是样本

# 分类变量

术语	含义	举例
无序分类变量	说明事物类别的⼀个名称	比如: 性别有男女两种, 二者无大小之分,无顺序之分.. 同理, 血型、民族也是.
有序分类变量	说明事物类型的⼀个名称, 但是有次序之分	例如: 满意度分为不满意一般满意三者是有顺序的

So, 非数值的数据都要进行分类, 注意有序和无序之分. 因为建模时,对其所作的预处理的手段是不一样的!

# 数值型变量

术语	含义	举例
连续型变量	它可以在一个或多个连续的区间内任意取值, 可以是无限多个可能的值	身高、年龄、体重、金额
离散型变量	它的取值通常是可数的、整数的, 且有限或者有限可列	抛硬币的结果 (正面或反面) 掷骰子的结果 (1到6点)

经验而言, 有度量单位的变量一般都是连续型变量.

# 概率相关

术语	含义
随机事件	eg: 在抛掷一枚硬币的试验中, "正面向上" 是一个随机事件
概率	刻画随机事件发生的可能性, 取值介于0-1之间 eg: P(正面) = 0.5
小概率事件	-1- 如果随机事件发⽣的概率⼩于或等于0.05, 则它是⼀个⼩概率事件, 表示该事件在⼤多数情况下不会发⽣ -2- ⼩概率原理: ⼀般认为⼩概率事件在⼀次随机抽样中不会发生. ⼩概率原理是推断统计的基础.
随机变量	抛硬币, 只有正面和反面的两种结果. -- 抛硬币正反面这个随机变量就是离散型的身高, 有无数种结果. -- 身高这个随机变量就是连续型的.
随机抽样	每个个体最终是否⼊选在抽样进⾏前是不可知的但是其⼊选的可能性是确切可知的（每个个体被抽到的概率是相等的）

随机变量可分为离散型随机变量和连续性随机变量.

随机变量 >> 随机事件的数量化.
⽐如：抛硬币,出现正⾯，我们定义为"成功",记为1 ; 出现反⾯定义为"失败", 记为0. 
     那{0 ,1} 就是本次实验的结果的量化值,为随机变量可能出现的值.

随机变量又可分为离散型随机变量和连续性随机变量.
  - 离散型随机变量
    - 随机变量X可以⼀⼀列举出来,在⼀定区间范围内X是有限个的,可数的. 
      例如: 抛硬币 X可取1或0
  - 连续性随机变量
    - 随机变量X⽆法⼀⼀列举出来,在⼀定区间范围内是⽆限个的,不可数的. 
      例如: 统计北京市30岁以上男性身⾼, 每个⼈的身⾼都不⼀样, 测量单位⼀定的情况下, 数据是连续的.

1
2
3
4
5
6
7
8
9
10
11

# 概率分布

随机变量的概率存在⼀定的规律, 这个规律叫做概率分布

离散型随机变量的概率分布有: 二项分布、几何分布 - 这两个与伯努利试验有关;
连续型随机变量的概率分布有: 正态分布

★何为伯努利试验? 指单次随机试验, 只有"成功" 和 "失败" 这两种结果.

# 二项分布

⼆项分布是指在 n次独⽴的伯努利试验中, 所期望的结果出现次数的概率

二项分布的公式如下:

ps: 3! = 3*2*1

关于二项分布的系数 C(n,k) 举个例子就很好理解了.

抛5次硬币,2次正面朝上的情况有种? 有10种情况（出现正面记为T,反面记为F）-- 就是排列组合
TTFFF,FTTFF,FFTTF,FFFTT,TFTFF,FTFTF,FFTFT,TFFTF,FTFFT,TFFFT -- 可能出现在第一次第二次;第一次第三次;等

1
2

公式中各个变量的含义如下:

变量	含义
X	随机变量X
n	指进行伯努利试验的总次数
k	指在n次伯努利试验中成功发生/出现期望的结果的次数为k次
p	指每次伯努利试验成功的概率/出现期望结果的概率
1-p	指每次伯努利试验失败的概率
C(n,k)	指组合数, 表示从n次试验中选择k次成功的方式数

案例1: 某篮球队的一名运动员进行定点投篮, 假设每次投中的概率是0.6, 求他投10次中8次的概率.
计算过程: {10! / [8! * (10-8)!]} * 0.6^8 * (1-0.6)^(10-8)

案例2:
盒子中装有8个彩球(红球4个+绿球2个+黄球2个), 现在有放回的取3次, 每次取一个小球, 求取到的3个小球恰好有两个红球的概率.

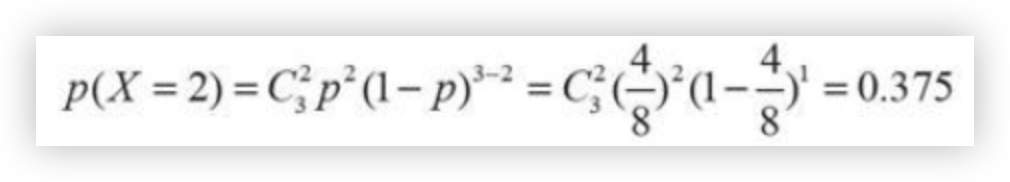
# 几何分布

在n次伯努利试验中, 试验k次才得到第一次成功的机率. 详细地说, 前k-1次皆失败, 第k次成功的概率.

几何分布的公式如下:

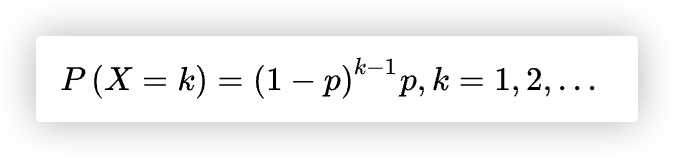
案例: 抛硬币, 正面反面的概率都是1/2, 求抛到第三回才第一次出现正面的概率.
计算过程: (1-0.5)^(3-1) * 0.5

# 正态分布

正态分布曲线呈钟型, 两头低, 中间高

正态分布的概率密度函数如下:

该概率密度函数的曲线长这个样子:

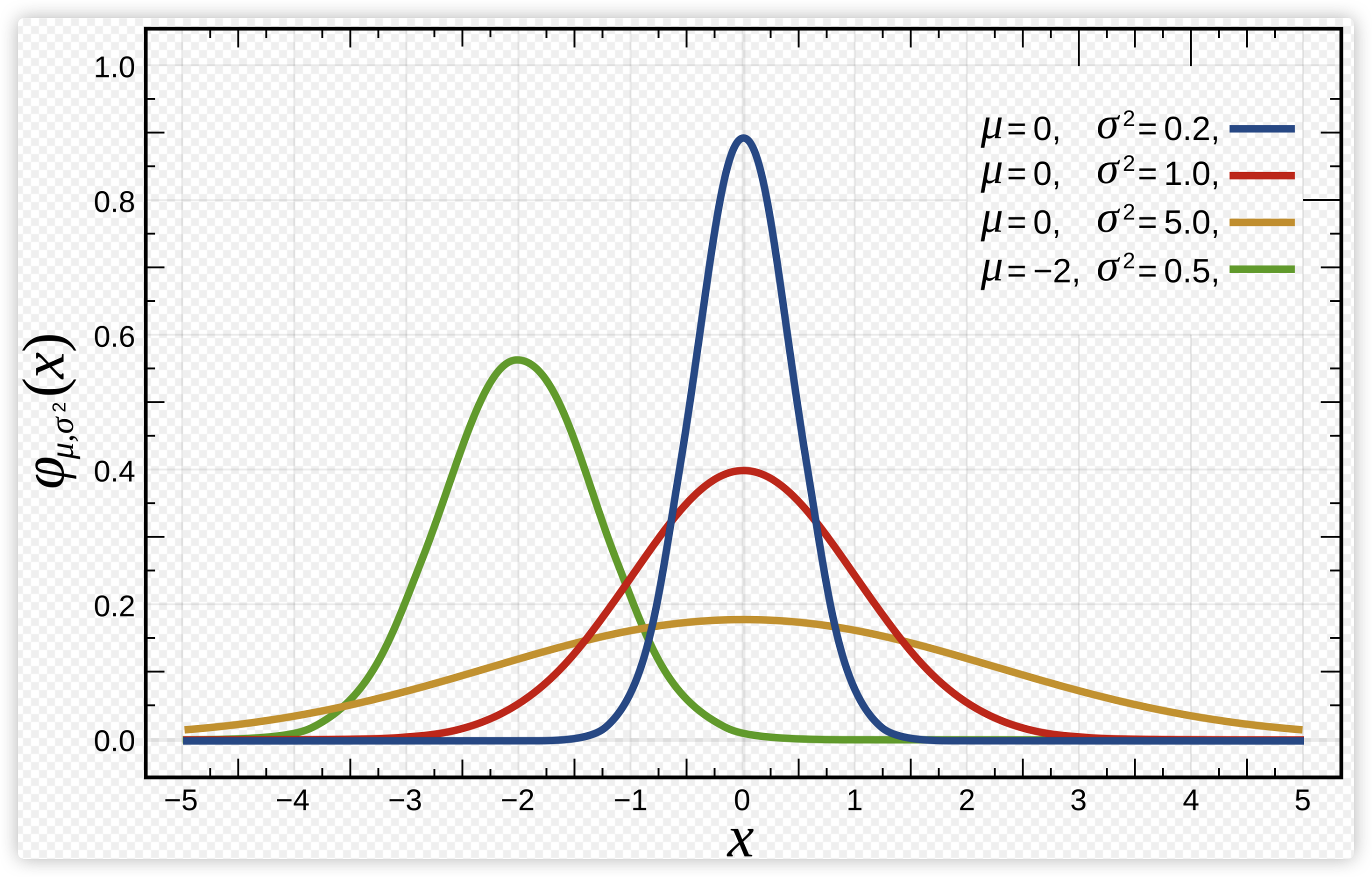
在后续的数据分析和机器学习中会经常看到它的身影.Hhh.
正态曲线的背景知识点: 95%的数据分布在均值周围2个标准差的范围内 ; μ=0, 𝛔^2=1 则叫做标准正态分布.

参数μ 表示均值 ; 参数𝛔 表示标准差 / 𝛔^2则是方差
人的身高是符合正态分布的,求一个人身高为170的概率. 将x=170代入函数即可!

1
2

# 抽样的应用

数据量小时很容易收集, 但数据量大时, 就很难决定该如何有效的、正确的和省时省力的收集数据了.
这时, 就需要用到统计学的 [样本抽样] 了

说在前面:
抽样分布是啥? 所有的样本/每组样本的统计量(均值、方差等) 形成的分布就是样本的抽样分布.
借助总体分布来理解, 全国人民的身高分布符合正态分布, 呈现钟型, 两头低, 中间高. 那么每组样本的均值呈现的曲线就是抽样分布.

抽样分布呈现的曲线有三种, 卡方分布、T分布、F分布. 在这里我们了解下前两个.
卡方分布、T分布定义、公式啥的很青涩难以理解. 非专业人士, 琢磨不透. 我们知道它的作用即可!

# 抽样方法

统计学的核心就是用样本估计总体. 在大部分的情况下抽样是获取总体信息的唯一途径.
因此为了实现这一目的, 我们可以采取简单随机抽样、分层抽样、整体抽样和系统抽样这些方式进行抽样.

简单随机抽样: 从包括总体N个抽样单位的总体中随机地、一个一个地抽取n个单位作为样本.
系统抽样: 将总体中的所有抽样单位按照一定顺序进行排列, 然后每隔k个单位进行一次抽样,其中k为一个特定的数字.

整群抽样与分层抽样的区别:
-1- 分层抽样要求各层之间的差异很大,层内个体或单元差异小; 而整群抽样要求群与群之间的差异比较小,群内个体或单元差异大;
-2- 分层抽样的样本是从每个层内抽取若干单元或个体构成; 而整群抽样则是要么整群抽取,要么整群不被抽取.

>> 举个栗子: 口香糖有 香蕉、苹果、梨子 三种口味.
分层 - 香蕉口味的所有口香糖为一层;苹果口味的所有口香糖为一层;梨子口味的所有口香糖为一层
整群 - 每一盒口香糖都有n片香蕉味的、n片苹果味的、n片梨子味的. 每一盒口香糖形成一个群!

1
2
3
4
5
6
7
8
9
10

# 抽样分布之卡方分布

卡方分布的作用: 卡方检验
卡方检验用于检测观察到的 [类别变量的分布] 是否与期望的不同

首先举两个栗子来了解卡方分布的自由度.

① 假设我们有5个年龄段, 我们想要检验这些年龄段的分布是否符合均匀分布的预期.
在这种情况下, 卡方分布的自由度将是 k−1 = 5−1 = 4, 其中 k 是年龄段的数量.

② 掷骰子, 我们想验证每个点的分布是否符合均匀分布的预期.
在这种情况下, 卡方分布的自由度将是 k−1 = 6−1 = 5, 其中 k 是骰子的面数.

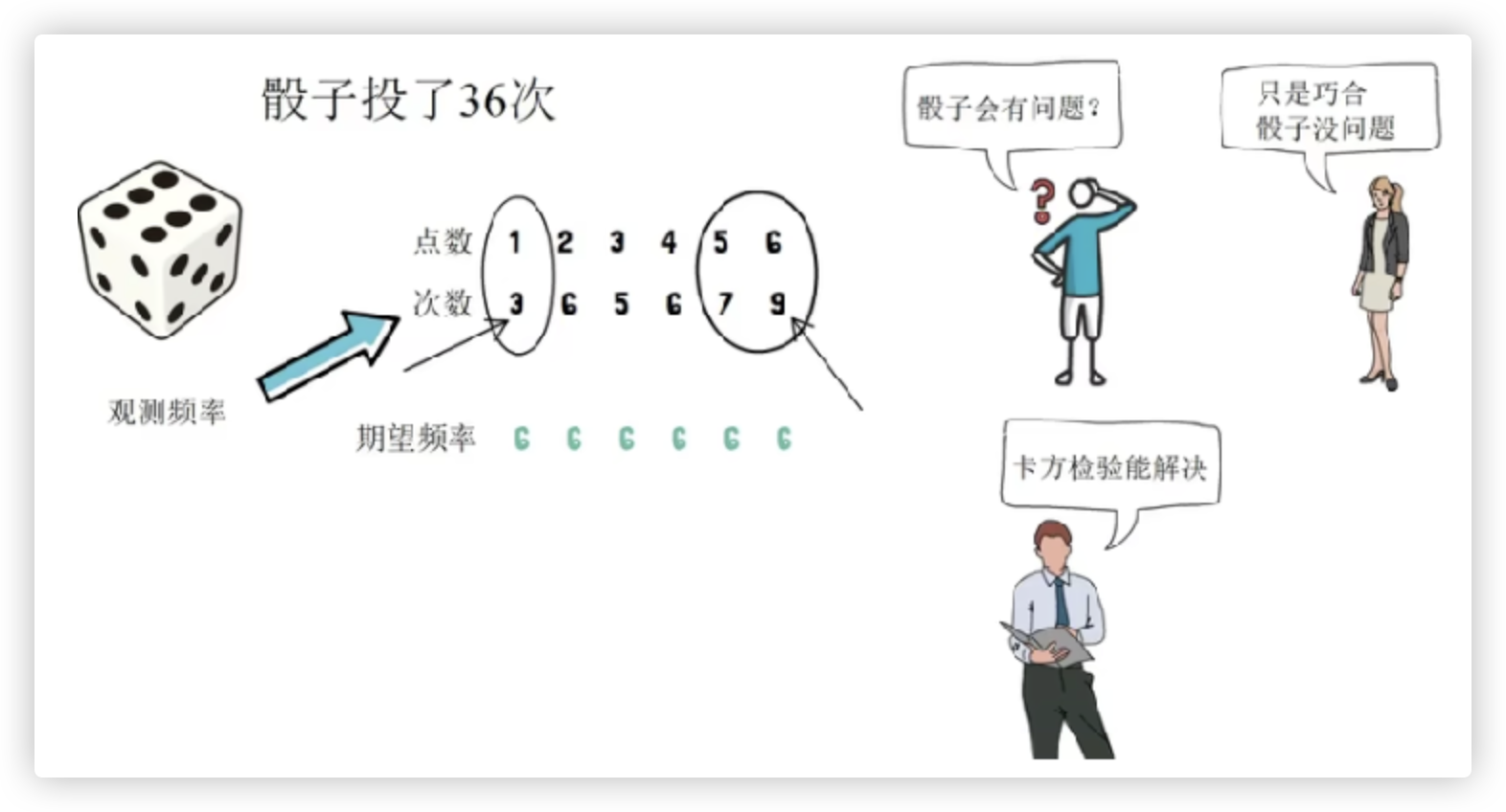
进行了36次投骰子实验, [每次投掷都可看作是一个样本, 每个样本的统计量是投掷的结果].
这个投掷的结果/每个样本的统计量的分布按照我们的预期应该是均匀分布的. 也就是 1点-6点, 都会出现6次. 函数上体现是一条直线.

但真实的样本统计量分布曲线呈现的样子不是我们想的那样的, 点数高的面次数多, 点数少的面次数少.
所以, 我们就说骰子有问题?? 为了证明实验结果的有效性, 就要进行卡方拟合度检验.

卡方拟合度检验的步骤如下:
-step1- 计算每个面的理论频数（假设均匀分布下每面出现的次数期望相同）.
-step2- 计算卡方统计量.
-step3- 使用卡方分布的分位点或p值来判断观察到的频数是否与理论分布一致.

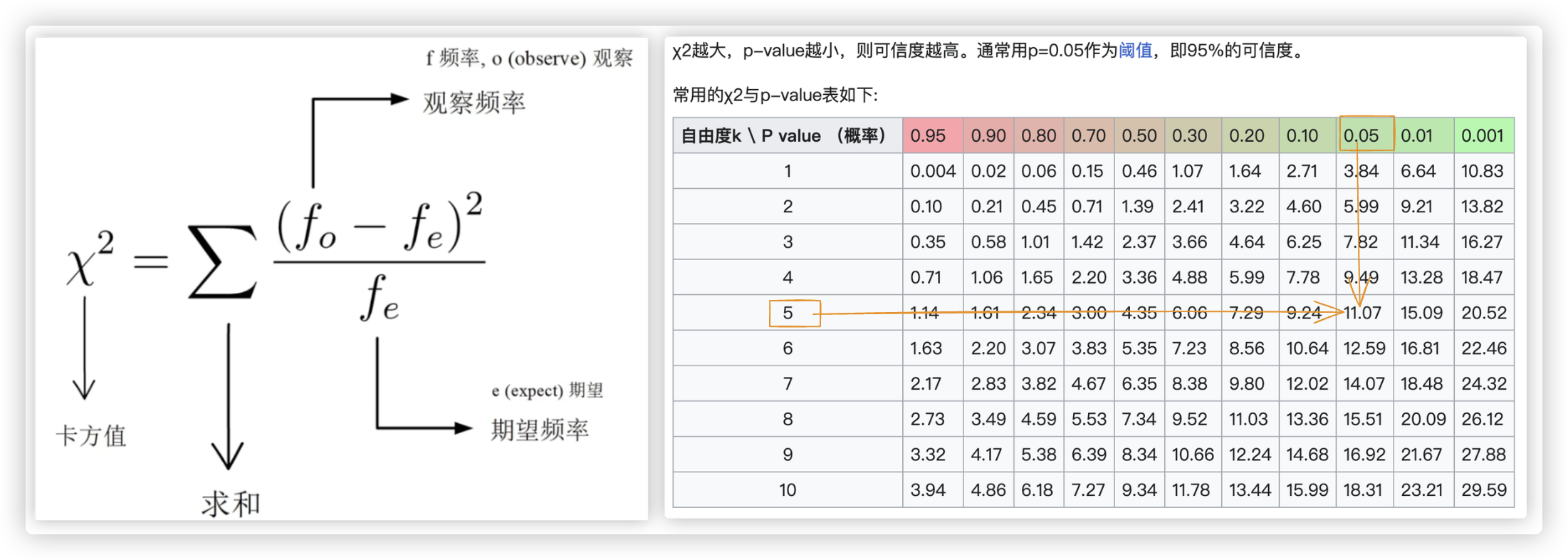
在此示例卡中
f = (3-6)^2/6 + (6-6)^2/6 + (5-6)^2/6 + (6-6)^2/6 + (7-6)^2/6 + (9-6)^2/6
  =  3/2 + 0 + 1/6 + 0 + 1/6 + 3/2
  =  10/3 ≈ 3.3333
  
统计量可能的值,也就是1点-2点-3点-4点-5点-6点,共6种 (也可以理解成类别)
统计量的情况数减去1就是自由度k

3.3333 < 11.07 所以该次实验是有效的!

1
2
3
4
5
6
7
8
9

# 抽样分布之T分布

T分布的作用: T检验
T检验用来检验两组数据之间的均数是否存在显著差异.

案例: A班体育成绩的平均分是 80分, B班体育成绩的平均分是82分. 那么如何确定一个班是强于另一个班的呢?

单纯比较平均分是不准确的,用T检验来证明!

我们可以发现:
1.组间差异越大,t值越大
2.组内差异越大,t值越小
3.样本量越大,t值越大

■ 使用T检验的满足条件:
1.被测量的变量（两个班级的分数）需要在总体和样本中呈现正态分布。
  注:根据t分布可知,当自由度/样本量大于30则t分布近似正态分布
2.两个样本之间的方差不能相差太多。