KNN算法

额, 关于代码编写你直接看 knn回归任务代码实现 这一小节的代码 + 超参数 这一小节的代码..
大体步骤:
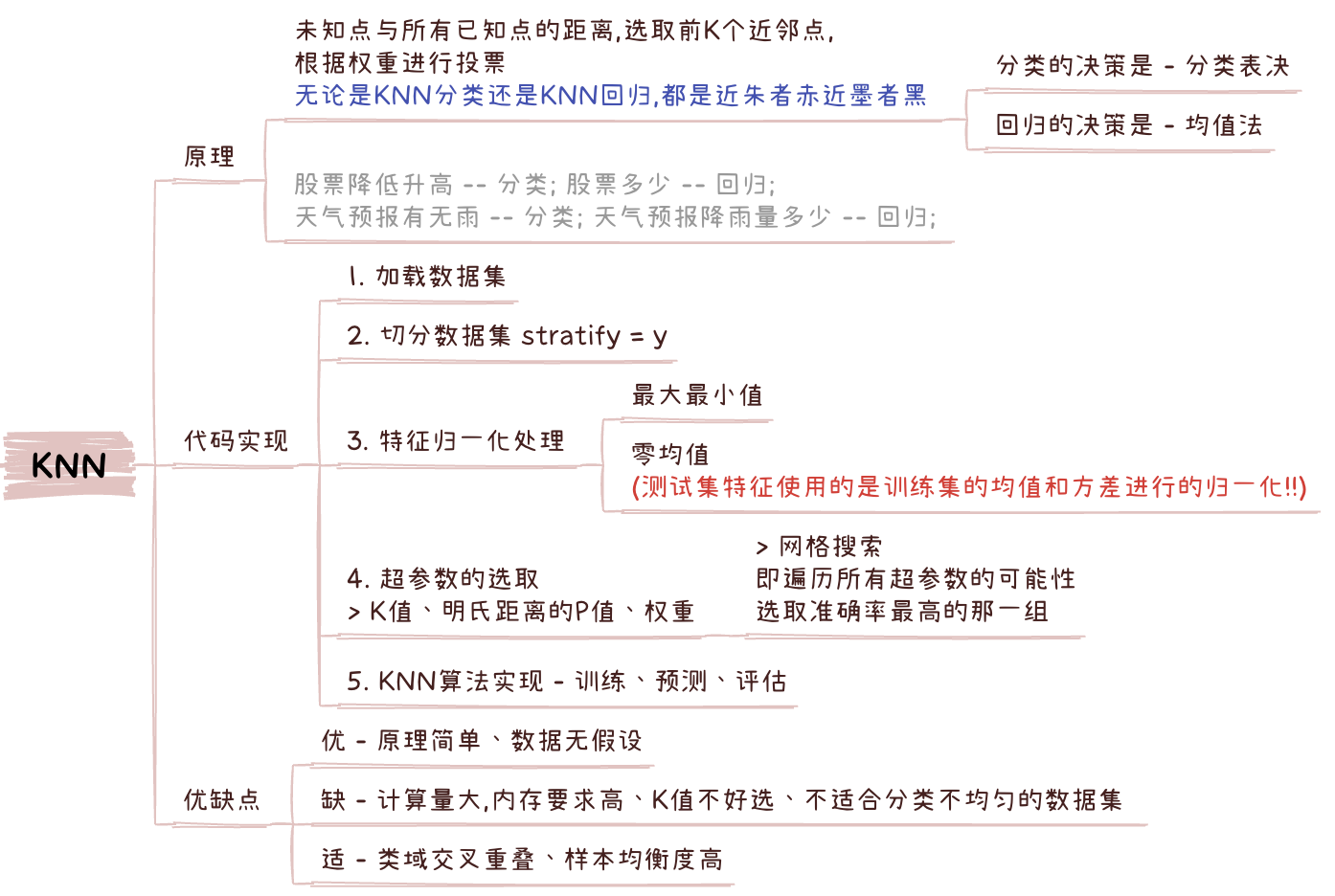
- 加载数据集 - 划分数据集 - 特征归一化(训练集特征、测试集特征) - 超参数的选取 - KNN算法

# 思想和原理

# KNN分类任务代码实现

"""
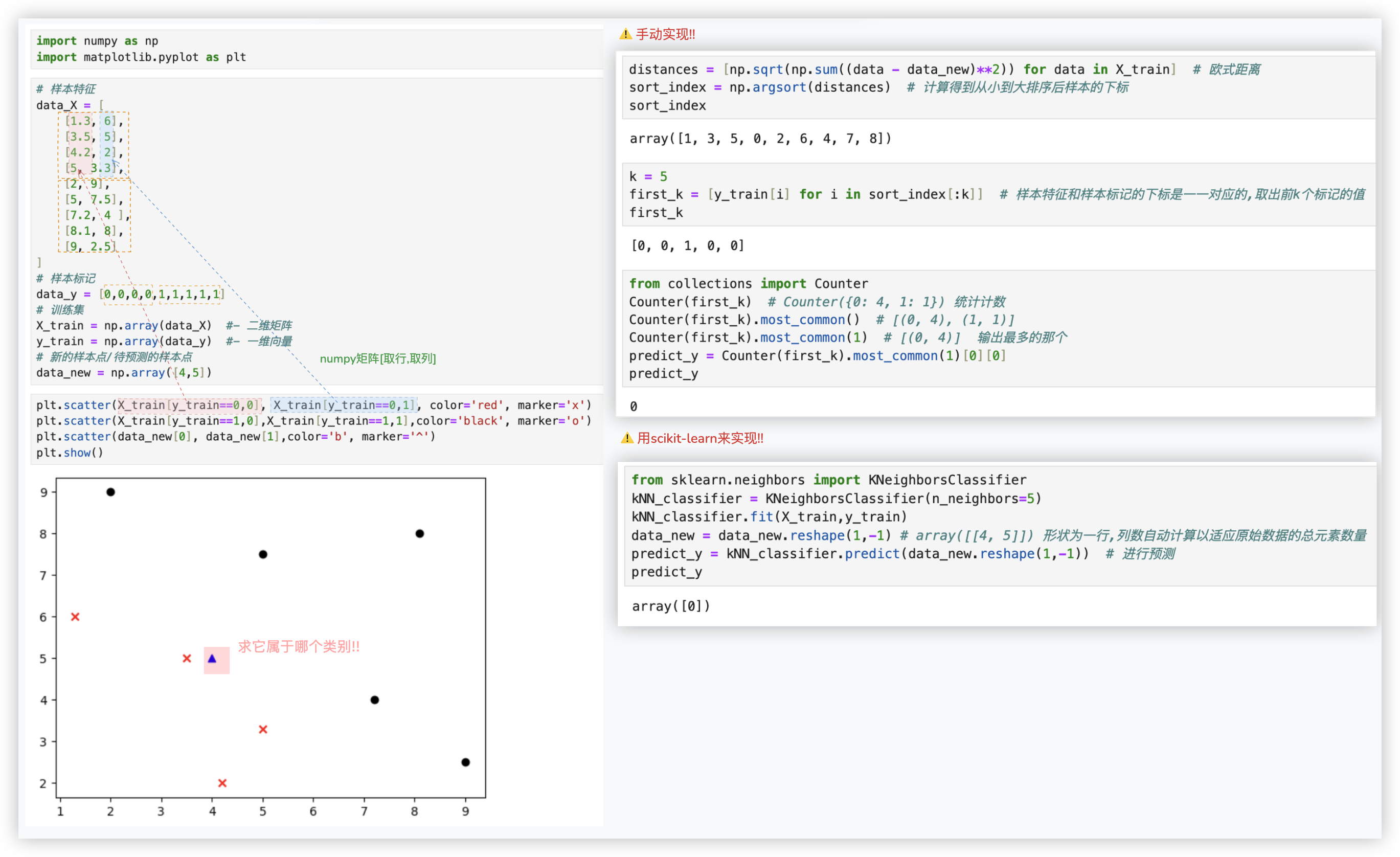
准备数据,并画图看数据的分布
"""
import numpy as np
import matplotlib.pyplot as plt

# 样本特征
data_X = [
    [1.3, 6],
    [3.5, 5],
    [4.2, 2],
    [5, 3.3],
    [2, 9],
    [5, 7.5],
    [7.2, 4 ],
    [8.1, 8],
    [9, 2.5]
]
# 样本标记
data_y = [0,0,0,0,1,1,1,1,1]
# 训练集
X_train = np.array(data_X)  #- 二维矩阵
y_train = np.array(data_y)  #- 一维向量
# 新的样本点/待预测的样本点
data_new = np.array([4,5])

plt.scatter(X_train[y_train==0,0], X_train[y_train==0,1], color='red', marker='x')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='black', marker='o')
plt.scatter(data_new[0], data_new[1],color='b', marker='^')
plt.show()


"""
手动实现KNN算法对未知点进行预测
"""
distances = [np.sqrt(np.sum((data - data_new)**2)) for data in X_train]  # 欧式距离
sort_index = np.argsort(distances)  # 计算得到从小到大排序后样本的下标
sort_index

k = 5
first_k = [y_train[i] for i in sort_index[:k]]  # 样本特征和样本标记的下标是一一对应的,取出前k个标记的值
first_k

from collections import Counter
Counter(first_k)  # Counter({0: 4, 1: 1}) 统计计数
Counter(first_k).most_common()  # [(0, 4), (1, 1)]
Counter(first_k).most_common(1)  # [(0, 4)]  输出最多的那个
predict_y = Counter(first_k).most_common(1)[0][0]
predict_y


"""
使用sklearn封装好的KNN算法对未知点进行预测
"""
from sklearn.neighbors import KNeighborsClassifier
kNN_classifier = KNeighborsClassifier(n_neighbors=5)
kNN_classifier.fit(X_train,y_train)
data_new = data_new.reshape(1,-1) # array([[4, 5]]) 形状为一行,列数自动计算以适应原始数据的总元素数量
predict_y = kNN_classifier.predict(data_new.reshape(1,-1))  # 进行预测
predict_y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

# 数据集拆分

"""
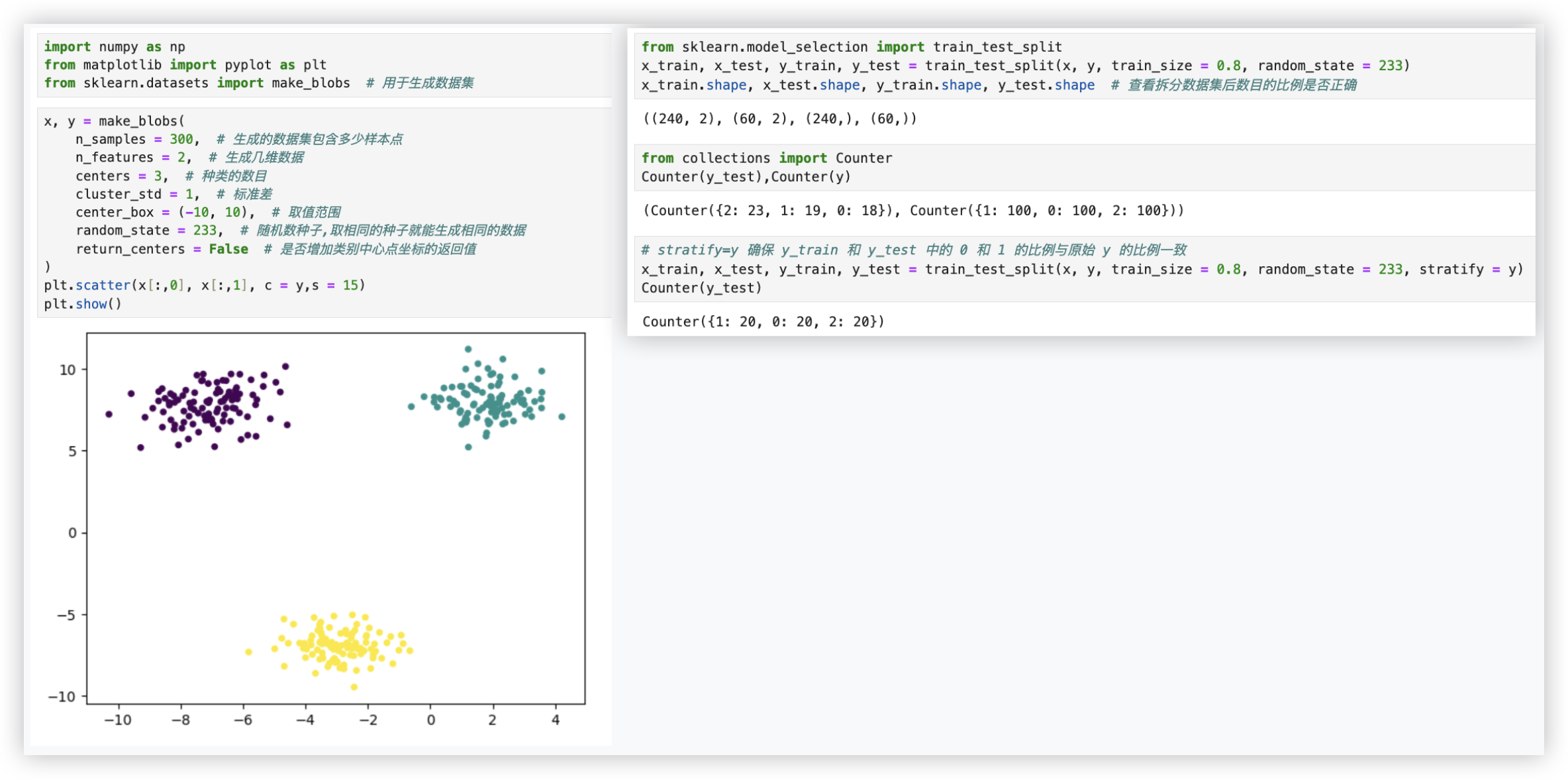
准备数据,并展示数据的分布
"""
import numpy as np 
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobs  # 用于生成数据集

x, y = make_blobs(
    n_samples = 300,  # 生成的数据集包含多少样本点 
    n_features = 2,   # 生成几维数据
    centers = 3,      # 种类的数目
    cluster_std = 1,  # 标准差
    center_box = (-10, 10),  # 取值范围
    random_state = 233,      # 随机数种子,取相同的种子就能生成相同的数据
    return_centers = False   # 是否增加类别中心点坐标的返回值
)
plt.scatter(x[:,0], x[:,1], c = y,s = 15)
plt.show()


"""
将数据集二八分
"""
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.8, random_state = 233)
x_train.shape, x_test.shape, y_train.shape, y_test.shape  # 查看拆分数据集后数目的比例是否正确

from collections import Counter
Counter(y_test),Counter(y)  # 发现类别数据的比例跟原y中类别的比例不一致

# stratify=y 确保 y_train 和 y_test 中的 0 和 1 的比例与原始 y 的比例一致
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.8, random_state = 233, stratify = y)
Counter(y_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 模型评价

加载数据集 - 划分 - 训练、预测 - 评估

"""
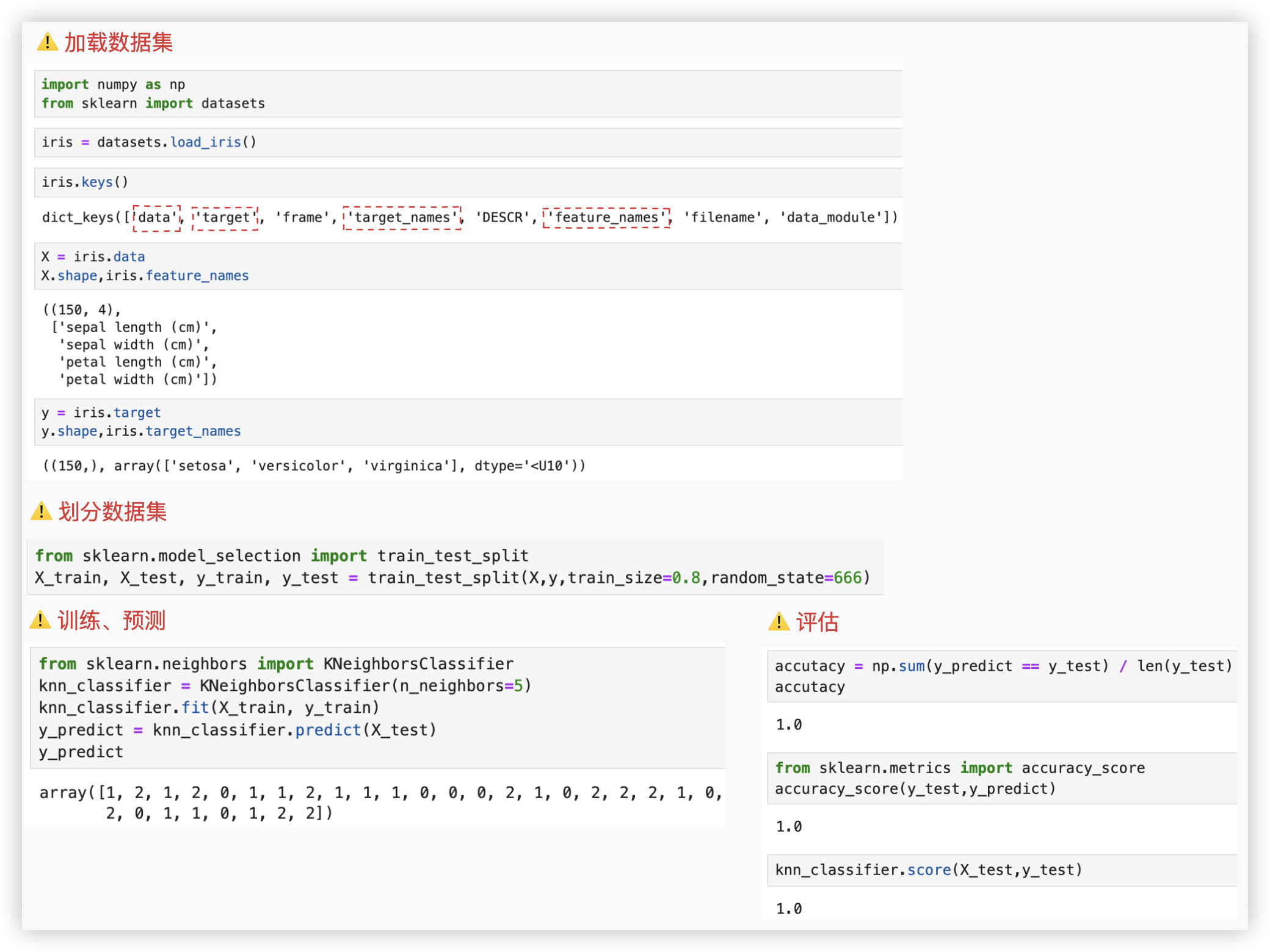
加载数据集
"""
import numpy as np
from sklearn import datasets

iris = datasets.load_iris()
iris.keys()

X = iris.data
X.shape,iris.feature_names

y = iris.target
y.shape,iris.target_names

"""
划分数据集
"""
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,train_size=0.8,random_state=666)

"""
训练、预测
"""
from sklearn.neighbors import KNeighborsClassifier
knn_classifier = KNeighborsClassifier(n_neighbors=5)
knn_classifier.fit(X_train, y_train)
y_predict = knn_classifier.predict(X_test)
y_predict

"""
评估
"""
accutacy = np.sum(y_predict == y_test) / len(y_test)
accutacy

from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)

knn_classifier.score(X_test,y_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 超参数Hyperparameter

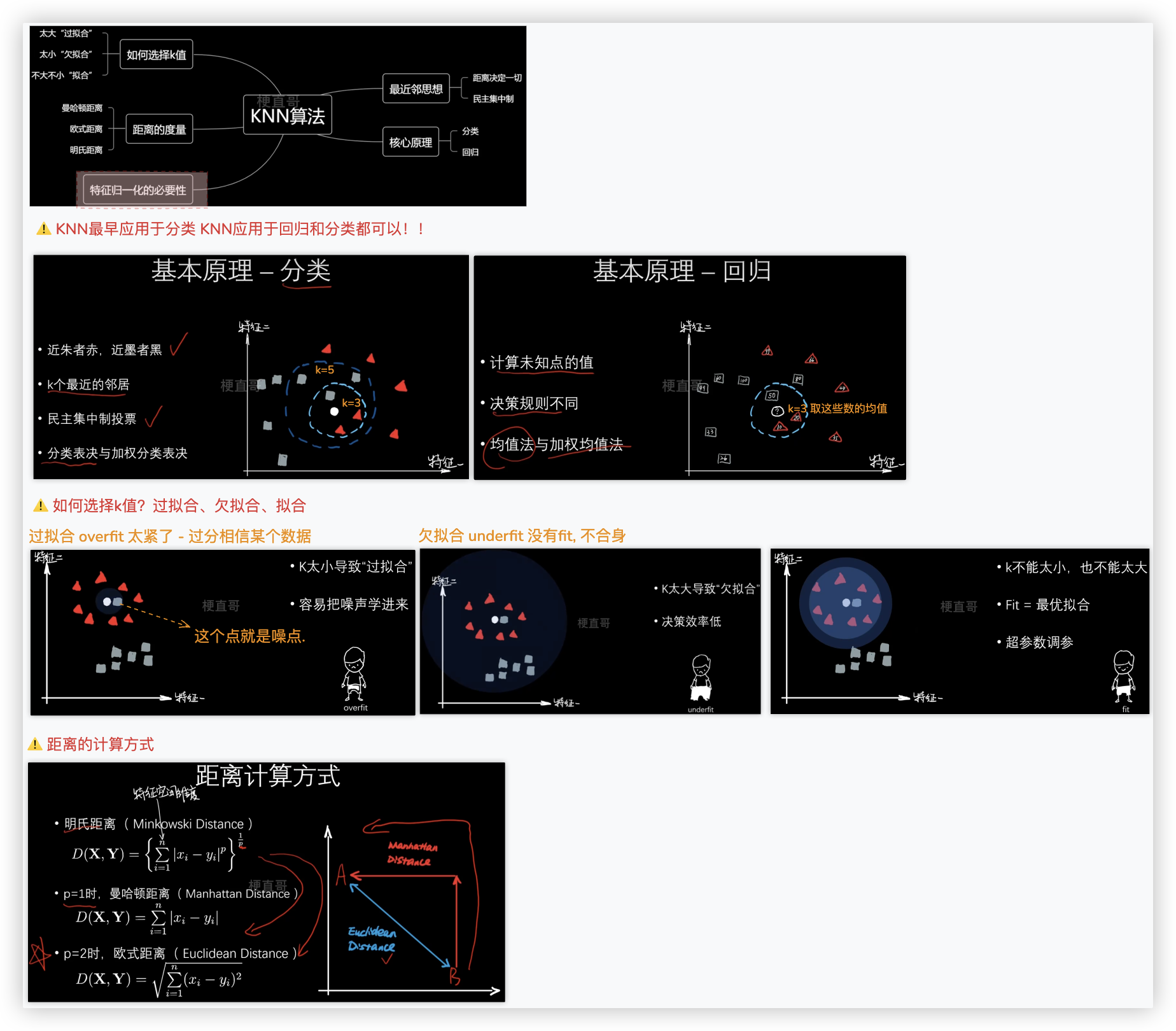
需要人为设置的参数, 就叫作超参数, 比如: k值.. 如何设置,通常可从两方面进行参考:
- 根据经验
- 让机器根据准确率自行搜索 eg: 网格搜索 - 遍历所有超参数的可能性, 选取准确率最高的那一组..
KNN算法的超参数
- K值
- 近邻点的权重 (分类表决和权重表决)
- 明氏距离的p值 (p=1,p=2)

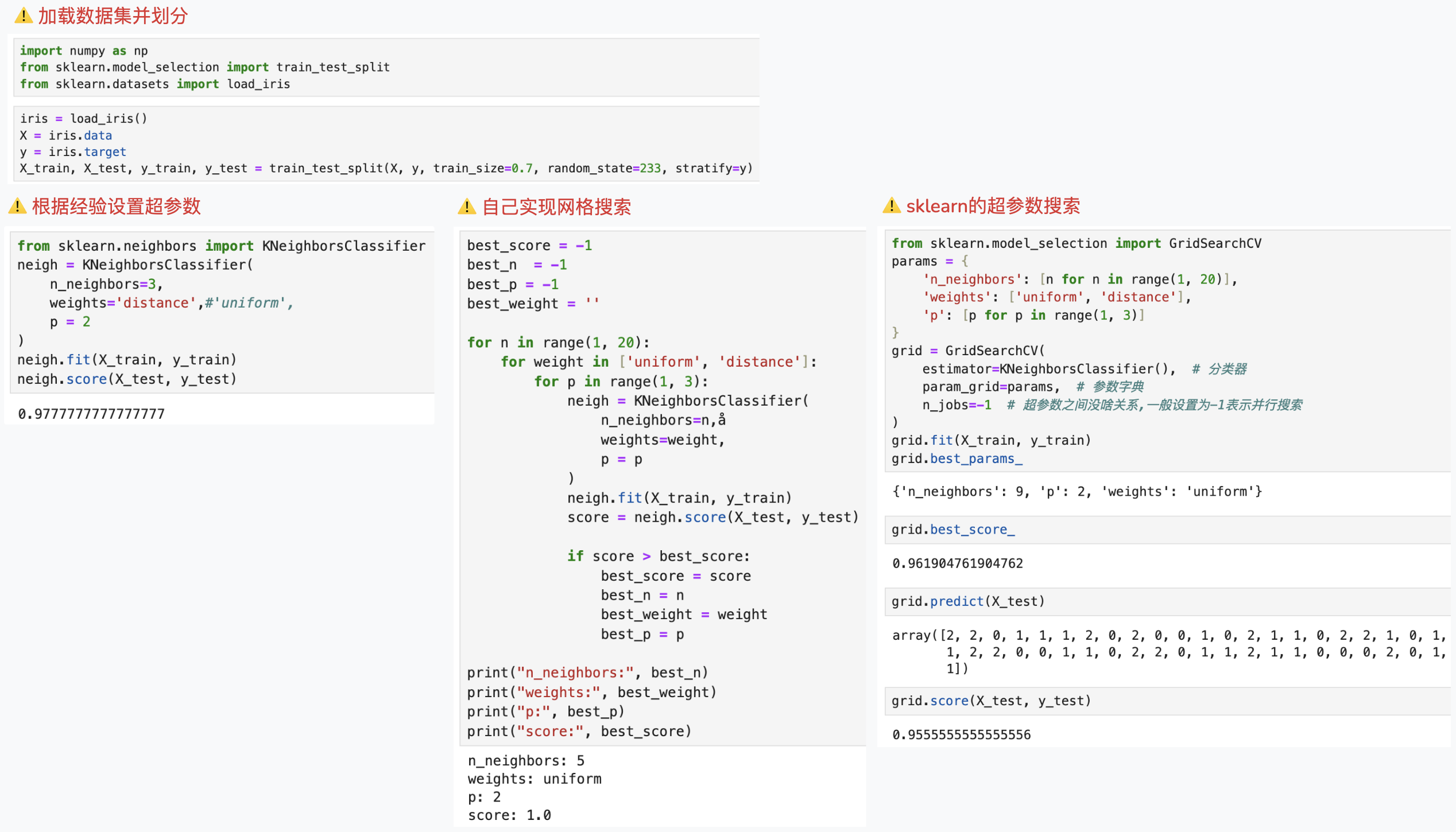
PS: 细心的你可能会观察到, 基于sklearn和自行实现超参数搜索得到结果的不一样, 是准确率方法计算不同导致的..暂且不纠结..

"""
加载数据集并划分
"""
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=233, stratify=y)


"""
根据经验设置超参数
"""
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(
    n_neighbors=3,
    weights='distance',#'uniform',  distance表示越近权重越高
    p = 2
)
neigh.fit(X_train, y_train)
neigh.score(X_test, y_test)


"""
自己实现网格搜索
"""
best_score = -1
best_n  = -1
best_p = -1
best_weight = ''

for n in range(1, 20):
    for weight in ['uniform', 'distance']:
        for p in range(1, 3):
            neigh = KNeighborsClassifier(
                n_neighbors=n,å
                weights=weight,
                p = p
            )
            neigh.fit(X_train, y_train)
            score = neigh.score(X_test, y_test)
            
            if score > best_score:
                best_score = score
                best_n = n
                best_weight = weight
                best_p = p

print("n_neighbors:", best_n)
print("weights:", best_weight)
print("p:", best_p)
print("score:", best_score)


"""
sklearn的超参数搜索
"""
from sklearn.model_selection import GridSearchCV
params = {
    'n_neighbors': [n for n in range(1, 20)],
    'weights': ['uniform', 'distance'],
    'p': [p for p in range(1, 3)]
}
grid = GridSearchCV(
    estimator=KNeighborsClassifier(),  # 分类器
    param_grid=params,  # 参数字典
    n_jobs=-1  # 超参数之间没啥关系,一般设置为-1表示并行搜索
)
grid.fit(X_train, y_train)
grid.best_params_

grid.best_score_

grid.predict(X_test)

grid.score(X_test, y_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

# 特征归一化

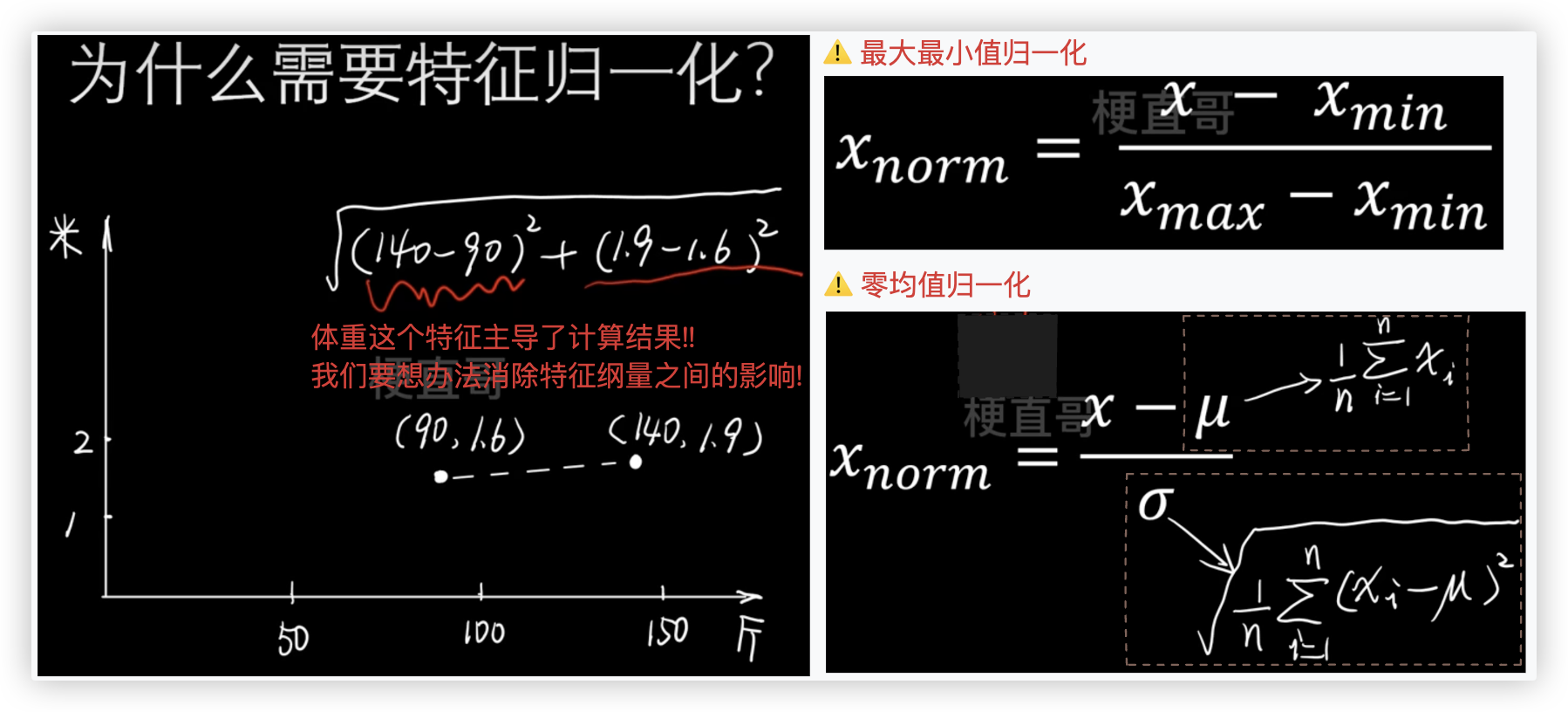
代码实现, 以零均值归一化为例, 通常也是使用它!

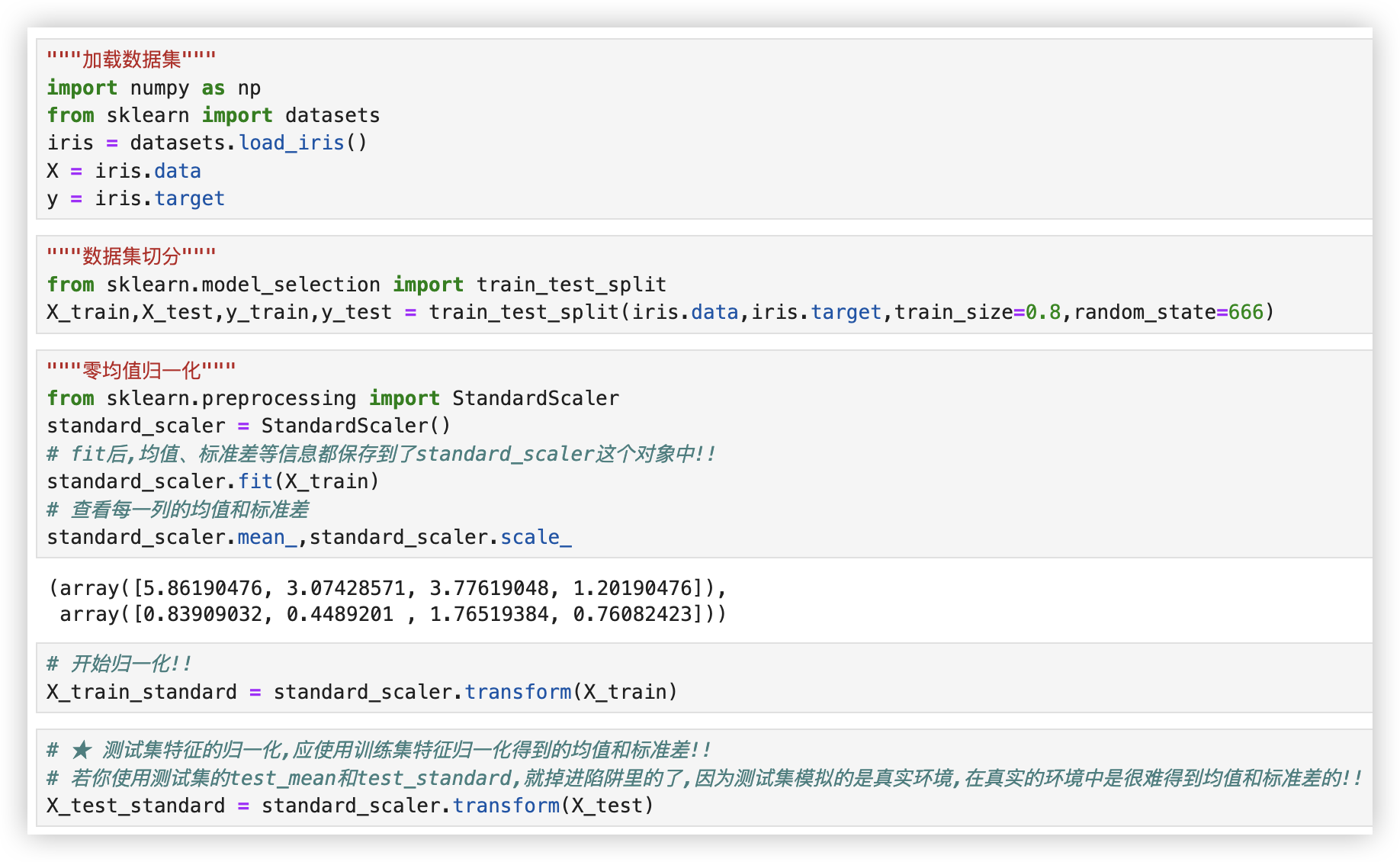
★ 特别强调 - 测试集特征的归一化,应使用训练集特征归一化得到的均值和标准差

"""加载数据集"""
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

"""数据集切分"""
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,train_size=0.8,random_state=666)

"""零均值归一化"""
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
# fit后,均值、标准差等信息都保存到了standard_scaler这个对象中!!
standard_scaler.fit(X_train)  
# 查看每一列的均值和标准差
standard_scaler.mean_,standard_scaler.scale_

# 训练集特征开始归一化!!
X_train_standard = standard_scaler.transform(X_train)

# ★★★★ 测试集特征的归一化,应使用训练集特征归一化得到的均值和标准差!!
# - 若你重新对测试集特征归一化,使用测试集特征的test_mean和test_standard,就掉进陷阱里的了
#   因为测试集模拟的是真实环境,在该环境中是很难得到均值和标准差的!!  (PS 列数都一样.)
X_test_standard = standard_scaler.transform(X_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# KNN回归任务代码实现

股票降低升高 -- 分类; 股票多少 -- 回归;
天气预报有无雨 -- 分类; 天气预报降雨量多少 -- 回归;
knn即可作分类也可作回归, 两者都是近朱者赤近墨者黑,
但两者的决策规则不一样 knn分类是分类表决; knn回归是均值法..
当然 knn更适合作分类!!

自己创建训练集进行训练, 再创建一个未知点对其进行预测..

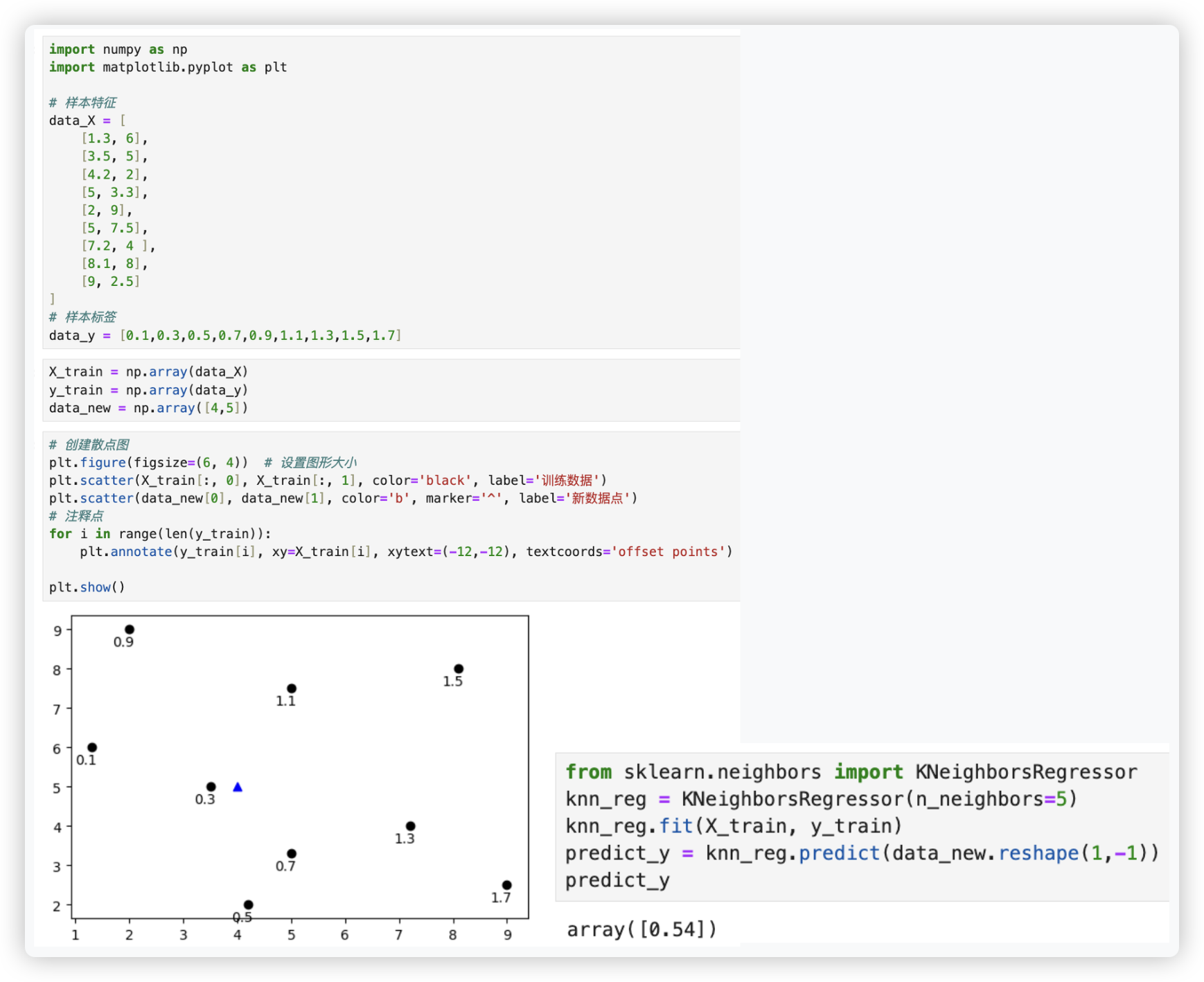
import numpy as np
import matplotlib.pyplot as plt

# 样本特征
data_X = [
    [1.3, 6],
    [3.5, 5],
    [4.2, 2],
    [5, 3.3],
    [2, 9],
    [5, 7.5],
    [7.2, 4 ],
    [8.1, 8],
    [9, 2.5]
]
# 样本标签
data_y = [0.1,0.3,0.5,0.7,0.9,1.1,1.3,1.5,1.7]

X_train = np.array(data_X)
y_train = np.array(data_y)
data_new = np.array([4,5])

# 创建散点图
plt.figure(figsize=(6, 4))  # 设置图形大小
plt.scatter(X_train[:, 0], X_train[:, 1], color='black', label='训练数据')
plt.scatter(data_new[0], data_new[1], color='b', marker='^', label='新数据点')
# 注释点
for i in range(len(y_train)):
    plt.annotate(y_train[i], xy=X_train[i], xytext=(-12,-12), textcoords='offset points')

plt.show()

from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor(n_neighbors=5)
knn_reg.fit(X_train, y_train)
predict_y = knn_reg.predict(data_new.reshape(1,-1))
predict_y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

再来看看,KNN回归模型在公开数据集上的表现.. (暂且不用关注效果, 先聚焦代码的实现..

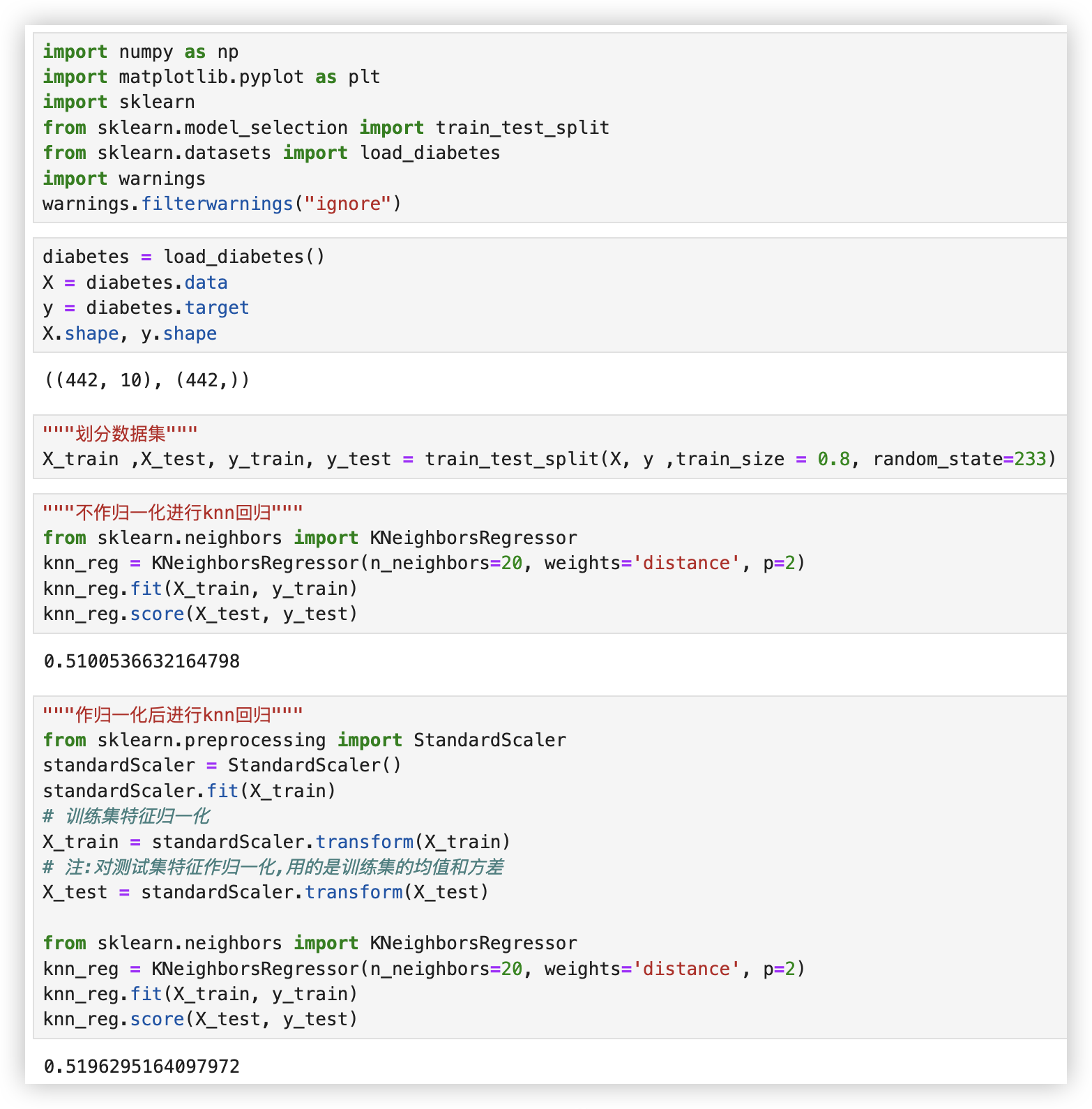
import numpy as np
import matplotlib.pyplot as plt
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
import warnings
warnings.filterwarnings("ignore")

diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X.shape, y.shape

"""划分数据集"""
X_train ,X_test, y_train, y_test = train_test_split(X, y ,train_size = 0.8, random_state=233)

"""不作归一化进行knn回归"""
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor(n_neighbors=20, weights='distance', p=2)
knn_reg.fit(X_train, y_train)
knn_reg.score(X_test, y_test)

"""作归一化后进行knn回归"""
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
# 训练集特征归一化
X_train = standardScaler.transform(X_train)
# 注:对测试集特征作归一化,用的是训练集的均值和方差
X_test = standardScaler.transform(X_test)

from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor(n_neighbors=20, weights='distance', p=2)
knn_reg.fit(X_train, y_train)
knn_reg.score(X_test, y_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# KNN优缺点和适应条件

优点
- 思想简单、理论成熟、数据无假设/对数据不挑剔
缺点
- K值不好选
- 计算量大(涉及距离计算的算法都有这个弊端)、内存要求高
- 不适合样本类别不平衡的数据集
适用
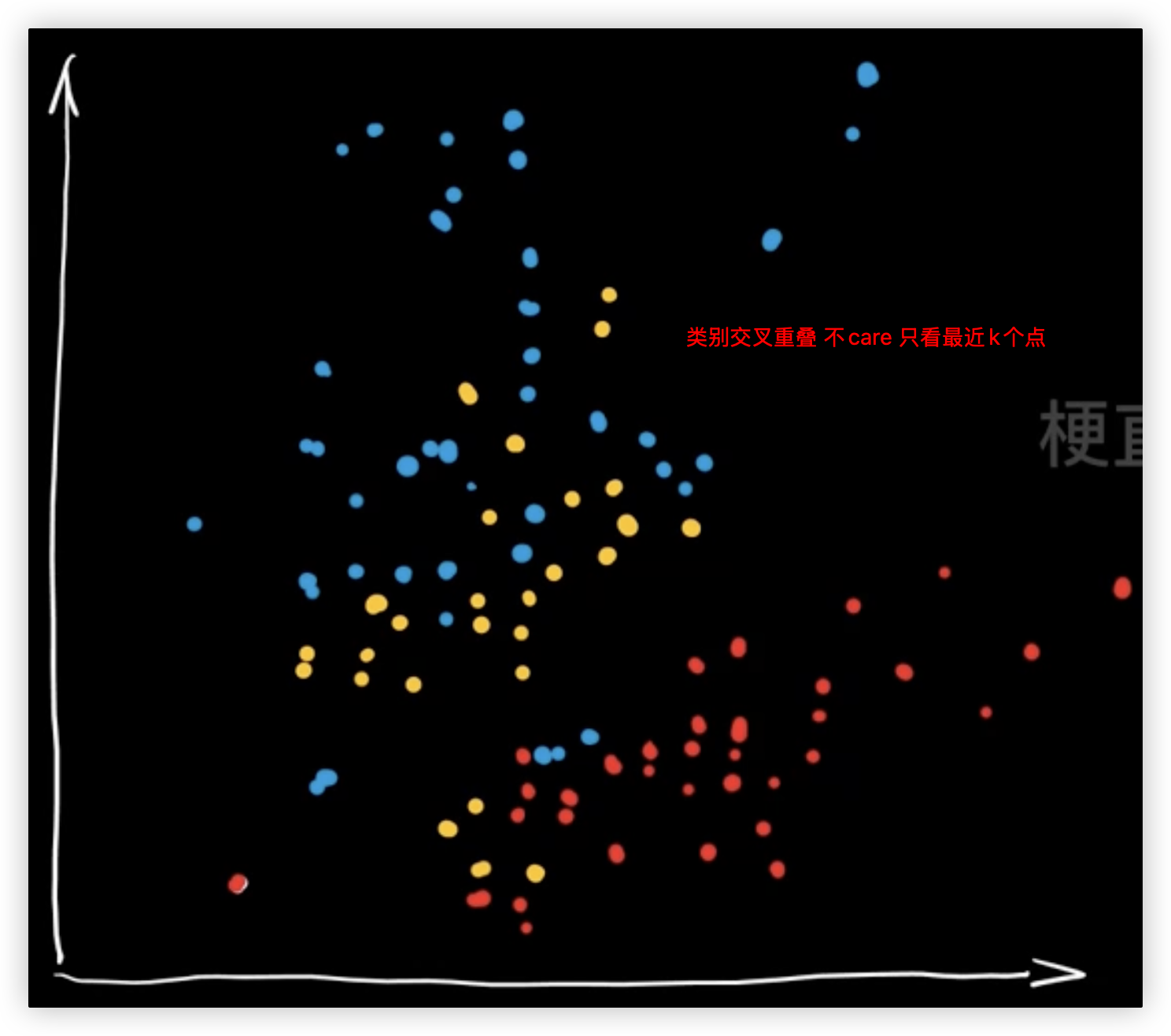
- 类域交叉重叠
- 样本均衡度高
可改进的方面 - 速度优化、样本优化、距离公式、K值的选取

← 开篇线性算法→