在上一篇博客中,简单二分类的示例,用到了交叉熵损失函数, 该篇博客,我们来进一步探究损失函数.

• 是什么?
  在PyTorch中, 损失函数（Loss Function）是用于衡量模型预测结果与真实值之间差异的函数.
• 有何作用?
  根据模型在训练过程中的损失,作反向传播,进而去优化不同网络层级中所对应的权重系数w.
• 根据任务的不同, 常用的损失函数可以分为分类问题和回归问题两大类.
  在传统机器学习中, 我们就说过, 分类和回归场景下, 损失函数的量化标准是不一样的.
  • 回归/预测 - 基于预测结果与真实结果之间的差异来表示损失.
  • 分类 - 基于模型分类出的结果的类别 与 真实类别之间进行对比, 一致则分类正确, 否则就分类错误.

注意: 关于损失函数, 记住有哪些损失函数即可, 公式的推导、公式的展示不重要..

---

分类场景

计算损失, 通常情况下:

损失函数	任务场景	备注
交叉熵、负对数交叉熵	多分类任务	前者计算损失时,会自动将模型的输出进行softmax后计算损失 模型输出若不是概率分布, 后者需要手动对模型输出进行softmax后才能开始计算损失
二元交叉熵	二分类任务	前提 二分类+输出层设置了sigmoid作为激活函数

也就是说,你看别人写好的模型输出层已经用了softmax,那你直接用负对数交叉熵作为损失函数.. emm

交叉熵损失

对数似然损失/交叉熵损失 - 在分类任务中最常用 - 在传统机器学习的"逻辑回归"中我们遇到过它!

CrossEntropyLoss（交叉熵损失）是深度学习和机器学习中常用的一种损失函数, 特别是在分类问题中.
它衡量的是模型预测的概率分布与真实标签的概率分布之间的差异.
它主要刻画的是实际输出（概率）与期望输出（概率）的距离, 也就是交叉熵的值越小, 两个概率分布就越接近.

• 特点与优势
  • 直观反映差异.
    能够直观地反映模型预测与真实标签之间的差异, 当预测概率分布越接近真实标签的概率分布时, 损失值越小
  • 优化效果显著.
    能够鼓励模型对正确的类别给出更高的预测概率, 同时对错误的类别给出更低的预测概率, 从而优化模型的分类性能
  • 适用于多分类问题.
    只要应用了交叉熵损失, 最后一层输出层无需使用激活函数..  
    直接接受模型的原始输出和标签, 内部自动应用softmax函数 获得/输出 样本分到每个类别的概率. 进而得到损失
    (关于这个的解释,详看 ''一点思考" 这一小节的内容.)
• 适用场景
• 二分类、多分类 eg: 图像分类、文本分类等

import torch
import torch.nn as nn
import torch.optim as optim

# - 生成一些示例数据 10行2列
X = torch.randn(10, 2)  # 10个样本,每个样本有2个特征维度
y = torch.tensor([0, 1, 2, 0, 1, 2, 0, 1, 2, 0])  # 对应的标签,有3个类别

# - 定义一个简单的神经网络模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        # 构建网络结构,只有一个输入层一个输出层 
        # 其中输入层两个神经元; 输出层3个神经元(即一个样本经过前向传播后会得到3个结果)
        self.fc = nn.Linear(2, 3)
    
    def forward(self, x):  
        return self.fc(x)

model = SimpleNN()

# model.state_dict() 获取的是模型经过训练后,迭代更新的那些w.. 
# 因为现目前还未更新,所以该表达式当前的结果跟list(model.parameters())中看到的随机初始w一样.
list(model.parameters())
"""
[Parameter containing:
 tensor([[ 0.5799, -0.1186],
         [ 0.1837,  0.6035],
         [-0.4165, -0.2333]], requires_grad=True),
 Parameter containing:
 tensor([-0.5565, -0.6662,  0.5126], requires_grad=True)]
"""

criterion = nn.CrossEntropyLoss()  # 定义交叉熵损失函数
outputs = model(X)  # 前向传播,该示例没有使用激活函数.
print(outputs)      # 得到的是模型第一次经过前向传播后,输出层输出,每个样本分到这三个类别的概率(简单理解成概率即可)
"""
tensor([[ 3.2686e-01, -8.4726e-01,  1.0721e-01],
        [-4.9192e-01,  2.8906e-01,  1.8591e-03],
        [-9.0283e-01, -1.0934e+00,  9.1913e-01],
        [-6.6142e-01, -4.6981e-01,  4.7393e-01],
        [-2.0044e+00, -6.3563e-01,  1.3095e+00],
        [ 2.7159e-01, -8.9600e-01,  1.6242e-01],
        [-1.0771e+00, -1.1754e+00,  1.0576e+00],
        [-1.1541e+00, -4.2125e-01,  7.2608e-01],
        [-4.3548e-01, -4.8878e-01,  3.5664e-01],
        [-3.0517e-01, -4.6784e-01,  2.7316e-01]], grad_fn=<AddmmBackward0>)
"""

loss = criterion(outputs, y)  # 计算损失
print("CrossEntropyLoss:", loss.item())
"""
CrossEntropyLoss: 1.2275140285491943
"""

负对数似然损失

NLLLoss, 全称为Negative Log Likelihood Loss（负对数似然损失）, 是一种在深度学习中常用的损失函数.
尤其在处理分类问题时表现突出. 工作原理与交叉熵损失函数非常相似.

NLLLoss衡量了模型预测概率分布与真实标签之间差异的损失.
具体来说, 它通过对模型输出的对数概率进行 [负化处理] 来评估预测的准确性.
在分类任务中, 如果模型的预测越接近真实标签, 则NLLLoss的值越小, 表示模型性能越好.
(负化处理的作用原理是啥,无需知道,肯定有它的道理的,用就行 公式的推导同理)

• 特点与优势

  • 负对数似然损失通常用于当模型输出已经是概率分布时的情况
  • 如果模型的原始输出不是概率分布时, 需要手动应用softmax等函数将输出转化为概率分布.

• 适用场景

  • 适用于当模型输出已经是概率分布时的情况

(･_･; 下面这个示例,模型的输出不是概率分布的,为了进行负对数似然损失的计算.
需要将model(x)前向传播的结果手动进行softmax转换成概率后,才能代入负对数似然损失函数中进行损失的计算..

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim


# - 生成一些示例数据
X = torch.randn(10, 2)
y = torch.tensor([0, 1, 2, 0, 1, 2, 0, 1, 2, 0])  # 对应的标签

# 定义一个简单的神经网络模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc = nn.Linear(2, 3)
    
    def forward(self, x):
        return self.fc(x)

model = SimpleNN()

# -定义负对数似然损失函数
criterion = nn.NLLLoss()

# -计算损失前需要手动应用softmax或log_softmax函数
#  模型的原始输出不是概率分布时,需要手动应用softmax等函数将输出转化为概率分布。
outputs = model(X)
# ★★★★★★
# 或者使用 softmax >> log_probs = F.log_softmax(F.softmax(outputs, dim=1), dim=1)
log_probs = F.log_softmax(outputs, dim=1)
loss = criterion(log_probs, y)
print("NLLLoss:", loss.item())

"""
NLLLoss: 1.1804684400558472
"""

二元交叉熵损失

二分类任务中, 输出层使用了sigmoid作为激活函数, 在这两前提下, 你就可以使用 二元交叉熵作为损失函数!!!

BCELoss, 全称为Binary Cross-Entropy Loss, 即二元交叉熵损失函数, 是深度学习中用于二分类问题的一种常用损失函数.
它用于衡量模型预测的概率分布与实际标签之间的差异, 从而指导模型的优化方向.

BCELoss广泛应用于二分类问题中, 如图像分类、文本分类等场景. 在这些场景中, 模型需要预测样本属于两个类别中的哪一个.
BCELoss通过衡量模型预测的概率分布与实际标签之间的差异, 帮助模型学习正确的分类决策.

注意: 在二分类问题中, 通常将BCELoss与Sigmoid激活函数结合使用, 以将模型的原始输出转换为概率值.

import torch
import torch.nn as nn
import torch.optim as optim

# - 生成一些示例数据
X = torch.randn(10, 1)  # 10个样本,每个样本有1个特征
# 对应的标签,注意是浮点型,并调整形状
y = torch.tensor([0, 1, 0, 1, 0, 1, 0, 1, 0, 1], dtype=torch.float32).view(-1, 1)

# - 使用 Sequential 定义一个简单的神经网络模型
model = nn.Sequential(
    nn.Linear(1, 1),
    nn.Sigmoid()  # 使用sigmoid激活函数将输出转换为[0, 1]范围内的概率值
)

# - 定义二元交叉熵损失函数
criterion = nn.BCELoss()

# - 计算损失
outputs = model(X)
loss = criterion(outputs, y)
print("BCELoss:", loss.item())

"""
BCELoss: 0.7655717730522156
"""

---

回归场景

经验之谈: 在回归场景中,计算损失,通常会先使用MSE,效果不好,再试试Huber..

MSE

调用: torch.nn.MSELoss()

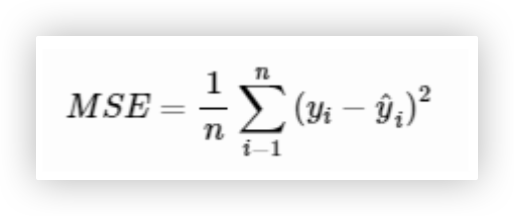
MSELoss, 即均方误差损失函数（Mean Squared Error Loss）, 是深度学习中常用的一种损失函数, 特别是在回归任务中.

MSELoss计算预测值与真实值之间差的平方的平均值, 它对较大的误差更加敏感, 因为误差被平方了.
因此MSELoss对异常值非常敏感, 如果数据集中存在异常值, MSELoss可能会导致模型训练不稳定或过拟合这些异常值.

优点: 在于它能够放大误差, 使得模型在训练过程中更加注重减少大误差的发生, 从而可能提高模型的精度.

MAE

调用: torch.nn.L1Loss()

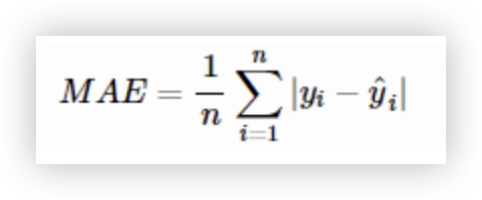
MAE是回归任务中常用的一种损失函数.
它的主要目的是最小化预测值与真实值之间差值的绝对值之和. 它不像MSELoss那样对大的误差赋予过高的权重.

优点: 是对异常值不敏感, 可以在一定程度上抵抗噪声和异常值的影响, 适用于数据分布不均匀的情况.

Huber

调用: torch.nn.SmoothL1Loss()

SmoothL1Loss是L1Loss的一个变种, 这种设计旨在平衡L1Loss和MSELoss的优点.

优点: 在回归问题中表现出良好的性能, 特别是在 [处理异常值] 时比MSELoss更为有效.

---

★ 一点思考

思考一点问题:

分类问题中,有几个类别就会有几个输出,输出的是不同类别的概率.(可以简单这样理解)
如何确定具体是哪个类别,你可以去看看我们自己定义的准确率那个评估指标函数怎么写的.
至于为什么输出层神经元个数和类别数量一致呢,是因为只有引用了激活函数后,才可以基于线性的模型实现分类任务.
回头想想每一个神经元是如何工作额,如何进行前向传播的.引入激活函数的作用是什么？
类别下之前机器学习中, 如何使用线性模型结合sigmod进行分类的, 没有sigmoid线性模型是否可以分类？

1. 那不用显式定义softmax. model(X)这个前向传播返回的值,仅仅只是每个输出神经元加权求和的结果构成的向量.
   这里我们暂且叫作logits. 
   既然如此,在分类场景中,我们定义准确率作为评估指标.会取当前向量中最大值的下标作为该样本的预测类别,为啥可以这么做?
   向量logits中并不是概率呀. 查阅资料,得到的解释是 Softmax 不改变 logits 的相对大小; Softmax 也不改变 logits 的排序.  

2. 也作了一个实验,当我在二分类场景下,显式的在输出层加入了sigmoid或softmax后. 
   model(X)前向传播返回的值.取任意一行. 其和-sigmoid只会把数值调整为0-1的范围内; 其和-softmax 会将他们加起来等于1.

3. 在利用交叉熵计算损失时不需要显式定义 Softmax,它会将输出层输出的向量logits通过softmax处理后得到概率,进而计算损失.
   就像下方这张截图一样!

---