Mnist分类任务
在该篇博客中,我们将用规范化的代码 实现 对图片的分类 (基于MNIST数据集进行手写数字识别).
何为规范化的代码实现呢? 即分批次的进行模型训练.
进一步理解:
- 在前面的章节的示例中,我们都是应用传统机器学习中的
train_test_split对数据集进行切分..
然后设置了迭代次数,循环往复的依照BP算法进行训练 - 思考一个问题, 若数据集样本量特别大,模型若一次性的接收这么大的样本量
模型的训练效率会很低,内存也可能承受不了.
So,为了解决该问题,在迭代训练的过程中,我们需要对样本数据集分批次的进行训练..
PyTorch针对分批次的模型训练, 会利用 TensorDataset +DataLoader 来实现
它不仅可实现分批次, 还可以将样本特征与标签组合到一起,并且进行相关的切分.. 等.
# 样本批次处理
TensorDataset有两方面的功能: 将特征和标签组合、组合多个特征张量
DataLoader有三方面的功能: 批量处理数据、随机打乱数据、多线程加载
TensorDataset + DataLoader 两者组合实现分批次的数据加载和训练.
原理: 简单来说就是将 特征和标签封装到TensorDataset中, DataLoader按批次从TensorDataset中取,便于后续分批参与训练.
import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
# 创建输入图片数据和标签
images = torch.randn(100, 3, 28, 28) # 100张彩色图像,每张图像3通道,28x28像素
labels = torch.randint(0, 10, (100,)) # 100个标签,标签类别的范围在0到9之间
# 创建 TensorDataset >> ★它能将特征和标签整合到一起
dataset = TensorDataset(images, labels)
# 创建 DataLoader >> ★分批次
# - batch_size表示一个批次最多取多少个样本
# - shuffle=False表示没有打乱,按顺序取; shuffle=True表示打乱
# 通常我们都会设置为True,数据会被随机打乱,确保模型不会受到数据顺序的影响
# - num_workers表示启动4个线程,4个工人并行加载数据进行分批次; 若不加该参数,则证明只有一个工人在分批次
loader = DataLoader(dataset, batch_size=32, shuffle=True, num_workers=4)
# 通过遍历 `loader`,我们可以轻松地获取每个批次的特征和标签
# - batch_features是某一批次的特征,batch_labels是某一批次的标签
for batch_features, batch_labels in loader:
print(f"Batch Features Shape: {batch_features.shape}")
print(f"Batch Labels Shape: {batch_labels.shape}")
"""
Batch Features Shape: torch.Size([32, 3, 28, 28])
Batch Labels Shape: torch.Size([32])
Batch Features Shape: torch.Size([32, 3, 28, 28])
Batch Labels Shape: torch.Size([32])
Batch Features Shape: torch.Size([32, 3, 28, 28])
Batch Labels Shape: torch.Size([32])
Batch Features Shape: torch.Size([4, 3, 28, 28])
Batch Labels Shape: torch.Size([4])
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
补充1:上述代码, 通过 dataset[0], 我们可以访问第一个样本的图像特征和标签..
# 通过dataset[0]取到第一个样本数据(包含特征和对应标签 -- 即图片和对应类别)
# sample_feature1, sample_feature2 = dataset[0]
type(dataset[0]) # tuple
type(dataset[0][0]) # torch.Tensor
type(dataset[0][1]) # torch.Tensor
dataset[0][0].shape # torch.Size([3, 28, 28])
dataset[0][1] # tensor(9)
1
2
3
4
5
6
7
2
3
4
5
6
7
补充2: 就TensorDataset而言,它除了将特征和标签组合,还可以将多个特征张量组合在一起.
假设我们有两个不同的特征张量, 我们可以将它们组合成一个 TensorDataset
import torch
from torch.utils.data import TensorDataset
# 创建两个特征张量
feature1 = torch.randn(100, 50) # 100个样本,每个样本特征维度是50维
feature2 = torch.randn(100, 30) # 100个样本,每个样本特征维度是30维
# 创建 TensorDataset
dataset = TensorDataset(feature1, feature2)
# 访问数据集中的特定样本
sample_feature1, sample_feature2 = dataset[0]
print(f"Sample Feature1 Shape: {sample_feature1.shape}") # 输出: Sample Feature1 Shape: torch.Size([50])
print(f"Sample Feature2 Shape: {sample_feature2.shape}") # 输出: Sample Feature2 Shape: torch.Size([30])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
# Mnist项目-手写数字识别
MNIST项目是 一个深度学习领域的经典入门项目, 基于MNIST数据集进行手写数字识别
MNIST数据集是一个大型的手写数字数据库, 由美国国家标准与技术研究所（NIST）提供.
这个数据集包含了50,000个训练样本和10,000个测试样本, 每个样本都是28x28像素的灰度图像, 对应着从0到9的数字.
由于其简单性和广泛的应用性, MNIST数据集成为了深度学习初学者的首选项目之一.
# 网络结构设计
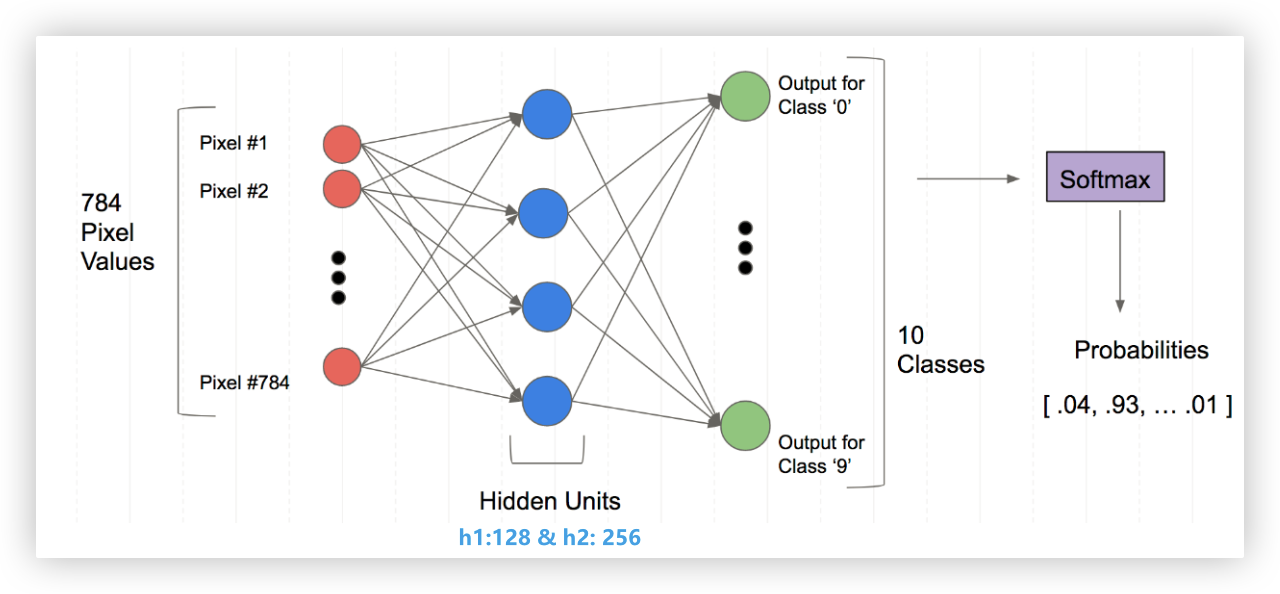
- 输入层: 784个神经元
- 隐藏层: 128神经元
- 隐藏层: 256神经元
- 输出层: 10个神经元, 为图片分到每个数字的概率
1.每个样本都是28x28像素的灰度图像 -- 输入层:784个神经元
2.可以设置任意多个隐藏层,每个隐藏层可以有任意个神经元,一般隐藏层神经元个数设置为8或32的整数倍
3.数据集的标签对应从0到9的数字 -- 输出层: 10个神经元 > 每个样本都有10个输出,简单理解就是该样本对应10个类别的概率
28*28的二维数组展平为竖着的784*1的列向量
784*1的列向量通过加权求和以及激活函数变换为128*1的列向量 > 特征提取的过程
128*1的列向量通过加权求和以及激活函数变换为256*1的列向量 > 特征提取的过程
256*1的列向量通过加权求和以及激活函数变换为10*1的列向量 > 哪个成员最大,对应的下标就是识别的结果
Q:思考一个问题,在784*128这个线性层中,包含了多少个w和b参数?
A: w参数 - 连线的个数,784×128=100352
b参数 - 隐藏层神经元的个数 128个
注意:最后一步是否加上softmax函数,应根据对应使用的损失函数来决定.
使用交叉熵,不用加;使用负对数交叉熵,要加!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 迭代分批次训练思路
- 外层循环: 进行10次迭代/内层代码执行10次 (注意!!每开始一次新的迭代,这里列表都会初始化为空列表)
batch_loss = [],batch_acc=[]
batch_loss_test = [],batch_acc_test=[]
这些列表用于存储当前迭代中,测试集和训练集每个小批次的损失和准确率
- 内层代码 有两个for循环
> 训练
1.训练阶段for循环遍历得到训练集中每个小批次的样本集
2.每个小批次都将经历一次BP算法的过程,完成前向传播、损失计算、反向传播和参数更新
下一个小批次用的是上一个小批次更新的w参数
3.记录训练集每个小批次的损失和准确率 放在 batch_loss、batch_acc中
> 测试 - 测试阶段是不进行反向传播和权重更新的
1.训练阶段for循环遍历得到训练集中每个小批次的样本集
2.基于当前迭代训练得到的w参数进行一次前向传播,得到该批次测试样本的分类结果
3.记录测试集每个小批次的损失和准确率 放在 batch_loss_test、batch_acc_test中
> 当迭代次数是2的倍数时,求当前 损失-batch_loss列表 和 准确率-batch_acc列表的平均值
当迭代次数是2的倍数时,求当前 损失-batch_loss_test列表 和 准确率-batch_acc_test列表的平均值
!!! 综上,明确两点,整个代码流程就明了了:
- 训练时,每个小批次都会更新权重w,下一个小批次用的是上一个小批次更新后的权重.
- 每次新迭代权重会继续基于上一次迭代最终更新的权重开始训练.
★ 每一次迭代的最终的权重是该次迭代训练集的最后一批次更新的权重!
Q:每次迭代以及每次迭代中训练集的每一批次的w都是最新的,那为啥要基于当前迭代中每一批次的损失和准确率,打印它们的平均值
A:查阅资料,说的是一个迭代(epoch)的平均损失可以反映模型在当前epoch内的总体表现
若我们使用当前迭代训练的最后一个批次的损失和准确率,难免会有误差.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
ps: 这里训练集5万个数据,测试集1万个数据, 每批次是64个.. 那么不难算出,每次迭代后,都是下面这个情况
batch_loss和batch_acc的长度都为50000/64=782; batch_loss_test的长度都是10000/64=157..
# 代码呈现
- 准备数据集 数据集分为了 [训练集特征与标签] 和 [测试集特征与标签]
- 基于上面"网络设计结构"的分析,构建网络模型
- 将numpy类型的数据集进行数据类型转换,转换成tensor类型
- 自定义评估指标函数, 准确率作为分类评估指标
- 定义损失函数和优化器
- 将特征和标签封装到TensorDataset中, 再利用DataLoader分批次,后续通过for循环来取
- 基于上面"迭代分批次训练思路"的分析,来编写代码
数据准备
import pickle
import gzip
from pathlib import Path
path = "./data/mnist/mnist.pkl.gz"
# 读取压缩文件数据
with gzip.open(path, "rb") as f:
# (x_train, y_train) >> 训练集数据; (x_valid, y_valid) >> 测试集数据; _ >> 验证集(可忽略)
# 都是numpy数据类型
(x_train, y_train), (x_valid, y_valid), _ = pickle.load(f, encoding="latin-1")
# x_train 有50000张图片,每张图片有784个特征 >> 784=28*28 即它将一张灰度图片(二维)展平为一维的向量
print(x_train.shape,y_train.shape,set(y_train)) # (50000, 784) (50000,) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
print(x_valid.shape,y_valid.shape) # (10000, 784) (10000,)
import matplotlib.pyplot as plt
img = x_train[0] # 取出训练集中的第一张图片
print(img.shape) # (784,)
img = img.reshape((28, 28)) # (784,)变形成(28,28)
plt.imshow(img,cmap="gray") # 像素比较低,所以看起来很模糊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
神经网络架构
import torch
import torch.optim as optim
import numpy as np
from torch import nn
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
# - 构建网络模型
class Mnist_NN(nn.Module):
def __init__(self):
super().__init__()
self.hidden1 = nn.Linear(784, 128) # 输出层与隐藏层之间的线性层
self.hidden2 = nn.Linear(128, 256) # 隐藏层与隐藏层之间的线性层
self.out = nn.Linear(256, 10) # 隐藏层与输出层之间的线性层
def forward(self, x):
o1 = torch.relu(self.hidden1(x)) # 将x输入到 输出层与隐藏层之间的线性层,对该线性层的输出使用relu激活
o2 = torch.relu(self.hidden2(o1))
y = self.out(o2)
return y
model = Mnist_NN().to(device)
"""
Mnist_NN(
(hidden1): Linear(in_features=784, out_features=128, bias=True) # 输出层与隐藏层之间的线性层
(hidden2): Linear(in_features=128, out_features=256, bias=True) # 隐藏层与隐藏层之间的线性层
(out): Linear(in_features=256, out_features=10, bias=True) # 隐藏层与输出层之间的线性层
)
"""
# - 数据类型转换,numpy->tensor tensor才可以应用到gpu中
x_train, y_train, x_valid, y_valid = map(torch.tensor, (x_train, y_train, x_valid, y_valid))
# - 准确率作为分类评估指标 基本原理:模型输出层输出的10个概率中最大值对应的下标就是该样本的预测结果
def accuracy(outputs, labels):
_, predicted = torch.max(outputs, 1)
correct = (predicted == labels).sum().item()
total = labels.size(0)
return correct / total
# - 定义损失函数和优化器
criterion = nn.CrossEntropyLoss() # 交叉熵作为损失函数,则输出层无需配置softmax
opt = optim.Adam(model.parameters(), lr=0.001) # 优化器Adam
# - 将特征和标签封装到TensorDataset中, 再利用DataLoader分批次,后续通过for循环来取
bs = 64 # 一个批次64个样本
train_ds = TensorDataset(x_train, y_train)
test_ds = TensorDataset(x_valid, y_valid)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
test_dl = DataLoader(test_ds, batch_size=bs, shuffle=True)
def train_(step):
# 存储每批次训练后的损失和正确率
batch_loss = []
batch_acc = []
# 批次训练
for xb,yb in train_dl: # 基于batch开始一次迭代
# 训练数据加入到mps中,就可使用gpu
xb = xb.to(device)
yb = yb.to(device)
# 一次bp算法过程
prediction = model(xb) # 向前传播
loss = criterion(prediction, yb) # 计算损失
loss.backward() # 反向传播
opt.step() # 更新参数
opt.zero_grad() # 梯度清零
# 每批次损失记录到batch_loss数组中
batch_loss.append(loss.item())
# 训练集准确率
train_acc = accuracy(prediction, yb)
# 每批次准确率记录到batch_acc数组中
batch_acc.append(train_acc)
# 每2次迭代打印一次训练的损失和准确率
if (step+1) % 2 == 0:
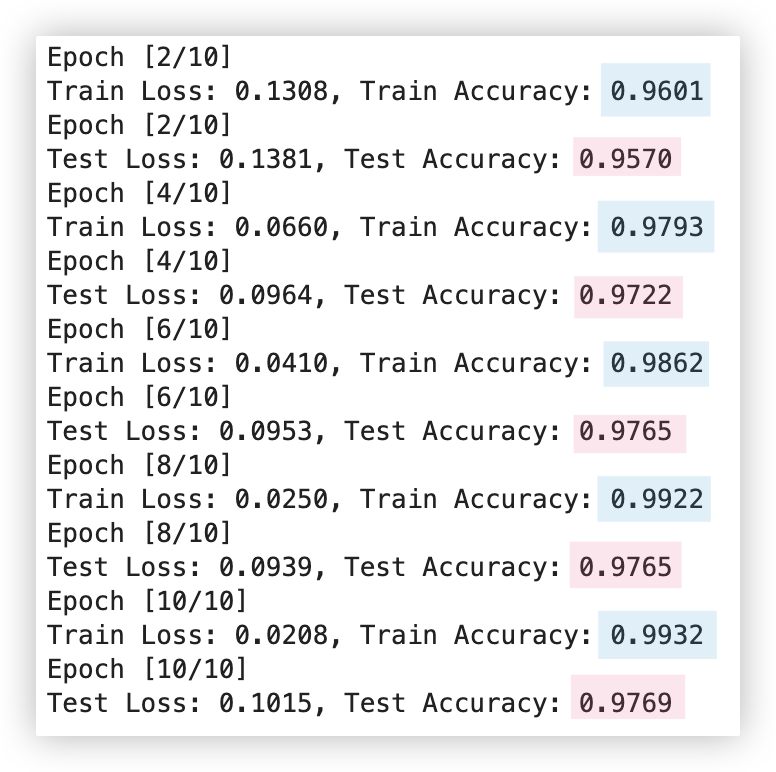
print(f'Epoch [{step+1}/{num_epochs}]')
print(f'Train Loss: {np.mean(batch_loss):.4f}, Train Accuracy: {np.mean(batch_acc):.4f}')
def test_(step):
# 存储每批次测试后的损失和正确率
batch_loss_test = []
batch_acc_test = []
# 批次测试
for xb,yb in test_dl: # 基于batch开始一次迭代
# 测试数据加入到mps中,就可使用gpu
xb = xb.to(device)
yb = yb.to(device)
with torch.no_grad(): # 不计算梯度,提升运行效率
test_outputs = model(xb) # 基于测试集特征的分类结果
test_loss = criterion(test_outputs, yb) # 测试集损失
# 每批次损失记录到batch_loss_test数组中
batch_loss_test.append(test_loss.item())
# 测试集准确率
test_acc = accuracy(test_outputs, yb)
# 每批次准确率记录到batch_acc_test数组中
batch_acc_test.append(test_acc)
# 每2次迭代打印一次训练的损失和准确率
if (step+1) % 2 == 0:
print(f'Epoch [{step+1}/{num_epochs}]')
print(f'Test Loss: {np.mean(batch_loss_test):.4f}, Test Accuracy: {np.mean(batch_acc_test):.4f}')
# - 多迭代多批次的 训练&测试 网络模型 外层for循环>>迭代;内存for循环>>批次
num_epochs = 10 # 10次迭代
for step in range(num_epochs):
# ■ 训练阶段
model.train()
train_(step)
# ■ 测试阶段
model.eval()
test_(step)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
可以看到,不管是训练集还是测试集. 根据迭代次数的不断增加,准确率整体是呈现上升趋势的..
ps: 若增加迭代次数,发现准确率变化很小,可以设置一个阀值用于停止迭代训练 -- 相关思路 > 早停法.
这是解决过拟合的一种措施.emmm
