 激活函数
激活函数
关于神经网络的架构, ★ 精简下来就两句话:
- 在一个神经网络架构中, 除了输入层没有激活函数外, 其他的网络层(隐层和输出层)的每一个神经元都会包含一个激活函数.
- 神经元接收来自其他神经元或外部源的输入(xi), 每个输入都有一个相关的权值 (wi).
它是根据该输入对当前神经元的重要性来确定的.
对该输入信号加权求和后(汇总信号), 经过一个激活函数 f 处理后, 计算得到该神经元的输出.
# 激活函数的作用
在神经网络的架构中为何要使用激活函数呢? 激活函数的作用到底是什么?
若我们在神经网络的架构中, 不使用激活函数, 那么每个节点仅仅就是对输入信号的加权求和..
无论神经网络有多少层, 最终输出层的结果是 线性组合的结果..
引入非线性函数作为激活函数, 那输出就不再是线性组合的结果了, 而是可以逼近 [任意函数] 的 [线性] 和 [非线性] 的结果.
所以, 在神经元中引入了激活函数, 其本质就是向神经网络中引入非线性因素. 即通过激活函数神经网络就可以拟合各种曲线
如何进一步理解上面这段话呢? 你可以这样想:
预测房间, 楼层、采光率与价格之间的关系,是线性的;
但当特征维度很多时, 真实场景下, 绝大概率处理的问题都很复杂, 都是非线性的组合.. 所以神经网络中不得不加 激活函数..
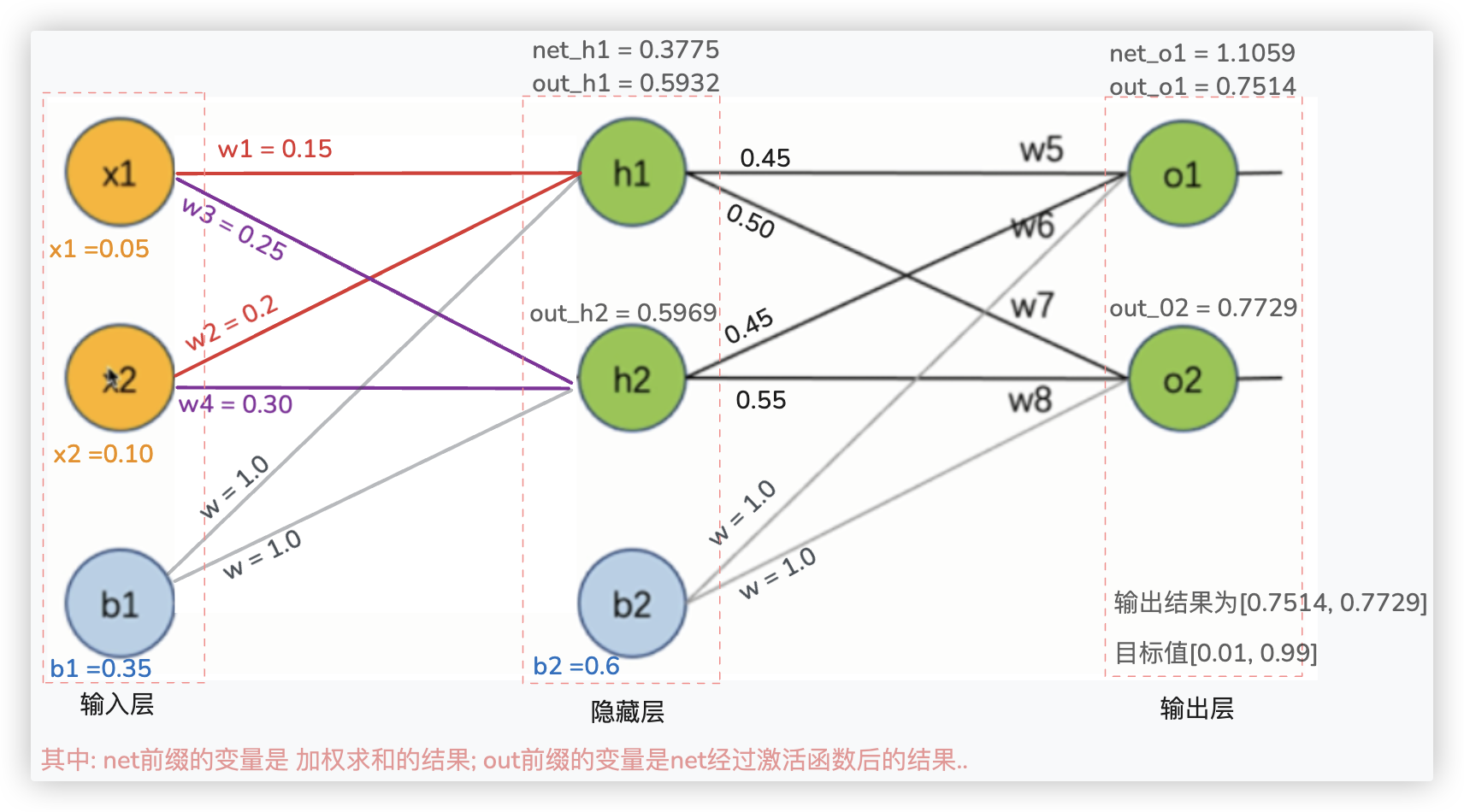
提一嘴: 不难理解, 像上面图中的out_o1是经过非线性激活函数 sigmoid 求得的结果, 则 out_o1 的值是满足非线性分布的..
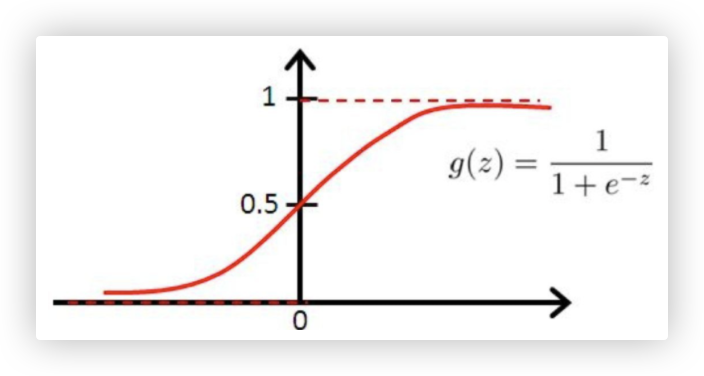
Ps: 该图像是sigmoid激活函数, 我们早在传统机器学习的逻辑回归中就遇到过了..
提示一点, 激活函数大部分是非线性函数, 但也有些激活函数是线性的..
# 梯度消失
以下描述以sigmoid激活函数为例
回顾下, 反向传播过程中 总损失对w5参数的更新.. 涉及到了下面这个链式公式:

我们重点关注下outo1, 它是sigmoid激活函数返回的结果, sigmoid激活函数是非线性的, 则证明 outo1的值也是满足非线性分布的..
我们根据sigmoid激活函数的函数图像和导数图像进一步分析:
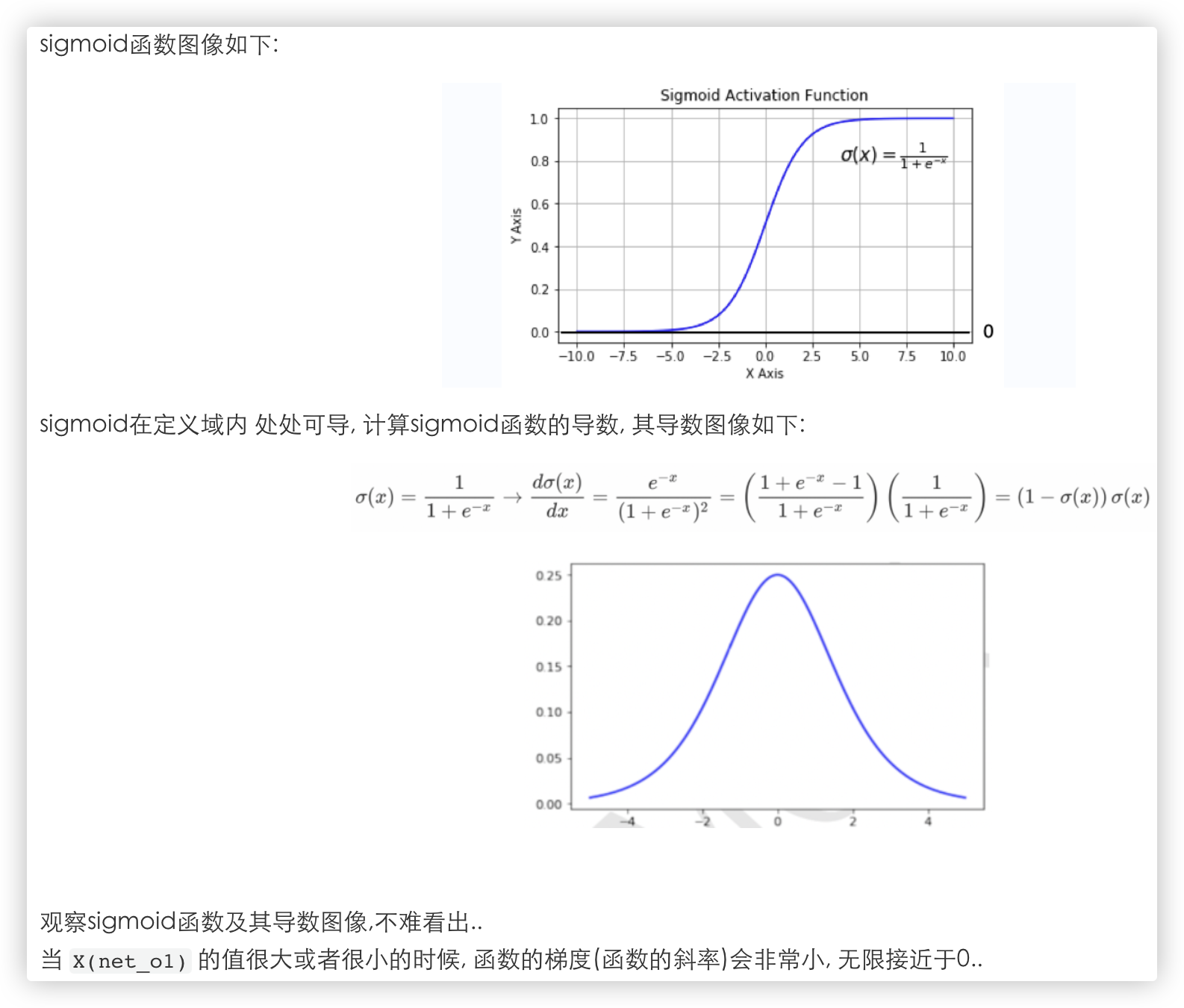
结合上述分析对梯度消失进行解释:
- 根据sigmoid的导数图像可知,不管怎么样,sigmod的导数都是一个小于1的值.
- 反向传播中每一层的梯度依赖于上一层梯度的乘积.
如果激活函数(如 sigmoid) 的导数小于 1, 且网络层数较多时, 梯度会呈指数级减小, 导致前几层几乎无法更新参数.
这种现象被称为梯度消失.
回顾下, 反向传播过程中 总损失对w1参数的更新 就明白了..

截图中, 乘积的每一项都是求偏导, 用红色标注的out_o1和out_h1都是经过sigmoid函数输出的结果..
示例中只有3层, 若中间加了很多隐层, 最终神经网络有10层呢?
由于sigmoid导数的值在(0, 0.25]之间, 大胆假设都为0.2 (有红色标注的那几项), 0.2*0.2*0.2... 最终的梯度将趋近于 0.
这会导致反向传播过程中, 前面几层(如 w_1, w_2 )几乎无法更新, 学习过程变得极其缓慢.
# 梯度爆炸
梯度消失, 我们理解了, 那么梯度爆炸呢? 同样的道理.
当我们使用sigmoid作为激活函数时,它的导数取值范围都是小于1.
反向传播过程中,会导致向低层传递的梯度也变得非常小.所以会产生梯度消失的问题!
Q:啥叫低层传递. A:计算了w5后,计算w1. w1比w5的层数低,而且计算w1时,会用到w5这一层的梯度.
那么我们可能会想到,如果使用导数大于1的函数作为激活函数,情况会如何?
在反向传播的过程中,如果某个激活函数导致了向低层传递的梯度也变得很大.
在一层一层反向传播的时候,每传播一层学习梯度就会变大一点,经过多层传播后,梯度会接近于无穷大,从而使得权值W调整接近于无穷大.
那么就意味着该层的参数,处于一种极不稳定的状态,那么网络就不能正常工作了.此时网络参数很难得到有效训练.
这种现象被称为梯度爆炸.
2
3
4
5
6
7
8
9
# 常见的激活函数
# sigmoid 函数
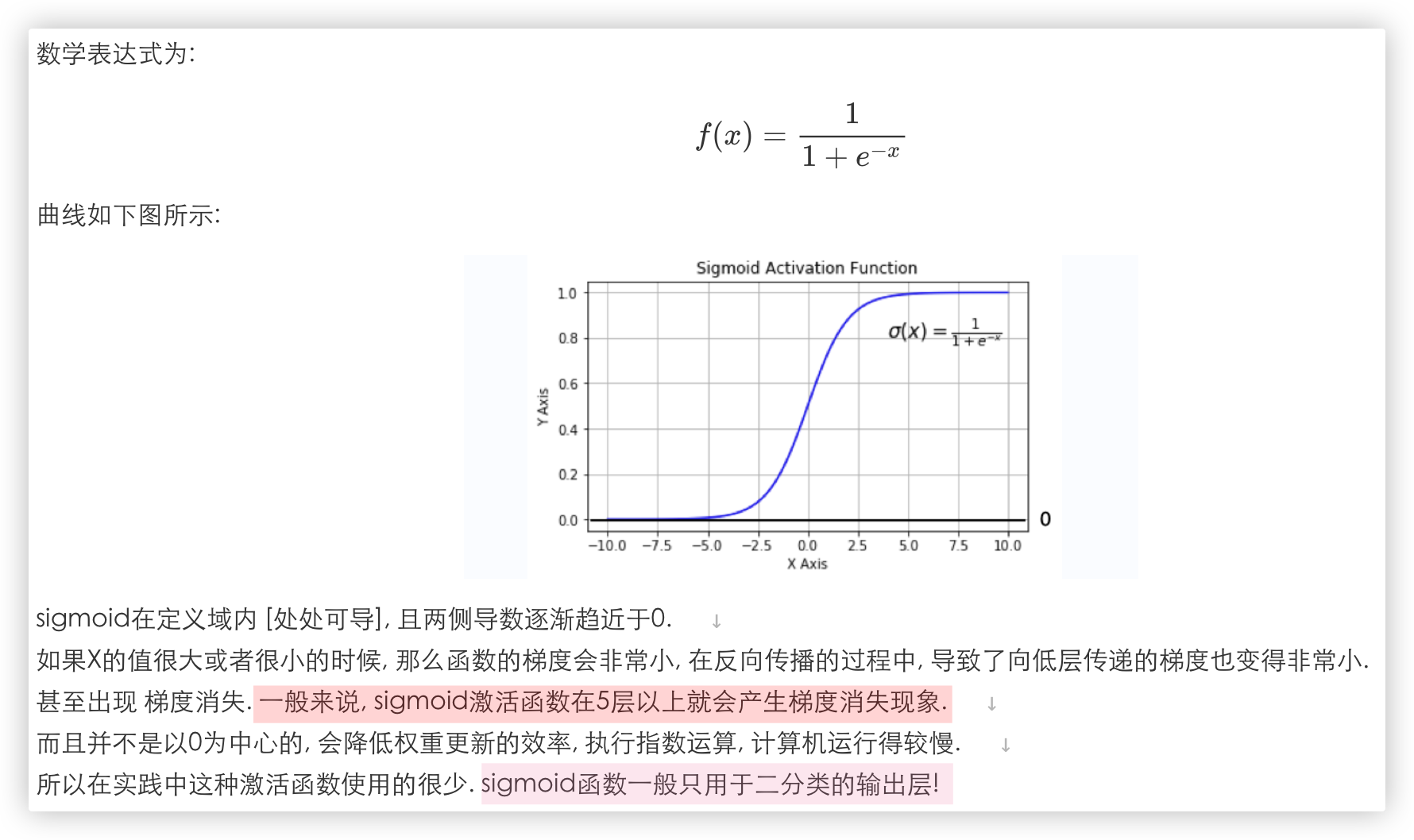
在我们的实践过程中, 我们不会在隐层中使用sigmoid作为激活函数, sigmoid一般作用于输出层, 解决二分类的问题..
因为隐层使用激活函数会导致梯度消失, 梯度消失会 造成 网络参数难以得到有效的训练..
# tanh(双曲正切曲线)
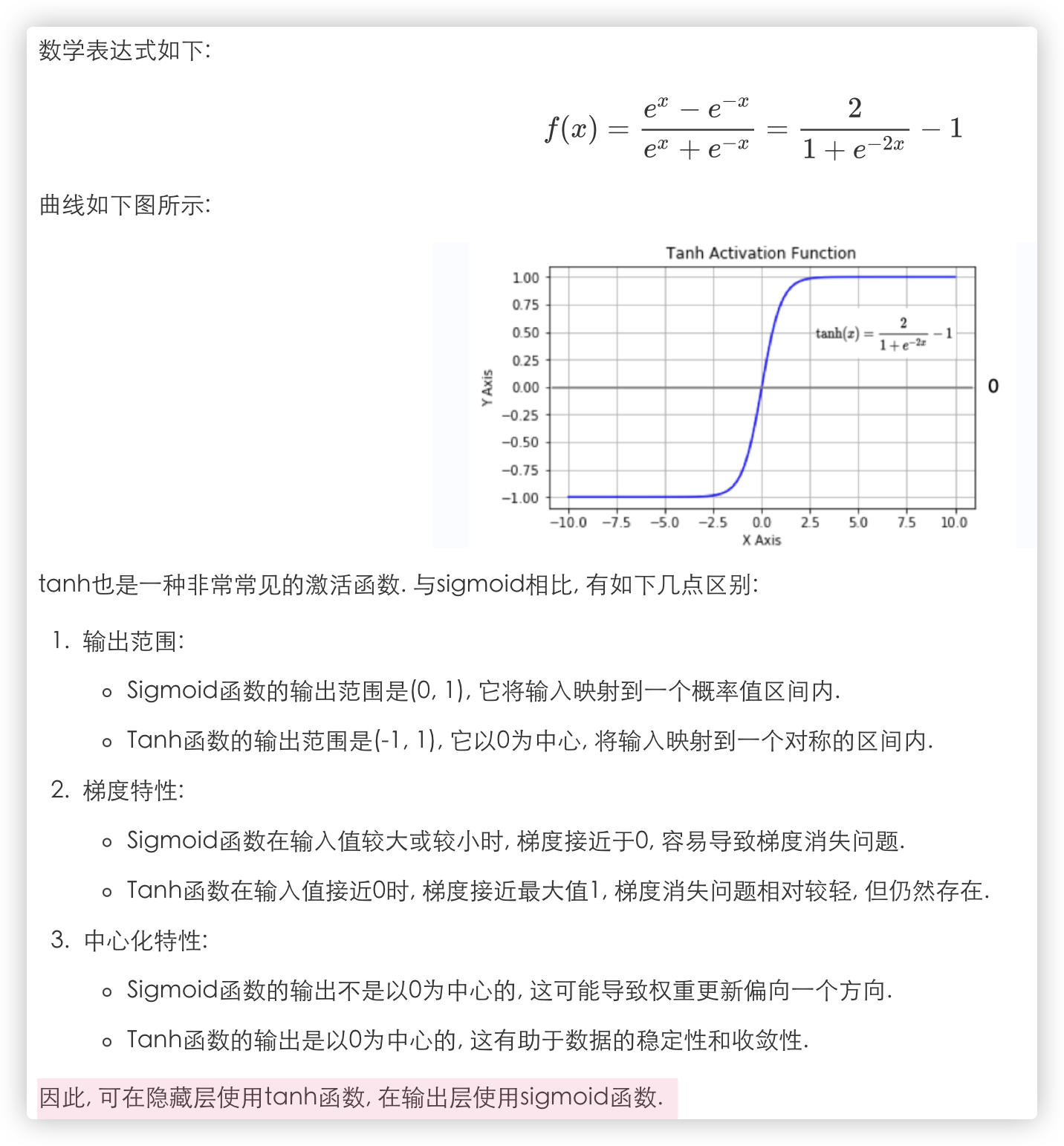
# ReLu
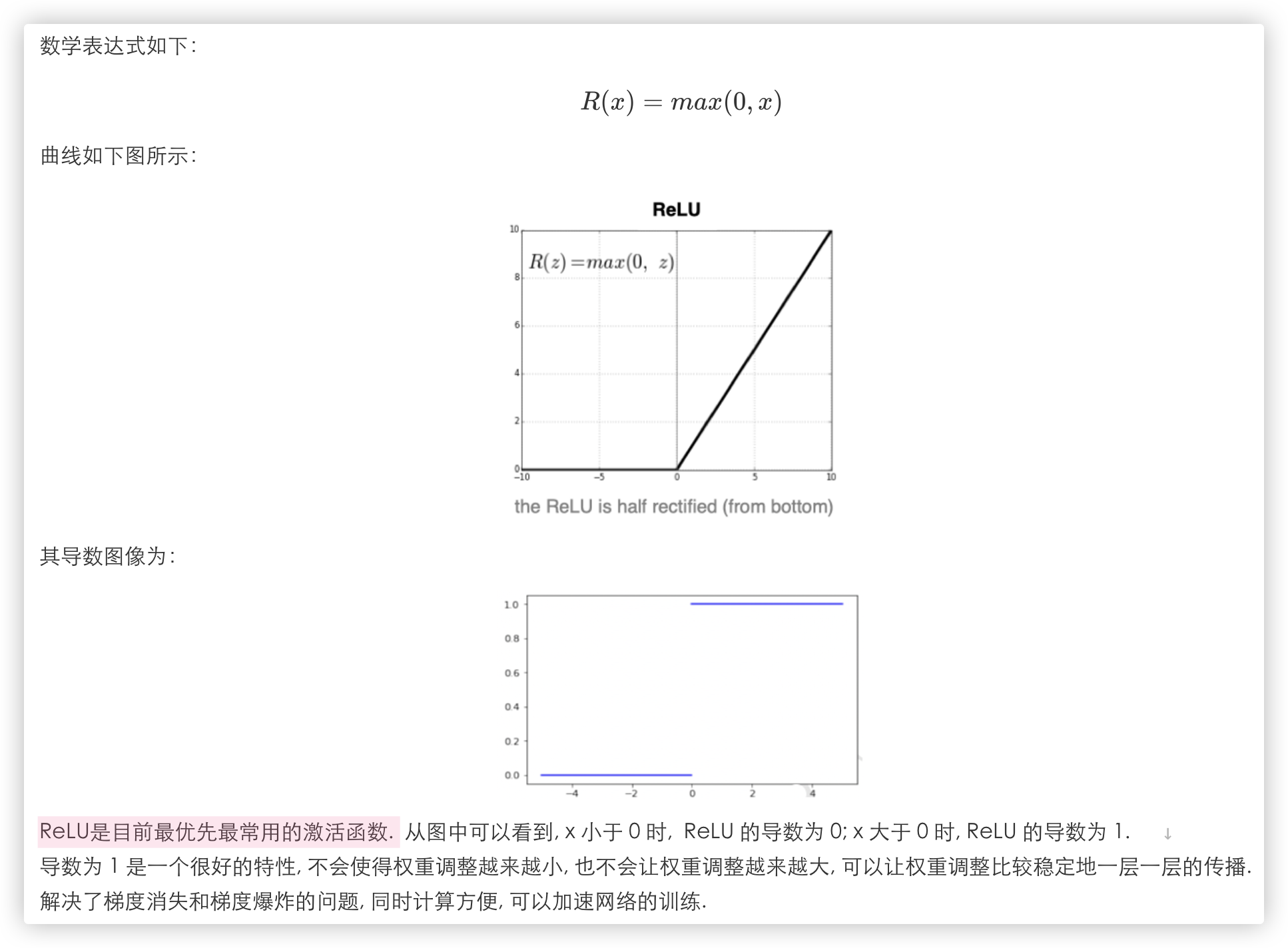
Q: 思考 (¯﹃¯)
ReLU 函数看起来是挺好的, 既是非线性函数, 导数又为 1, 但是它好像也存在一些问题.
当 x 小于 0 时, ReLU 函数输出为 0, 导数也为 0, 有些信号不就丢失掉了吗?
(意思是 反向传播过程中, ReLU求导为0, 导致某一层的权值无法更新, 以及该层往后更底层的权值都无法更新)
确实是丢失了一些信号,但是没关系.
因为在神经网络中,有些信号是冗余的,也就是说其实网络最后在做预测的时候并不需要从前面传过来的所有的信号.
实际上只需要一部分的信号,网络就可以进行预测. 并且使用部分信号来进行预测与使用全部信号来进行预测得到的结果相差不大!
2
3
4
# Leaky_ReLU
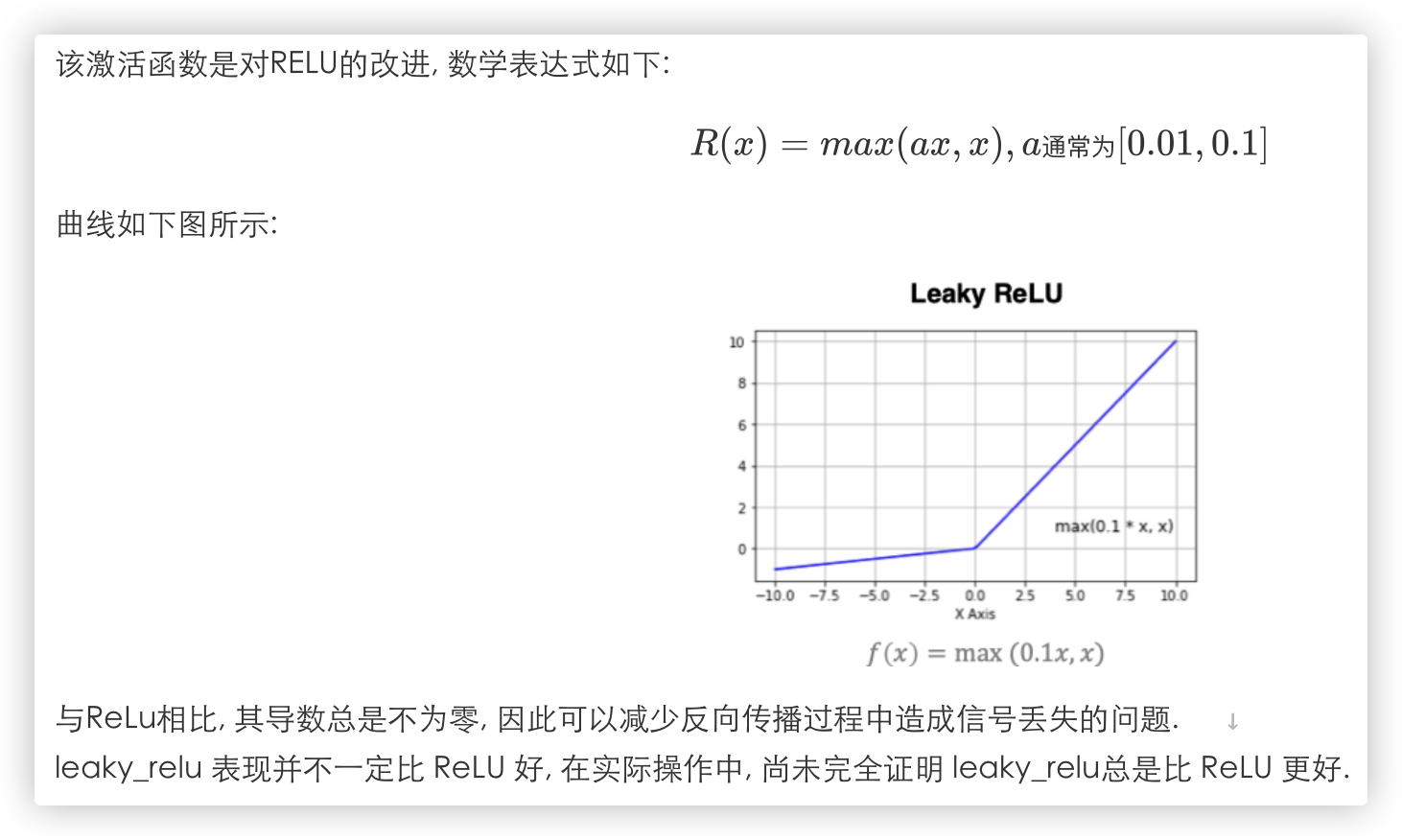
# SoftMax
在传统机器学习的 逻辑回归的多分类任务中, 我们就接触过这个激活函数.

# 如何选择激活函数?
隐藏层
- 优先选择ReLU激活函数
- 如果ReLU效果不好, 那么尝试其他激活, 如Leaky ReLu等.
- 不要使用sigmoid激活函数, 可以尝试使用tanh激活函数.
输出层
- 二分类问题选择sigmoid激活函数
- 多分类问题选择softmax激活函数
问题: 有专门应用于回归任务的激活函数吗?
对于回归问题, 输出层通常不使用激活函数, 或者使用线性激活函数( 即 f(x) = x ).
这样可以使得模型的输出值可以覆盖实数域, 对于隐藏层, 可以使用常用的激活函数, 如 ReLU、sigmoid 或 tanh 等.
