递归_查找
程序 = 数据结构 + 算法
1,"123"等数据用列表、字典等数据结构存放起来. 但都是静态的,用函数等写成算法让这些数据活跃起来.
1
2
2
# 复杂度
# 时间复杂度
时间复杂度是用来估计算法运行时间的一个式子.(单位).
n = 64
while n > 1:
print(n)
n = n // 2
"""
2^6 = 64 --> log2^64=6 --> 则时间复杂度记为 O(log2^n) 或者 O(log^n)
★ 当算法过程中出现循环折半的时候,时间复杂度式子中会出现logn. (每次循环迭代 让问题的规模缩小一半)
"""
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
常见的时间复杂度 (复杂度从低到高,效率从高到低)
Ps: 一般情况下是这样的,现实中还要考虑机器和问题的规模!
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^2logn) < O(n^3)
其它: O(n!) O(2^n) O(n^n)
分析:
O(n) 和 O(nlogn),同时约去一个n,就是O(1) 和 O(logn)
因为O(1) < O(logn),So,O(n) < O(nlogn),其余同理.
1
2
3
4
5
6
2
3
4
5
6
如何简单快速地判断算法复杂度??
▲ 快速判断算法复杂度(适用于绝大多数简单情况)
1> 确定问题规模
2> 是否有循环减半过程 -- logn
3> 若有k层关于n的循环 -- n^k
▲ 复杂过程,根据算法执行过程判断
1
2
3
4
5
2
3
4
5
# 空间复杂度
空间复杂度是用来评估算法内存占用大小的式子
空间复杂度的表示方法与时间复杂度完全一样
算法使用了几个变量 O(1)
算法使用了长度为n的一维列表 O(n)
算法使用了m行n列的二维列表 O(mn)
我们更看重用户等待的时间,通常会用"空间换时间" eg:分布式计算
1
2
3
4
5
2
3
4
5
# 递归
递归的两个特点: 调用自身 、 结束条件
# 递归回顾
"""
分析:
func1没有结束条件
func2看似有结束条件,但不会结束的.
func3、func4是递归!
若x=3.分别调用fun3(x)、func4(x).输出结果分别为:
func3(3) -- 3 2 1
func4(3) -- 1 2 3
"""
def func1(x):
print(x)
func1(x - 1)
def func2(x):
if x > 0:
print(x)
func2(x + 1)
def func3(x):
if x > 0:
print(x)
func3(x - 1)
def func4(x):
if x > 0:
func4(x - 1)
print(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
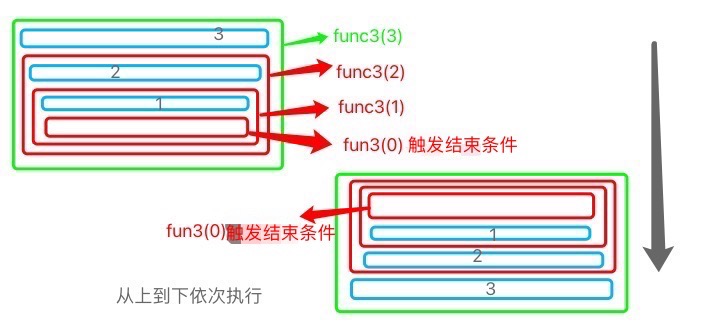
Ps: 图中大框表示函数的执行,里面的蓝色小框表示print语句..
# 汉诺塔问题
有三根杆(编号A、B、C), 在A杆自下而上、由大到小按顺序放置64个金盘.
游戏的目标: 把A杆上的金盘全部移到C杆上, 并仍保持原有顺序叠好.
操作规则:
每次只能移动一个盘子;
在移动过程中三根杆上都始终保持大盘在下, 小盘在上;
操作过程中盘子可以置于A、B、C任一杆上.
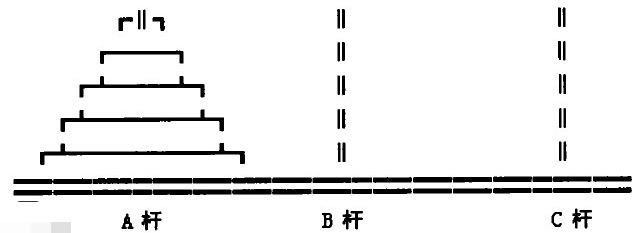
分析:
> n = 2时
1.把小圆盘从A移动到B
2.把大圆盘从A移动到C
3.把小圆盘从B移动到C
> n个盘子时,可以将其看作是两个整体,第n个盘子为一个整体、其余的n-1个盘子为一个整体,使得问题的规模减1.
1.把n-1个盘子经过C移动到B
2.把第n个盘子移动到C
3.把n-1个盘子从B经过A移动到C
假设移动n个盘子,需要h(n)步.
那么根据上面移动n个盘子时候的步骤,h(n) = h(n-1)+1+h(n-1) = 2h(n-1)+1
也就是 f(x) = 2f(x-1) +1, 该数据模型走势类似于 2^n
So,2^64=18446744073709551616
假设每秒移动一个盘子,大概需要5800亿年.Wow～
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
代码实现:
# n,a,b,c表明将n个盘子从a经过b移动到c
# 四个参数:多少个盘子,从哪里、经过哪里、到哪里
def hanoi(n, a, b, c):
if n > 0:
hanoi(n - 1, a, c, b)
print(f"moving from {a} to {c}")
hanoi(n - 1, b, a, c)
hanoi(3, 'A', 'B', 'C')
"""
moving from A to C
moving from A to B
moving from C to B
moving from A to C
moving from B to A
moving from B to C
moving from A to C
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 查找
在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程.
针对有序列表,二分查找的效率要比线性查找的效率高!
# 顺序查找
顺序查找(Linear Search): 也叫线性查找, 从列表的第一个元素开始,顺序进行搜索,直到找到元素或搜索到列表最后一个元素为止.
时间复杂度 O(n)
列表查找(线性表查找): 从列表中查找指定元素
输入 - 列表、待查找元素
输出 - 元素下表 (未找到元素时,一般返回None或-1)
内置的列表查找函数: index() -- 它的本质是线性查找!!
def linear_search(li, target):
for ind, val in enumerate(li):
if val == target:
return ind
return None
print(linear_search([1, 4, 6, 4], 4)) # 1
"""
分析:该问题的时间复杂度为多少?
问题规模是列表的长度n;没有循环减半过程;有一层循环.
So,该程序的时间复杂度为 O(n)
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
# 二分查找
二分查找(Binary Search): 也叫折半查找.
从有序列表的 初始 候选区li[0:n]开始, 通过对 待查找的值 与 候选区 中间值的比较,可以使候选区减少一半.
时间复杂度 O(logn)
Ps: 候选区的意思就是在该区域里查找待查找的值..
- 从列表my_list=[1,2,3,4,5,6,7,8,9]中查找元素3!!
用left和right两个变量来维护候选区.它们的值指代元素的下标.
▲ 初始状态.
此时,left=0、 right=len(my_list)-1即right=8、 列表中间元素的下标/位置mid=(left+right)//2 即mid=4
1 2 3 4 5 6 7 8 9
⬆️ ⬆️ ⬆️
left "mid" right
进一步分析:
my_list[mid]=5 > 3 说明,待查找的值在mid的左边,即my_list[left:mid]之间
Ps:列表切片是顾头不顾尾的.因而没有mid-1 在左边应保证列表切片包含left位置所在的元素
So,将right移动到下述位置,此时right=mid-1
1 2 3 4 5 6 7 8 9
⬆️ ⬆️ ⬆️
left right
▲ 更新mid
mid=(0+3)//2=1
1 2 3 4 5 6 7 8 9
⬆️ ⬆️ ⬆️
left "mid" right
进一步分析:
my_list[mid]=2 < 3 说明,待查找的值在mid的右边,my_list[mid+1:right+1]之间 (或者这样写my_list[mid+1:])
Ps:列表切片是顾头不顾尾的. 在右边应保证列表切片包含right位置所在的元素,所以这里切片中right+1
So,将left移动到下述位置,此时left=mid+1
1 2 3 4 5 6 7 8 9
⬆️ ⬆️ ⬆️
left right
▲ 更新mid
mid=(2+3)//2=2
1 2 3 4 5 6 7 8 9
⬆️ ⬆️
left right
⬆️
mid
进一步分析:
my_list[mid]=3 So,结果为2.
思考下,查不到的情况,是如何结束算法的呢.
假如,my_list[2]的值不是3,是4..
1 2 4 4 5 6 7 8 9
⬆️ ⬆️
left right
⬆️
"mid"
按照前面的逻辑,接着判断,4>3证明查找的值在mid的左边,则right=mid-1
1 2 4 4 5 6 7 8 9
⬆️ ⬆️
right left
此时right的值小于left,证明找不到,算法结束!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
代码实现:
def binary_search(li, val):
left = 0
right = len(li) - 1
while left <= right:
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] > val: # 待查找的值在mid的左侧
right = mid - 1
else: # li[mid] < val 待查找的值在mid的右侧
left = mid + 1
return None
li = [1, 2, 3, 4, 5, 6, 7, 8]
print(binary_search(li, 3))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Ps: 还有种方法是用 递归 来实现.在python面向对象/06_函数进阶.md 里有递归二分法的实现!
# 效率验证
import time
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print(f"{func.__name__} running time:{t2 - t1} secs.")
return result
return wrapper
@cal_time
def linear_search(li, target):pass
@cal_time
def binary_search(li, val):pass
li = list(range(10000))
linear_search(li, 2345)
binary_search(li, 2345)
"""
linear_search running time:0.00041604042053222656 secs.
binary_search running time:1.6927719116210938e-05 secs. # e-05 科学记数法
"""
# 注:计算机一般一秒的运算次数是 10^7 = 1千万次;
# 那么时间复杂度为O(n^2)的程序,若n等于10000,则大概需要10000*10000/10000000=10S左右的运算时间!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33