softmax多分类器
在逻辑回归模型中, 应用 Sigmoid 函数能够完成二分类任务.
在SoftMax多分类器模型中, 主要依赖 Softmax 函数, 进而实现多分类的功能.
# softmax函数详解
- 通过上面截图的推导过程,可以看到,softmax跟sigmoid一样, 都是将(-∞,+∞)映射到(0,1)之间.
不同的是 sigmoid输入的是一个值, softmax输入的是一个数组,数组里有多个值 - ★ 数组经过softmax处理后, 数组中的每个元素具有以下三个特征:
- 0 < 每个元素 < 1
- 每个元素相加之和等于1
- Q 思考: 输入的a与返回的softmax(a)之间的关系?
A 原先在a数组中最大的,经过softmax后依旧是最大的. 最小的、不大不小的同理. 位置是不变的.
用代码来简单验证下, 数组a = [1,3,5], 对其数组a进行softmax的操作.
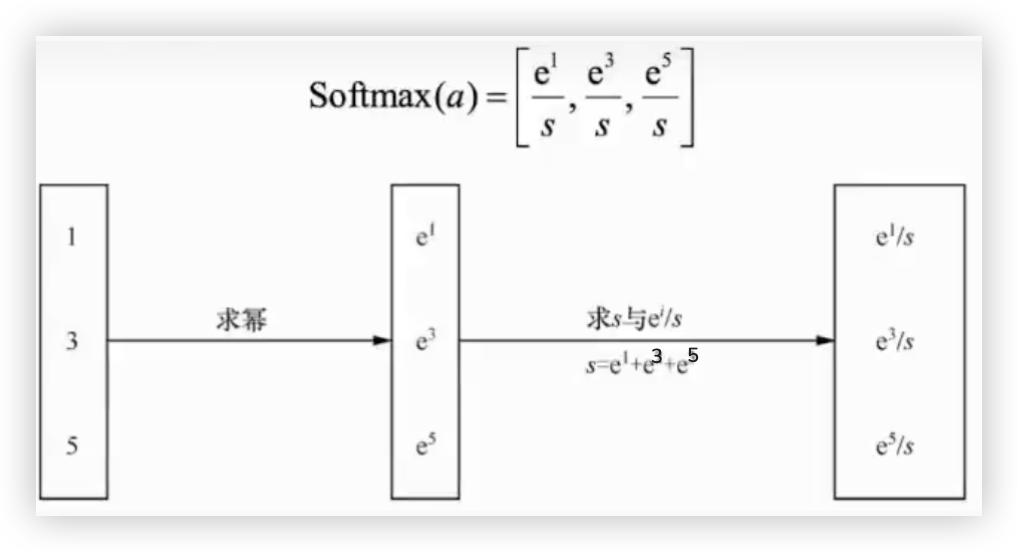
import numpy as np
def softmax(array):
t = np.exp(array) # t = [e^1,e^3,e^5]
s = np.sum(t) # s = e^1 + e^3 + e^5
result = t / s
return result
a = np.array([1, 3, 5])
result = softmax(a)
print(result) # [0.01587624 0.11731043 0.86681333] -- 验证了特征1 0 < 每个元素 < 1
print(sum(result)) # 1.0 -- 验证了特征2 每个元素相加之和等于1
print(np.argmax(a),np.argmax(result)) # 3 3 -- 最大元素的下标都是3
4*(1/100000) # 4e-05 这个是科学计数法!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# one-hot encoding
当样本标签为离散值时(3类标签分别表示为0、1、1),可以使用另一种方式来表示. 这种方式叫作独热编码.
离散值的标签使用独热编码进行表示后, 每个标签都变为一个数组, 每个标签数组的长度与数据集中样本标签值的种类一致..
# Softmax多分类器工作原理
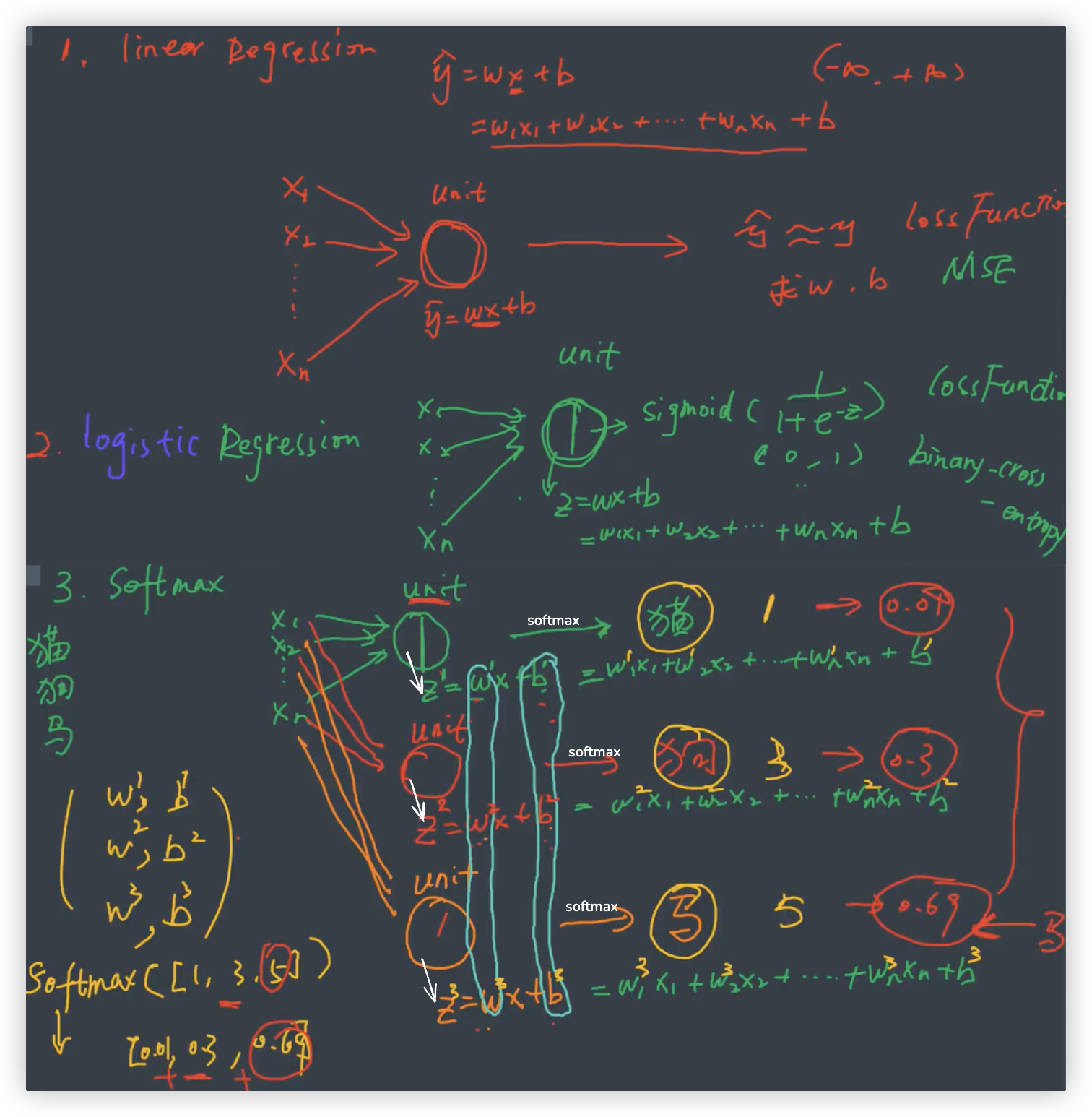
☆ 在这个截图中, softmax 有三组权重, 分别是关于 猫与非猫、狗与非狗、马与非马.. 的权重 (输入的都是同一个样本)
☆ 截图中, 逻辑回归的z是一个标量, softmax的z是根据unit的数量来决定,有多少个unit就有多少个z.
模型训练的目标: 让y_hat与y尽可能的接近, 通过lossfunction找的最优的w和b.
- 逻辑回归 = 线性回归+sigmoid.
与线性回归相比, 同样是输入一个样本, 但在线性回归的基础上通过sigmoid进行了一个映射再进行分段 连续值变成了离散值 - softmax可以简单理解成, 多分类拆解成了n个二分类
同样是一个样本输入, 但经过了 n个线性回归,得到的一组结果再进行softmax函数处理. （n等于类别数）
| loss function | w,b | 预测值 | |
|---|---|---|---|
| 线性回归 | MSE | 通过损失函数得到一组最优的w和b | 预测结果是一个值,范围 (-∞,+∞) |
| 逻辑回归-二分类 | 二元交叉熵 | 通过损失函数得到一组最优的w和b | 预测结果是一个值,它经过了sigmoid处理 值的范围 (0,1), 后续可通过0.5的阀值实现二分类 |
| softmax-多分类 | 多元交叉熵 | 输入同样一组特征,得到n组w和b | 预测结果是一组值(n个),它经过了softmax处理 |
ps: 上述softmax-多分类, 我们假设只有三个类别..那么n就等于3.
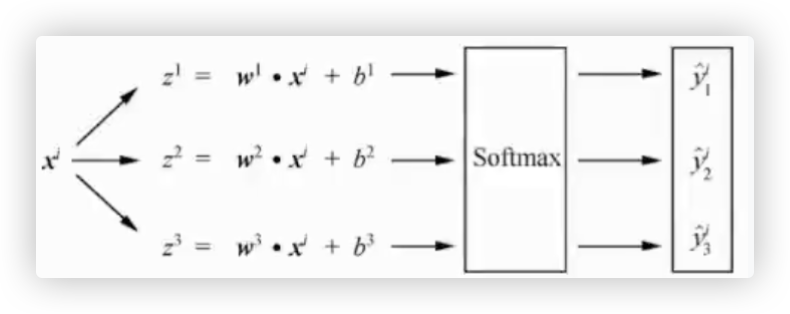
已知:模型是三类别 猫 狗 马,当前测试样本的真实类别是狗类别
- 模型经过训练后,得到了三组 w向量和b向量
- 将测试样本代入模型中,通过三个线性回归得到一组值[z1,z2,z3],这组值再通过softmax处理,得到一组结果[0.1,0.7, 0.2],
该组结果代表该样本分别属于猫 狗 马类别的概率为0.1、0.7、0.2
- 如何知道这个样本被预测为哪一类别呢？答案是, 预测值中最大值在数组中的位置即样本被预测的类别.
对于样本的预测值[0.1,0.7,0.2], 其中第2个值0.7为预测值中的最大值, 即预测该样本的类别为狗.
而且该样本的真实标签是狗,经过one-hot编码后结果为[0,1,0],
与 [0.1,0.7,0.2] 相比,不也就跟KL散度(描述两个概率分布)联系起来了吗!
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# 多元交叉熵
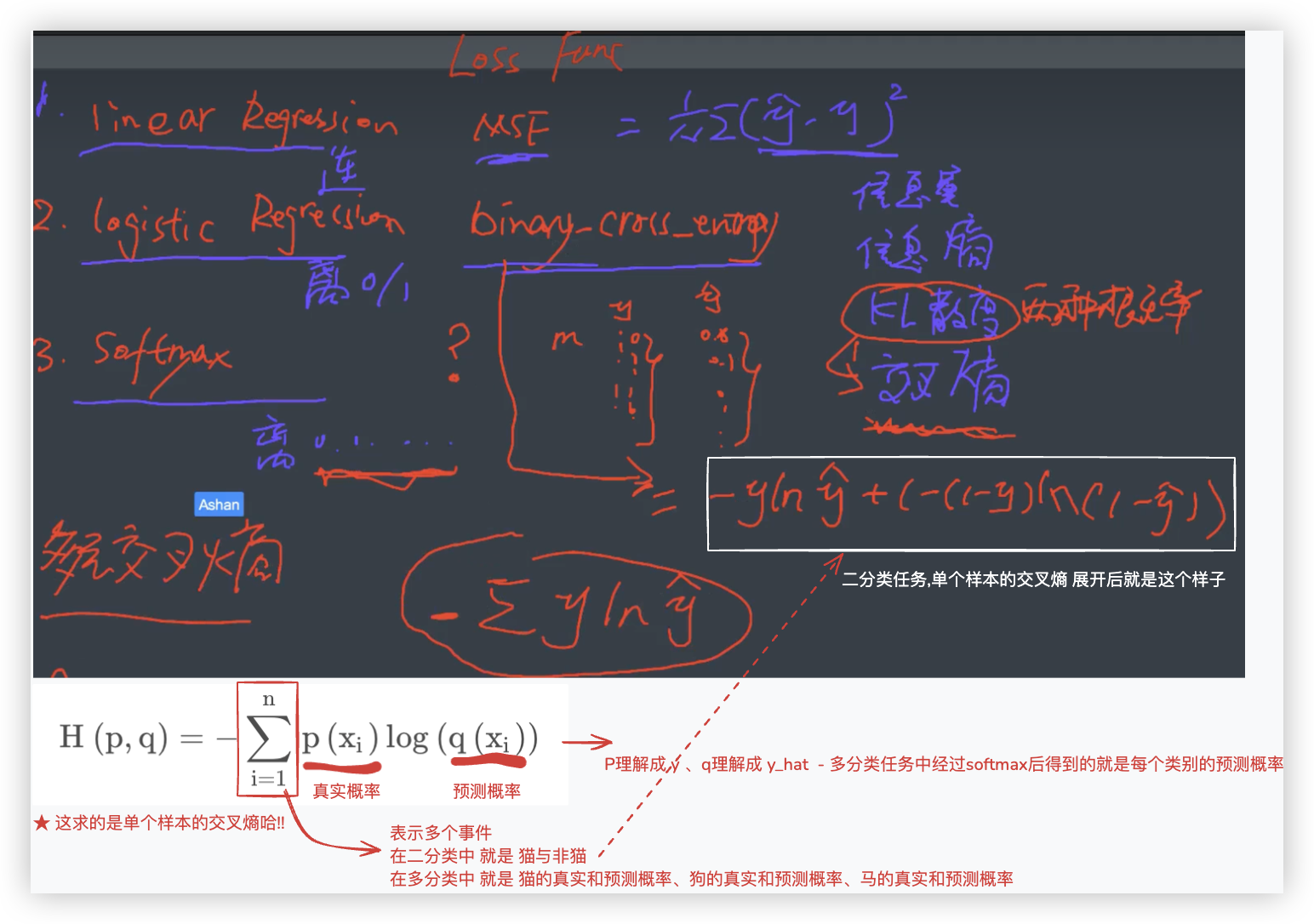
我们举个例子多分类任务的例子: (同样是一个样本,代入模型后,输出是一组值, 计算其损失)
我们用代码来实现 多元交叉熵:
def categorical_cross_entropy(y, y_hat):
"""
使用交叉熵计算样本标签值与预测值的差距
: y 某个样本的真实标签经过one-hot编码后的值
: y_hat 通过softmax模型预测后得到的一组值(预测的该样本的每个类别的概率值)
"""
n_classes = len(y)
loss = 0
for i in range(n_classes):
loss += - y[i] * np.log(y_hat[i])
return loss
y = [0, 1, 0]
y_hat = [0.2, 0.7, 0.1]
loss = categorical_cross_entropy(y, y_hat)
loss # 0.35667494393873245
y = [0, 1, 0]
y_hat = [0.2, 0.6, 0.2]
loss = categorical_cross_entropy(y, y_hat)
loss # 0.5108256237659907
y = [0, 1, 0]
y_hat = [0.3, 0.5, 0.2]
loss = categorical_cross_entropy(y, y_hat)
loss # 0.6931471805599453
y = [0, 1, 0]
y_hat = [0.6, 0.2, 0.2]
loss = categorical_cross_entropy(y, y_hat)
loss # 1.6094379124341003
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
你可以看到, 前三个y_hat都预测正确了, 但这三个y_hat与y之间的差异是不一样的.. 示例中,loss在增大..
最后一个y_hat预测错误了,它的loss相较于前面的,最大..
# 数据预处理
# 归一化
在线性回归的实战代码中用到了标准化, 那啥时候归一化,啥时候标准化呢? 哈哈哈, 自行查阅.
import numpy as np
X = [[-1, 2],
[-0.5, 6],
[0, 10],
[1, 18]]
X = np.array(X)
X_min = X.min(axis=0)
X_max = X.max(axis=0)
# X.shape,X_min.shape,X_max.shape >> (4, 2) (2,) (2,)
# 所以这里自动用到了广播机制 X_min本来只有一行,自己复制了三行,变成了4行2列
X_normalized = (X - X_min) / (X_max - X_min)
X_normalized
"""
array([[0. , 0. ],
[0.25, 0.25],
[0.5 , 0.5 ],
[1. , 1. ]])
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
还可以调用库来实现
from sklearn.preprocessing import MinMaxScaler
# 根据归一化的公式不难推算出
# 分子 0 <= x-x_min <= x_max-x_min ; 所以 0<= 归一化后每个元素 <= 1
# MinMaxScaler的feature_range可以指定 归一化后的每一个元素 处于哪个范围之间!!
sc = MinMaxScaler(feature_range=(0, 1))
X_normalized = sc.fit_transform(X)
X_normalized
"""
array([[0. , 0. ],
[0.25, 0.25],
[0.5 , 0.5 ],
[1. , 1. ]])
"""
# 相当于归一化后,反转,得到归一化之前的数组
X_restored = sc.inverse_transform(X_normalized)
print(X == X_restored)
"""
[[ True True]
[ True True]
[ True True]
[ True True]]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 扁平化
import numpy as np
image = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
image = np.array(image)
# 使用numpy中的reshape函数对图片进行扁平化操作
image = image.reshape((1, 9))
# 打印出经过扁平化操作的图片
print(image) # [[1 2 3 4 5 6 7 8 9]]
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# MNIST手写识别
MNIST手写识别数据集中有好几万张 28x28 的灰度图片. 每个像素点的值的范围处于 0-255 之间.
每个数字的图片都有很多张. 这是为了方便模型学习到 每个手写数字(0-10)各自的主要、关键特征..
# 数据加载与预处理
import numpy as np
from keras.datasets import mnist
# 加载MNIST数据集
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 定义独热编码函数
def one_hot_encoding(labels, n_classes):
result = np.eye(n_classes)[labels]
return result
# n_train与n_test分别表示训练集与测试集样本个数
n_train = X_train.shape[0] # 60000
n_test = X_test.shape[0] # 10000
# n_classes表示MNIST数据集的标签种类
n_classes = 10
# flatten_size为图片的像素总数,即扁平化后图片数组的长度
flatten_size = 28 * 28
# 将训练集图片进行归一化: 将图片中的每一个像素值转变为0~1之间
X_train = X_train / 255
# 对图片（特征）进行扁平化处理
X_train = X_train.reshape((n_train, flatten_size))
# 对标签进行独热编码
y_train = one_hot_encoding(y_train, n_classes)
#对测试集数据进行同样的操作
X_test = X_test / 255
X_test = X_test.reshape((n_test, flatten_size))
y_test = one_hot_encoding(y_test, n_classes)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 构建Softmax分类器模型
# 初始化模型参数 > 10个类别、28x28的图片,即图片特征有784个 > so,10组w和b
W = np.random.rand(10, 784) # 10行784列 其初始值随机
b = np.zeros((10, 1)) # 10行1列 其初始值为0
# 构建Softmax多分类器模型
def model(X):
"""
X是特征矩阵,其类型是 numpy.ndarray
以训练集为例,这里的X的形状是 (60000,784) 那么X.T转置后的形状就是 (784,60000)
"""
n_samples = X.shape[0]
# 这里是矩阵点乘 (10, 784)点乘(784,60000) W每一行与X.T的每一列对应元素相乘后再相加 > so,点乘后的形状 (10,60000)
# >> 每个分类器的W矩阵与每个样本数据进行点乘
# >> 像这样的式子有10个,每个式子的X是相同的,每个式子的wb不一样 w_1*x_1 + w_2*x_2 + .. + w_784*x_784 + b
# >> 点乘后的形状 (10,60000) 行是分类器,列是60000个样本,每个值是 样本在对应分类器上预测的概率!!
# 那么一列就是 一个样本在10个分类器上的预测概率
Z = W.dot(X.T) + b
# 接下来进行softmax
exp_Z = np.exp(Z) # 每个元素都取e为底的幂
sum_E = np.sum(exp_Z, axis=0)
y_hat = exp_Z / sum_E # exp_Z的形状(10, 60000) sum_E的形状(60000,)就1行60000个元素
"""
import numpy as np
a = np.array([[1,2],[3,4],[5,6]])
b = np.array([2,1])
print(a.shape,b.shape) # (3, 2) (2,)
print(a/b)
'''
array([[0.5, 2. ],
[1.5, 4. ],
[2.5, 6. ]])
'''
"""
return y_hat.T
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Softmax模型的训练
# 指定模型的次数与学习率
epochs = 20
lr = 0.05
# 使用[梯度下降算法]对模型进行训练
for epoch in range(epochs):
sum_w = np.zeros_like(W)
sum_b = np.zeros_like(b)
# 使用Softmax多分类器进行预测
y_hat = model(X_train)
# 计算模型参数的梯度值
# 多元交叉熵的梯度与二元交叉熵的梯度是一样的
# 计算的过程是用了矩阵的方式的来进行加速运算了的!!在代码里数据形状有点差异,需处理下,我就不深究了!
sum_w = np.dot((y_hat - y_train).T, X_train)
sum_b = np.sum((y_hat - y_train), axis=0).reshape(-1, 1)
grad_w = (1 / n_train) * sum_w
grad_b = (1 / n_train) * sum_b
# 使用梯度下降算法更新模型参数
W = W - lr * grad_w
b = b - lr * grad_b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 对模型进行评估
def get_accuarcy(X, y):
# 数据集中样本的个数
n_samples = X.shape[0]
y_hat = model(X)
# 使用Softmax多分类器预测的样本类别
y_hat = np.argmax(y_hat, axis=1)
# 样本的实际类别（标签值）
y = np.argmax(y, axis=1)
count = 0
for i in range(len(y_hat)):
if(y[i] == y_hat[i]):
count += 1
accuracy = count / n_samples
return accuracy
train_accuracy = get_accuarcy(X_train, y_train)
test_accuracy = get_accuarcy(X_test, y_test)
train_accuracy,test_accuracy
"""
(0.87995, 0.8862)
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22