LowB三人组
# 排序
排序: 将一组"无序"的记录序列调整为"有序"的记录序列.
列表排序: 将无序列表变为有序列表.
输入 - 列表
输出 - 有序列表
升序和降序
内置排序函数: sort()
常见的排序算法:
冒泡排序 、 选择排序 、插入排序 ; 快速排序 、 堆排序 、 归并排序 ; 希尔排序 、 计数排序 、桶排序、 基数排序
lowB三人组的时间复杂度都为O(n^2),且都是原地排序.
# 冒泡排序
冒泡排序 (Bubble Sort)
列表每两个相邻的数, 如果前面比后面大, 则交换这两个数.
一趟排序完成后, 无序区(没有排好序的)减少一个数, 有序区(已经排好序的)增一个数.
周而复始, 重复对无序区的冒泡过程..def bubble_sort(li): for i in range(len(li) - 1): flag = False for j in range(len(li) - i - 1): if li[j] > li[j + 1]: # 大于'>'是升序;小于'<'是降序 li[j + 1], li[j] = li[j], li[j + 1] flag = True if not flag: return1
2
3
4
5
6
7
8
9
时间复杂度: O(n^2)
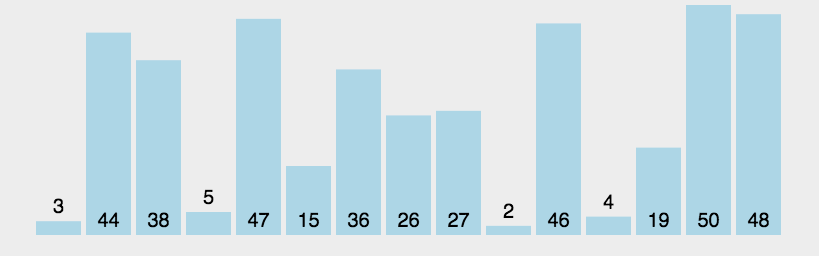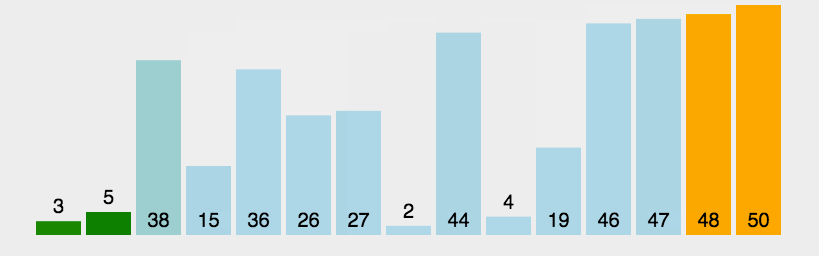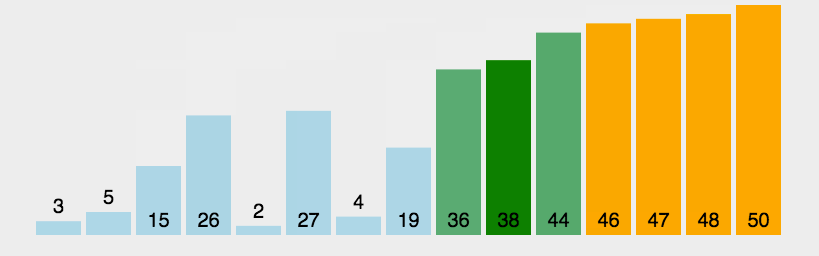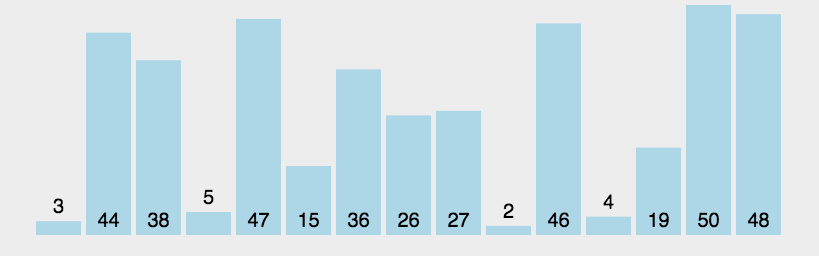
冒泡排序是原地排序, 不需要新的列表, 就在本来的列表上通过交换实现排序. 所谓的冒泡就是浮到顶端.
"""
假如列表有10个数,按理说需要冒泡10趟,但当无序区只有一个数时,就不用冒泡啦.So,共需要冒泡9趟.
range()函数从0开始,顾头不顾尾.. 从第0趟开始..到第8趟,共9趟.
所以要冒泡多少趟,等同于range(len(li)-1)
假如列表共10个数
第i趟 无序区数据数目len(li)-i 指针位置 是否交换会判断len(li)-i-1
0 10 0..-..8 -> range(9) 代表会判断9次
1 9 0..-..7 -> range(8)
... ... ...
7 3 0..-..1 -> range(2)
... ... ...
8 2 0 -> range(1)
★ 若一趟冒泡里没有发生任何交换,就可以该列表已经排好序啦!! -- 加一个标志位flag
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
代码实现
import random
def bubble_sort(li):
for i in range(len(li) - 1): # 第i趟.
flag = False
# 第i趟需要判断交换多少次
for j in range(len(li) - i - 1): # j是指针位置
if li[j] > li[j + 1]: # 判断交换 大于'>'是升序;小于'<'是降序
li[j + 1], li[j] = li[j], li[j + 1]
flag = True
if not flag:
return
li = [random.randint(0, 10) for i in range(10)]
print(li) # [3, 9, 10, 6, 9, 8, 3, 2, 5, 3]
bubble_sort(li)
print(li) # [2, 3, 3, 3, 5, 6, 8, 9, 9, 10]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 选择排序
选择排序 (select sort)
一趟排序记录最小的数, 放到第一个位置/无序区第一个位置;
再一趟排序记录列表无序区最小的数, 放到第二个位置/无序区第一个位置 ... 以此类推.
算法实现关键点: 无序区的范围、无序区最小数的位置.def sort_simple(li): for i in range(len(li) - 1): min_loc = i for j in range(i, len(li)): if li[j] < li[min_loc]: # 小于是升序;若是大于,则为降序 min_loc = j li[i], li[min_loc] = li[min_loc], li[i] return li1
2
3
4
5
6
7
8
时间复杂度: O(n^2)
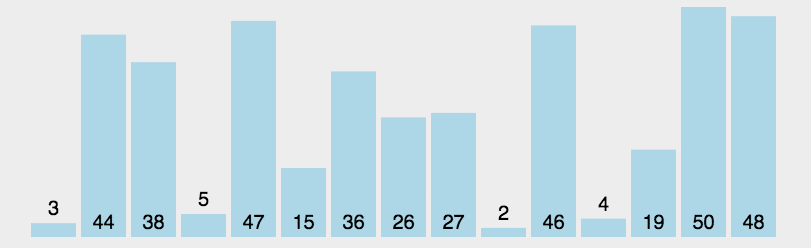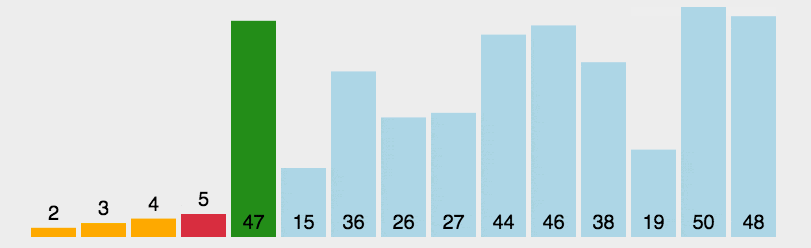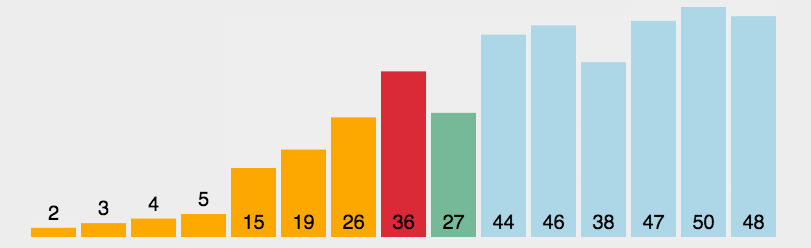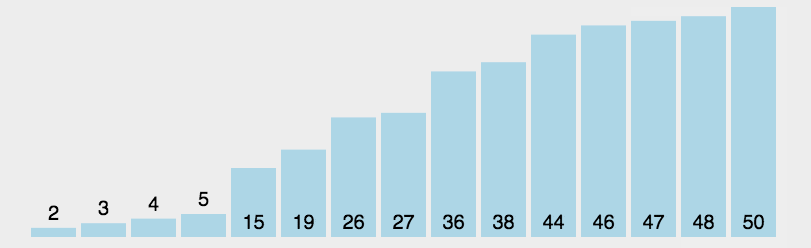
# 残缺版
时间复杂度 O(n^2); 用了两列表,浪费内存..
import random
def select_sort_simple(li):
li_new = []
for _ in range(len(li)): # 0(n)
min_val = min(li) # O(n)
li_new.append(min_val)
li.remove(min_val) # O(n) 遍历,找到第一个符合条件的元素删除,后面的元素往前移
return li_new
li = [random.randint(0, 20) for _ in range(10)]
print(li)
print(select_sort_simple(li))
"""
[19, 1, 14, 17, 3, 9, 17, 7, 5, 14]
[1, 3, 5, 7, 9, 14, 14, 17, 17, 19]
"""
# 注:不应该在for循环中修改被迭代的对象..
# for val in li:li.remove(val) -> 遍历li,val的值是li[0]、li[1]..这样来的.li在发生变化.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 完美版
不想开辟新的列表,但想把从无序区选出来最小的数放到某个地方.. 某个地方? 与无序区的 第一个位置/最后一个位置 进行交换.
这里我们以 放到无序区第一个位置 为例.
无序区的范围 -> 第0趟 0到最后;第1趟 1到最后;...;第i趟 i到最后.
import random
def sort_simple(li):
for i in range(len(li) - 1): # 与冒泡一样,第i趟
min_loc = i # 初始化 将无序区的第0个位置/最左边的位置 设置为无序区最小元素的位置
# 该for循环完毕后,min_loc就是无序区最小的那个元素的下标
# 优化:可以range(i+1, len(li)) 偷了一次懒.
for j in range(i, len(li)): # 遍历无序区,j是无序区元素的下标
if li[j] < li[min_loc]: # 小于是升序;若是大于,则为降序
min_loc = j
# 将无序区最小的那个元素与无序区最左边的元素进行交换
li[i], li[min_loc] = li[min_loc], li[i]
return li
li = [random.randint(0, 20) for _ in range(10)]
print(li)
print(sort_simple(li))
"""
[5, 5, 11, 8, 6, 0, 9, 3, 18, 6]
[0, 3, 5, 5, 6, 6, 8, 9, 11, 18]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
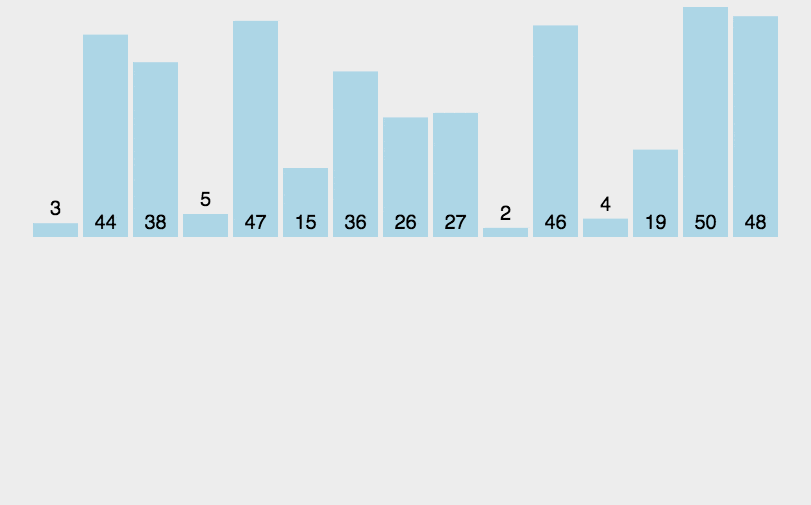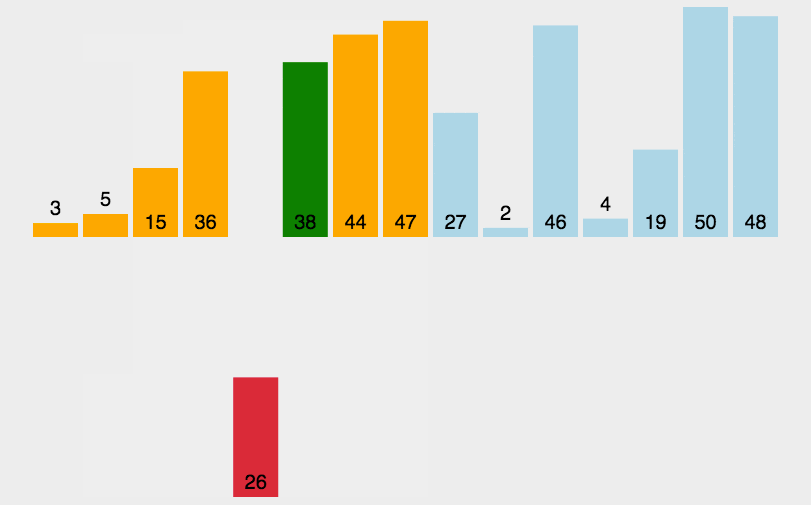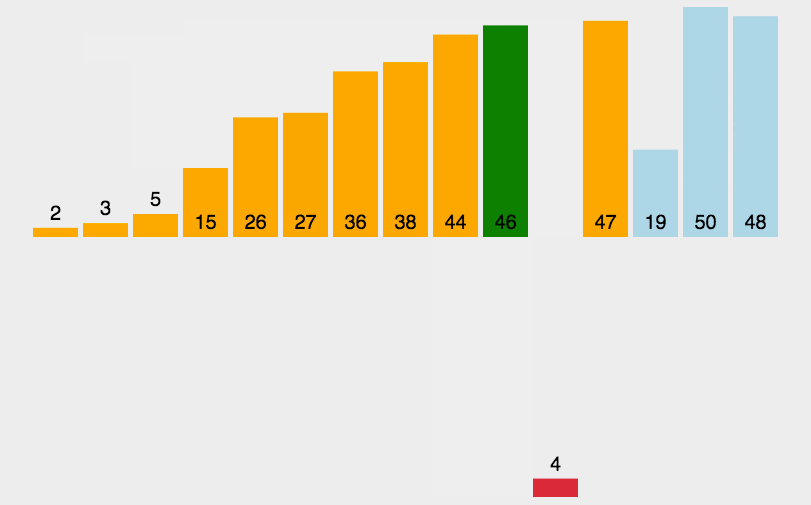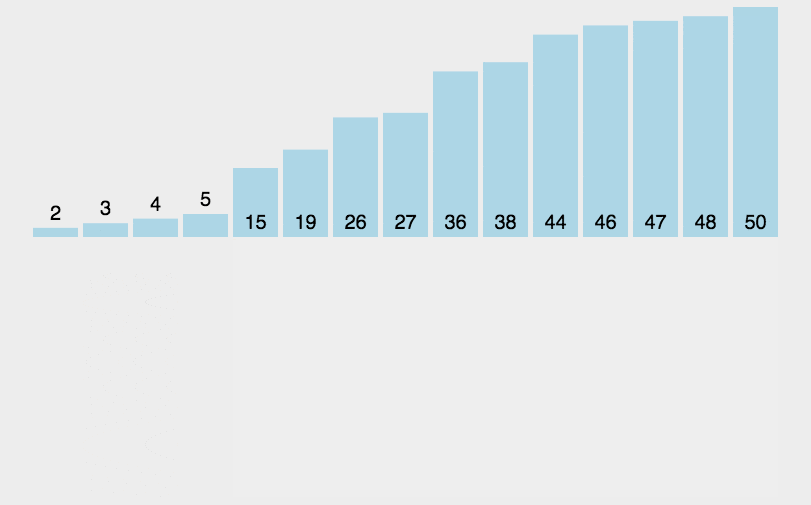
# 插入排序
类似于打牌.
初始的时, 手里(有序区)只有一张牌 ; 每次(从无序区)摸一张牌,插入到手里已有牌的正确位置.简单来说,就是:
比较后,若符合条件,会依次将有序区里的排往后挪动,直到条件不成立,此时将摸到的牌插入有序区挪动后空出的那个位置.def insert_sort(li): for i in range(1, len(li)): j = i - 1 temp = li[i] while j >= 0 and li[j] > temp: # li[j] > temp大于升序;若是小于,降序 li[j + 1] = li[j] j -= 1 li[j + 1] = temp return li # while循环可改成for循环??是可以的.可以借鉴后面桶排序那,保持每个桶是有序的,用的就是插入.1
2
3
4
5
6
7
8
9
10
11
时间复杂度: O(n^2)
"""
注:j下标位置的牌必定是手里的牌.
4 5 7 6 --> 一般情况
4 5 7 是手里的牌 ; 6 是摸到的牌
j = 2
7 < 6 , 7往右移动一个位置,直接覆盖掉6位置的数,摸到的牌会提前存储起来
现在就是 4 5 "空" 7
j = j -1 = 1
5 < 6 , 5原地不动..
6 这张摸到的牌 插入到 "空" 的位置, 即 j+1 的位置, 插入成功.
4 5 6 7 3 --> 极端情况
4 5 6 7 是手里的牌 ; 3 是摸到的牌
同理,7 6 5 4 都比3大, 会依次往右移动一个位置.
现在就是 "空" 4 5 6 7, 此时 j = -1
3 这张摸到的牌 插入到 "空" 的位置, 即 j+1=-1+1=0 的位置, 插入成功.
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
代码实现
import random
def insert_sort(li):
# 从下标1开始,是因为初始的时候,手里有一张下标为0的牌
for i in range(1, len(li)): # i表示摸到的牌的下标
j = i - 1 # j指的是手里的最后一张牌的下标
# 实现升序排,若手中的牌要比摸到的牌大,手中的牌要往后挪,会覆盖掉摸到的牌,所以需要将摸到的牌的值存储起来
temp = li[i]
# while循环找插入的位置
while j >= 0 and li[j] > temp: # 大于升序;若是小于,降序
# while循环开始时 li[j+1] 表明摸到牌; li[j] 表明手里最后一张牌
# 若手里最后一张牌li[j]大于摸到的牌li[j+1],将手中最后一张牌通过赋值的方式往后移动一个位置
# 不用担心,摸到的牌的值已经存储起来了
# 不断比较,极端情况就是:
# 当j=-1时表明 手中的牌都往 后/右 移动了一个位置
# 此时,只需要将摸到的牌插入到 第 j+1=-1+1=0 个位置.
li[j + 1] = li[j]
j -= 1 # j的箭头往左移动一个位置,便于继续比较手里的牌
li[j + 1] = temp # 插入摸到的牌
return li
li = [random.randint(0, 20) for _ in range(10)]
print(li) # [0, 14, 18, 19, 10, 6, 7, 15, 16, 17]
print(insert_sort(li)) # [0, 6, 7, 10, 14, 15, 16, 17, 18, 19]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26