全连接神经网络

FNN - 全连接神经网络
CNN - 图像处理
RNN - 序列处理 NPL

全连接神经网络 - 每一个unit都对后面一层的unit由所贡献! unit指的是神经元.
输入层（input layer）
输出层（output layer）
隐藏层（hidder layer）若网络结构中间的那些层,有很多个隐藏层,且形成一定的"深度",神经网络便称作深度学习!!

由输入层接收数据,隐藏层依次处理,最后由输出层进行输出的过程(这样一个数据流向的过程)称为正向传播(forward propagate)

1
2
3
4
5
6
7
8
9
10

# 全连接神经网络

★ 敲黑板: 在线性回归和逻辑回归二分类中, 只需一个unit, w是一个向量 [w_1,w_2,...,w_n];
在softmax多分类和全连接神经网络中, 因为有多个unit, 所以w是一个矩阵..

# 加权求和

在深度学习中,通常使用矩阵的形式来表示某一层中涉及的运算..

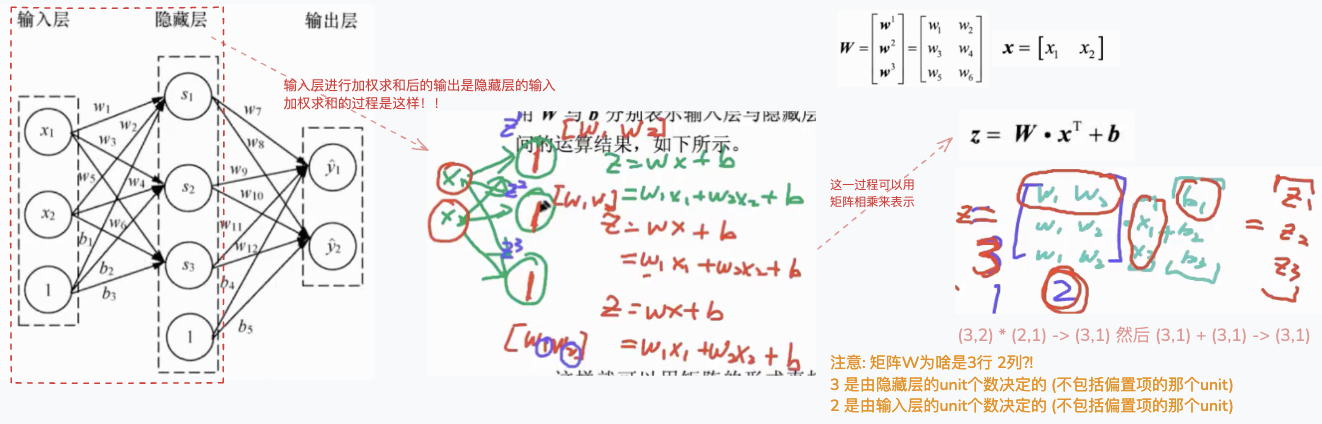
★ 务必与上篇博客中 Softmax多分类器工作原理小节的那个总结图结合起来理解..
关于上图中加权求和的过程.. 就像是 3个线性回归, 或者是softmax的前半部分,即输出多个z的过程.

# 激活函数

在隐藏层的3个单元s1、s2、s3分别接收到输入值z1、z2、z3后, 需要使用激活函数对接收到的输入值进行处理..

- loss function 的基本性质:
  它描述了y_hat与y之间的差异,两者相差越多,loss应越大;两者相差越小,loss应该越小
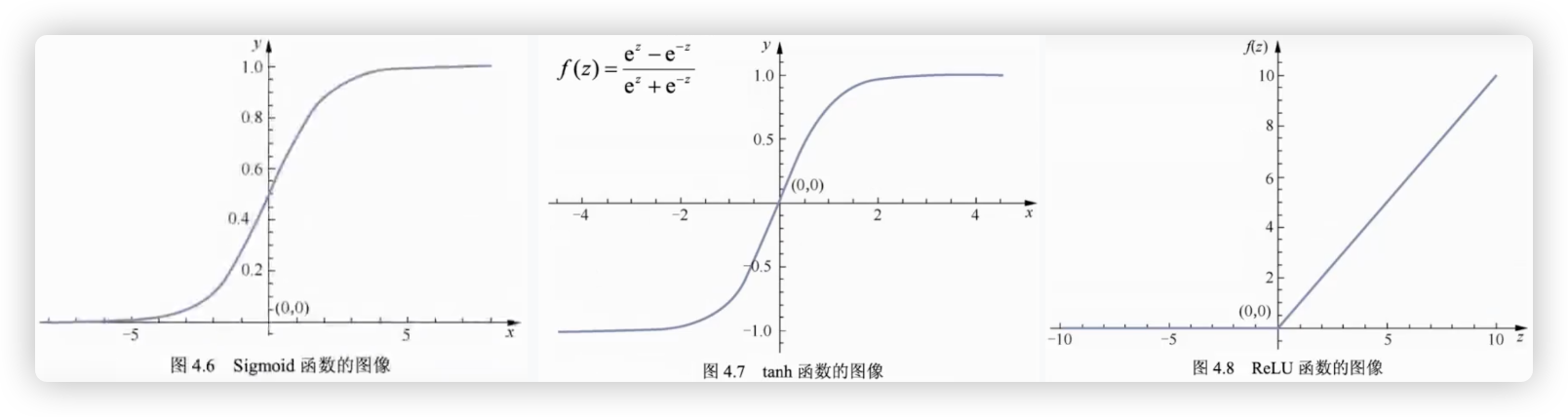
- activation function
  - sigmoid函数  输入一个值,将值的范围从（-∞,+∞）映射到 (0,1)
  - softmax函数  输入一组值,将组中每个元素的范围从（-∞,+∞）映射到 (0,1)
  - tanh函数     输入一个值,将值的范围从（-∞,+∞）映射到 (-1,1)
  - ReLU函数     分段函数,值小于于0,则等于0;值大于0,则值等于本身!!

1
2
3
4
5
6
7

用代码简单实现下.

# tanh函数 - 它是个奇函数哦,即tanh(-z)=-tanh(z)
import numpy as np
def tanh(z):
    y = (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z))
    return y

print(tanh(0))   # 0.0
print(tanh(1))   # 0.7615941559557649
print(tanh(-1))  # -0.7615941559557649


# ReLU函数
def ReLU(z):
    if z <= 0.0:
        return 0
    else:
        return z
print(ReLU(-10))  # 0
print(ReLU(8))    # 8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

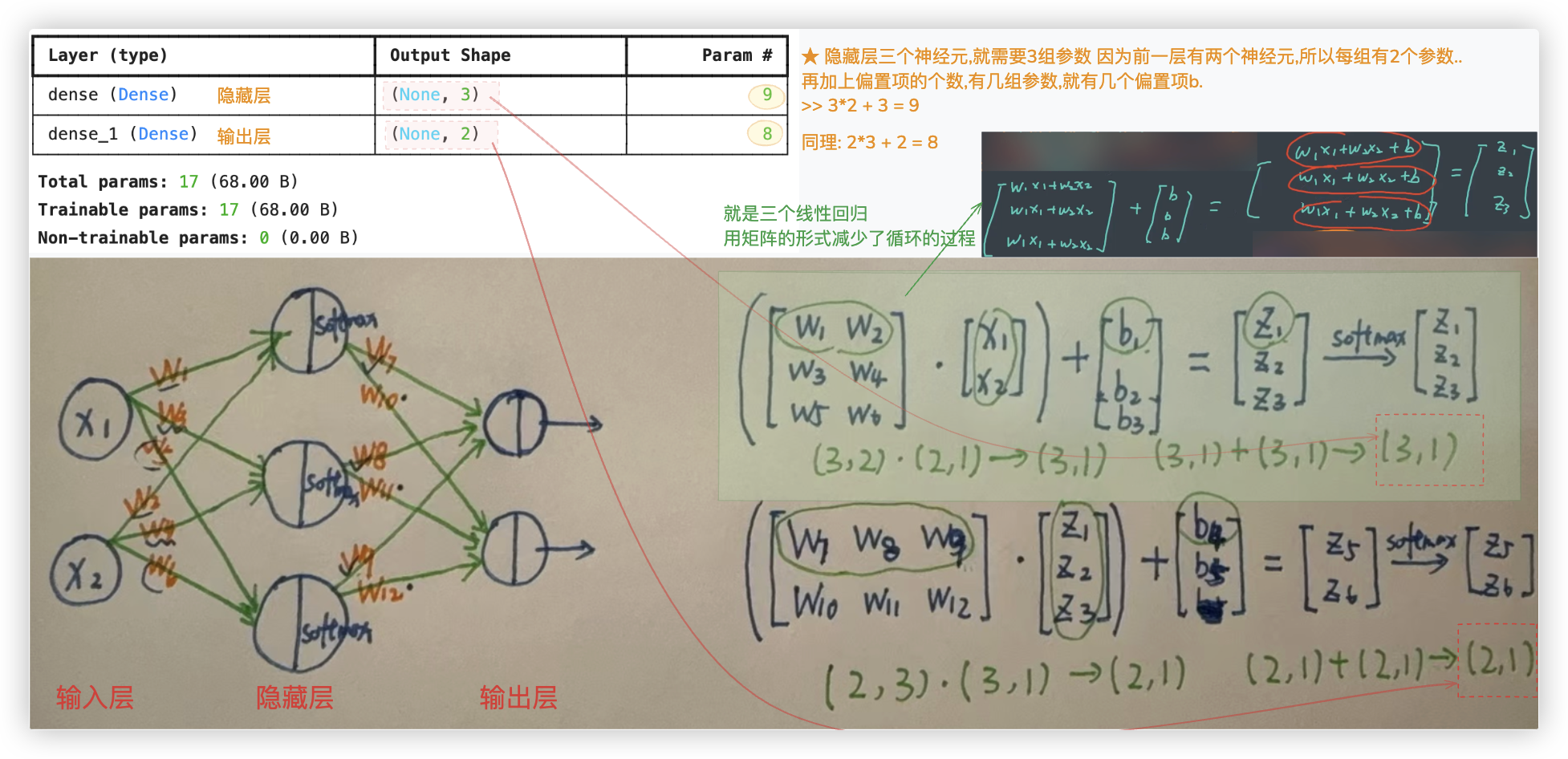
# 网络架构代码实现

用代码来实现下全连接神经网络的整体过程:

from keras.models import Sequential  # Sequential是序列的意思,意味着全连接神经网络从左到右是依次的
from keras.layers import Dense       # Dense密集的,指的就是全连接

# 初始化序列模型
model = Sequential()
# 在序列模型中加入隐藏层 添加的第一个层需一并指定输入层单元的个数
model.add(Dense(units=3,                    # 隐藏层神经元个数
                input_shape=(2,),           # 输入层的神经元个数
                activation='sigmoid',       # 隐藏层的激活函数
                kernel_initializer='ones',  # 隐藏层初始的w的值都为1
                bias_initializer='zeros'))  # 隐藏层初始的b的值都为0
# 在序列模型中加入输出层
model.add(Dense(units=2,                    # 输出层神经元个数
                activation='softmax',       # 输出层的激活函数
                kernel_initializer='ones',  # 输出层初始的w的值都为1
                bias_initializer='zeros'))  # 输出层初始的b的值都为0

model.summary()  # 查看模型

"""
补充: 
  关于模型参数初始化,我们一般不会像该示例中一样初始化为常数.
  随机初始化模型参数,可指定随机生成的参数服从正态分布、均匀分布等概率分布. 注:W是一个矩阵
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

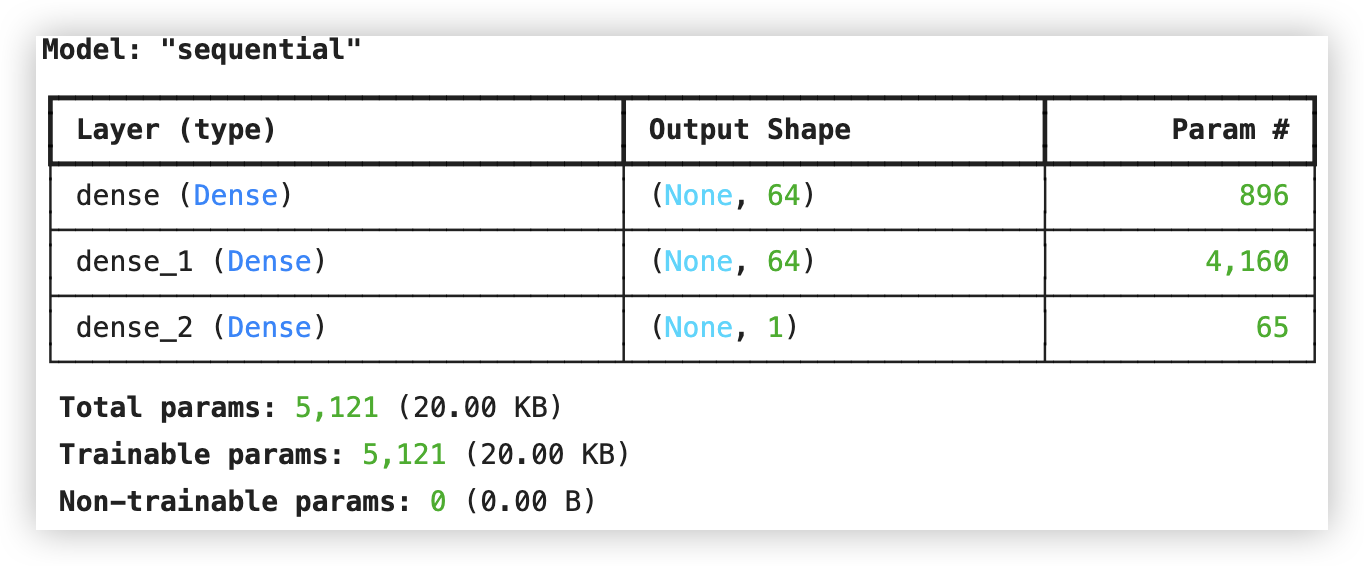
除输入层外,该模型有两个全连接层,分别默认命名为 dense和dense_1..
Total params 总共参数; Trainable params 可训练的参数.

# 梯度下降算法

神经网络中依旧使用的是梯度下降算法..
在该小节, 我们将依次探究下面三个问题:

■ 反向传播算法
在前3章中,都采用梯度下降算法来计算、更新模型的参数.在使用梯度下降算法之前,必须得到损失函数关于参数的梯度值.
- 在传统机器学习中,模型的参数一般较少,所以可以使用推导的方式来求梯度值.
- 但是对于深度学习模型,因模型的参数很多 <在神经网络中,有很多层,每层都有很多unit.>
  所以就需要使用一种新的算法即反向传播（back propagation）算法来求损失函数关于所有参数的梯度值
  
■ 3种梯度下降算法的计算方式
在前3章中介绍的机器学习模型时. 每一次都根据训练集的全部数据计算损失值,然后求解参数的梯度值,最后利用梯度下降算法更新参数.
当训练集中的数据量较大时,这种方式会变得非常没有效率.
如果每次计算损失值时只使用小部分训练集数据,或者只使用一个训练集的样本,会让模型训练更有效率.

■ 梯度下降优化算法
除此之外,因为深度学习模型的参数特别多,普通的梯度下降算法很难很好地更新模型的参数.
所以需要对梯度下降算法进行优化,使其可以很好地更新复杂的深度学习模型.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 反向传播算法

神经网络模型参数太多, 手动推导求梯度不现实, 用反向传播算法来求梯度.

反向传播本质就是高数里的链式求导法则..

具体的过程,书上的看不大懂 (高数知识都忘完了), 可以看下深度学习-01.深度学习基础.md这篇博客中关于反向传播的阐述..

# 梯度下降算法计算方式

在计算损失函数关于模型参数的梯度值时,根据使用的训练集数据量,可以将梯度下降算法分为以下3种

关于这三个算法的详细介绍看书上内容. 简单来说, 就是参与梯度下降的样本数量不同.

- 批量梯度下降算法(batch gradient descent)      > 只使用训练集中全部样本数据
- 随机梯度下降算法(stochastic grasient descent) > 只使用训练集中一个样本
- 小批量梯度下降(mini-batch gradient descent)   > 批量和随机 的折中算法,比如使用 16个、32个或64个等

★ 则以MSE为例,公式最前面的 1/N, 这三个算法N的值分别为 N、1、16

1
2
3
4
5

# 梯度下降优化算法

会自动的调整学习率的值让模型更快更好的收敛

不用深究, 通常会选用下面5个梯度下降优化算法在代码里,就是优化器的选择..

SGD 就是随机梯度下降算法
Adagrad
Adadelta
RMSprop 
Adam

RMSprop、Adam 这两个用的最多!! 一般就选择Adam

1
2
3
4
5
6
7

# MNIST手写数字识别 - 分类

# 数据预处理

from keras.datasets import mnist
from keras.utils import to_categorical

(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 将训练集图片进行归一化: 将图片中的每一个像素值转变为0~1之间
X_train = X_train / 255.0 
X_test = X_test / 255.0
# 将 label转化为独热编码的形式
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

1
2
3
4
5
6
7
8
9
10

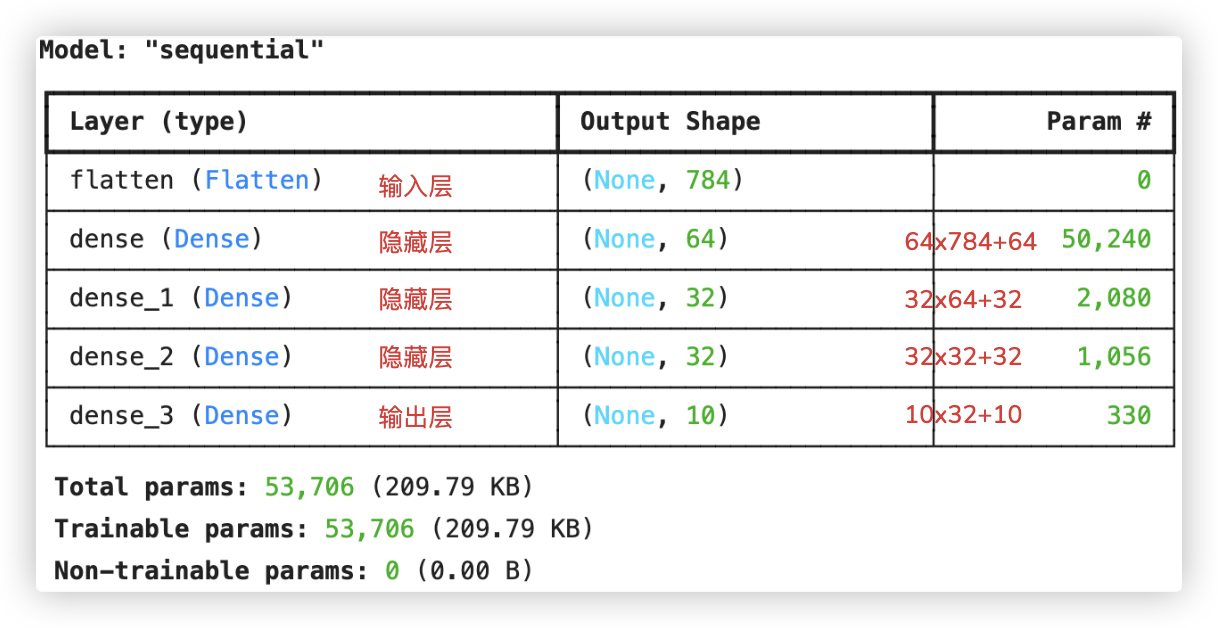
# 构建神经网络结构

from keras.models import Sequential
from keras.layers import Dense, Flatten

model = Sequential()
model.add(Flatten(input_shape=(28, 28)))       # 输入层,Flatten将28x28的图片展平,二维变一维
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=32, activation='relu'))
model.add(Dense(units=32, activation='relu'))
model.add(Dense(units=10, activation='softmax'))
model.summary()

1
2
3
4
5
6
7
8
9
10

# 模型编译

from keras.optimizers import RMSprop

model.compile(loss='categorical_crossentropy',   # 指定损失函数
              metrics=['accuracy'],              # 指定分类模型评估的方式 用准确率
              optimizer=RMSprop())               # 指定优化器,即模型训练时使用的梯度下降算法

1
2
3
4
5

# 模型训练

★ 准确点是使用所有训练集样本,分批次的进行模型训练~

model.fit(X_train, 
          y_train, 
          epochs=10,             # 10次迭代
          batch_size=64,         # 每次训练使用训练集中的64个样本（注:若用了数据增强,该参数的指定在数据增强那）
          validation_split=0.2)  # 将训练集中的20%的数据划分出来作为验证集

1
2
3
4
5

X_train 经过 validation_split=0.2 后, 剩余 48000 个样本用于训练. 48000/64=750
即10次迭代, 每批次64个样本, 则每个迭代中的BP次数等于 X_train的样本数除以64..

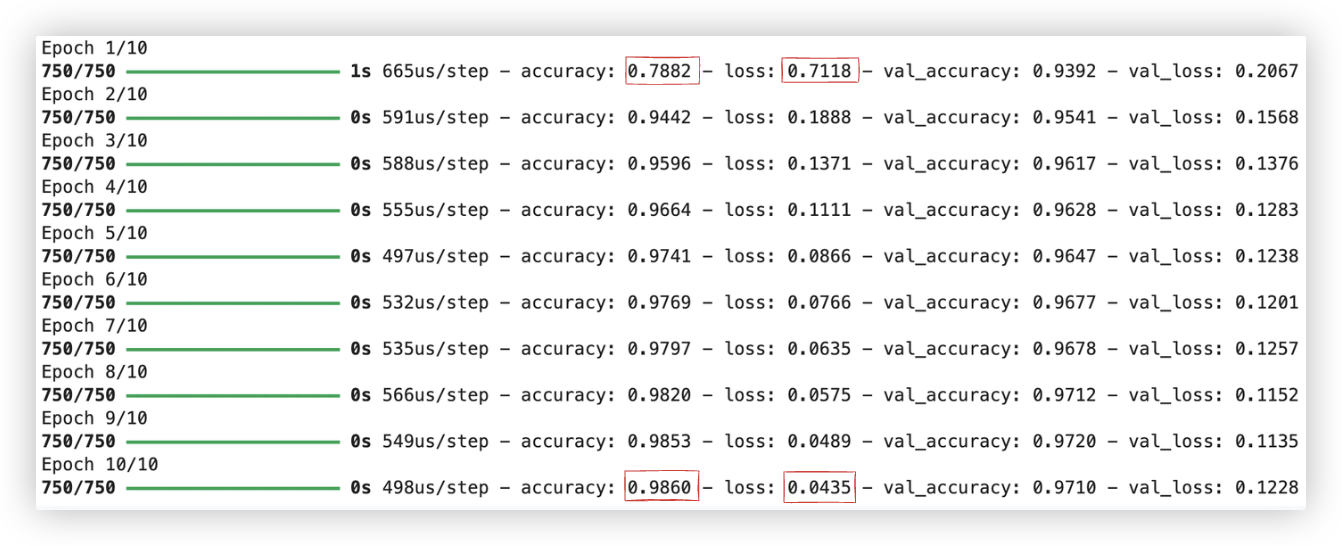
accuracy、loss是训练集每次迭代的损失和准确率; val_accuracy、val_loss是验证集每次迭代的损失和准确率..
看起来每次迭代训练集和验证集都相差不大, 效果也还不错, 就不用调整模型了.

# 测试集评估

loss, accuracy = model.evaluate(X_test, y_test)
print(accuracy)

"""
313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 236us/step - accuracy: 0.9673 - loss: 0.1252
0.9706000089645386
"""

1
2
3
4
5
6
7

# 房价数据分析 - 回归

没啥可注意的,都到差不差的.

from keras.datasets import boston_housing as bh
(X_train, y_train), (X_test, y_test) = bh.load_data()

# 求取训练集数据中每一个特征值的均值
mean = X_train.mean(axis=0)
# 求取训练集数据中每一个特征值的方差
std = X_train.std(axis=0)
# 对训练集与测试集进行标准化
X_train = (X_train - mean) / std
X_test = (X_test - mean) / std

print(X_train[0])
print(y_train[0])
"""
[-0.27224633 -0.48361547 -0.43576161 -0.25683275 -0.1652266  -0.1764426
  0.81306188  0.1166983  -0.62624905 -0.59517003  1.14850044  0.44807713
  0.8252202 ]
15.2
"""

from keras.models import Sequential
from keras.layers import Dense 
from keras.optimizers import Adam

model = Sequential()
model.add(Dense(64, input_shape=(13,), activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(1, activation=None))
model.summary()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

model.compile(optimizer=Adam(),
              loss='mse',
              metrics=['mae'])

model.fit(X_train, 
          y_train, 
          epochs=300, 
          batch_size=32, 
          validation_split=0.2)

_, loss = model.evaluate(X_test, y_test)
print(loss)

"""
4/4 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 16.8789 - mae: 2.5196
2.698709011077881
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

← softmax多分类器神经网络模型优化→