DC's blog
DC
2025-01-21
目录

逻辑回归

机器学习的 有监督学习 分为了 回归(regression)和分析(classification).
逻辑回归(logistic regression) 尽管英文直译中有回归两字, 但它是解决分类任务的. - 二分类.

image-20250122191553404

# 逻辑回归的数学表达式

逻辑回归 = sigmoid函数 + 线性回归

第一步: 先看看sigmoid函数的数学表达式.

image-20250122090153535 
import numpy as np
def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(-10, 10, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.scatter(0, sigmoid(0))
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
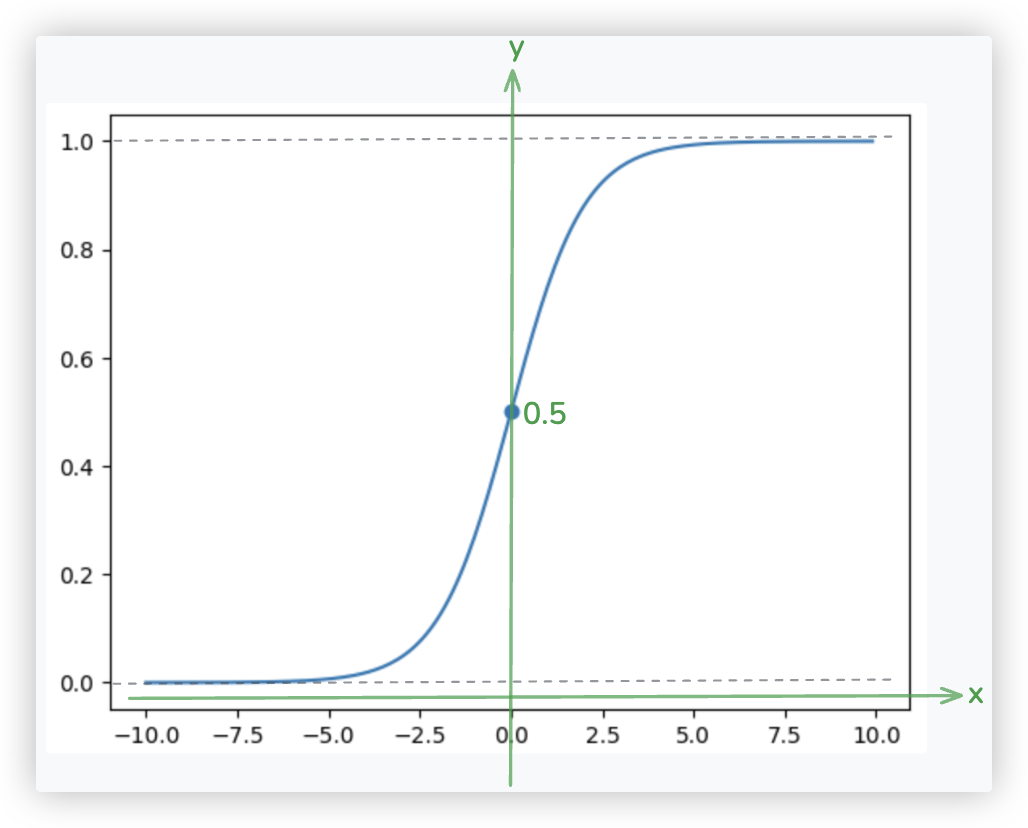
image-20250122085552839

第二步: 分析逻辑回归模型的函数的数学表达式.

image-20250122173333183 
1. linear regression
   x的取值范围(-∞,+∞) -->>-- 经过y = WX + b处理后 -->>-- y的取值范围(-∞,+∞)
2. logistic regression
   逻辑回归 = sigmoid函数 + 线性回归
   x的取值范围(-∞,+∞) -->>-- 经过y = WX + b处理后 -->>-- y的取值范围(-∞,+∞) 
   -->>-- 经过sigmoid函数 -->>-- y的取值范围(0,1) -->>-- 再设置阈值,进行分段处理!! 
   当y_hat预测值在大于0.5 y_hat=1;  eg 1类别猫
   当y_hat预测值在小于0.5 y_hat=0;  eg 0类别非猫
  
★ 抓住sigmoid函数的本质 - 就是将y_hat的值从实数范围映射到0-1的范围..
1
2
3
4
5
6
7
8
9
10

# 逻辑回归-损失函数 MSE?

No. 有两点:

  1. MSE作逻辑回归的损失函数,它是一个非凸函数,有多个最小值, 梯度下降在非凸中的作用有局限性.
  2. 从 损失函数应基本满足的性质出发, 分对的损失是0, 分错的损失是1.. 分错了,损失才只有1, 分错的惩罚力度太小了!
  • 我们先简单分析下, y=w+b 求解w,b 我们可以有无数组w,b,但我们要找到让y_hat尽可能接近y的那一组w,b (最优w,b).
    MSE lossfunction 描述了y_hat与y之间的差异!
  • 同样的,在逻辑回归中,我们也要求解最优的w和b,使loss最小..
  • 那么MSE能不能作为逻辑回归的损失函数?? 不能, 有两点原因..

# 第一点: 非凸函数

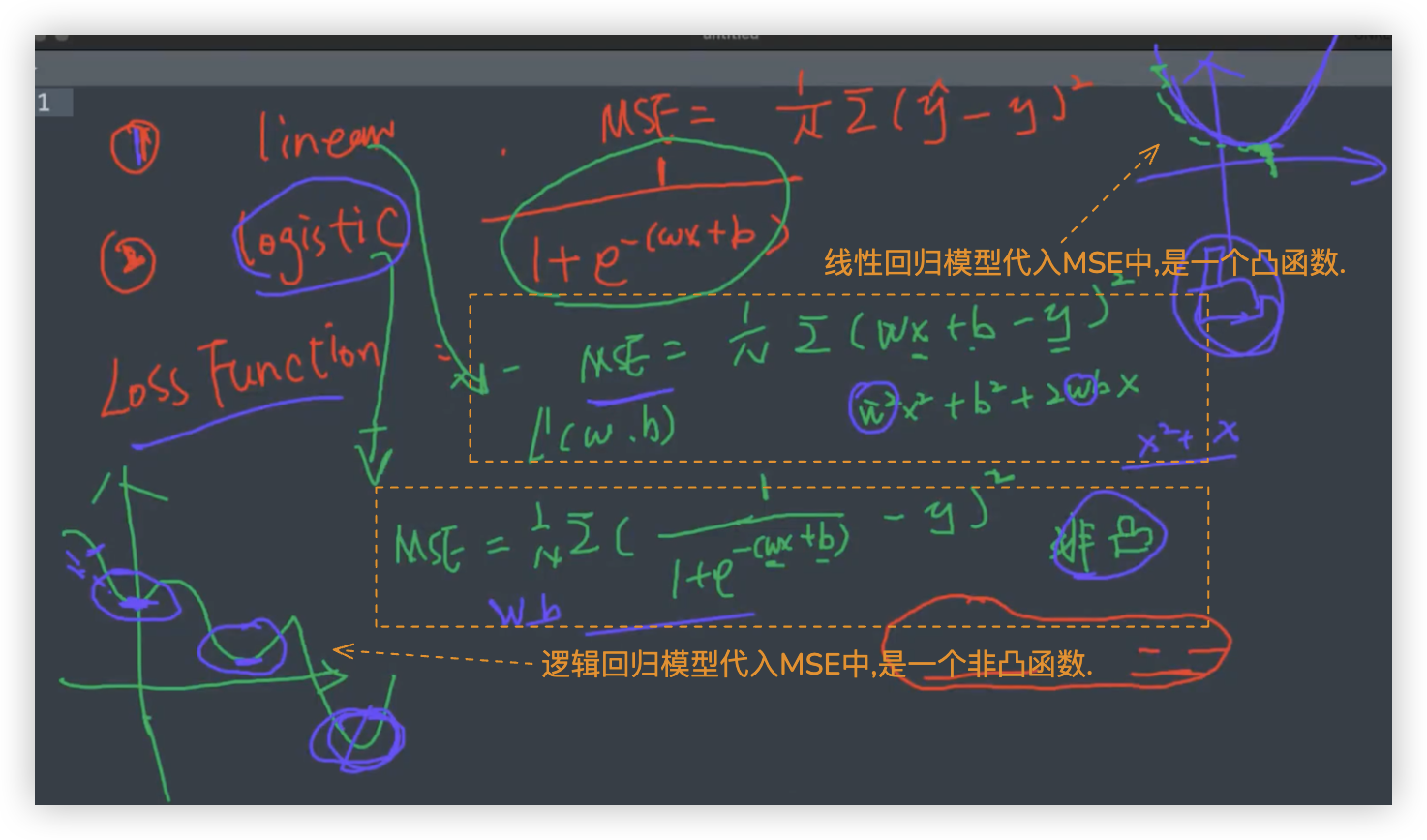
image-20250122100036677

将线性回归模型代入MSE中, 得到的是一个关于w和b的二次多项式, 二次多项式是一个凸函数, 具有最小值.
将逻辑回归模型代入MSE中, 是一个非凸函数. 具有局部最小值, 在梯度下降算法中, 可能会落入局部最小值,反复迭代而跳不出.

- 什么是凸函数呢?粗略了解下,凸函数有一个最小值! 
  梯度下降时,是随机w和b,通过不断迭代找到最小值.无论迭代多少次,只会收敛到最小值那.
- 若让MSE作为逻辑函数的损失函数,其损失函数图像是一个非凸函数! 
  非凸函数粗略理解就是有很多个最小值,用梯度下降算法只会收敛到第一个最小值那!!不管迭代多少次,最后只会在局部最小值那蹦跶.

也就是说
- 非凸函数可能有多个局部最小值或鞍点
- 梯度下降算法依赖初始点,不同的初始化可能导致最终收敛到不同的局部最小值
- 使用梯度下降时,可能会陷入局部最小值,或者停留在鞍点（梯度为零但并不是最小值）
所以,梯度下降算法并不是严格地只适用于凸函数,而是能在非凸优化中发挥作用,只是其效果和稳定性会受到非凸性质的限制!!
1
2
3
4
5
6
7
8
9
10

So. 不能用MSE作为逻辑回归的损失函数, 因为将模型代入损失函数后
应用梯度下降,根据图像的性质,是非凸函数,只能找到局部最小值, 而不是全局最小值..

# 第二点: 惩罚力度太小

从 损失函数应基本满足的性质出发 来解释为何MSE不能作逻辑回归的损失函数.

损失函数的基本性质:
- 当y_hat与y之间的差异越小,损失函数的值也越小
- 当y_hat与y之间的差异越大,损失函数的值也越大
1
2
3
image-20250122121054163

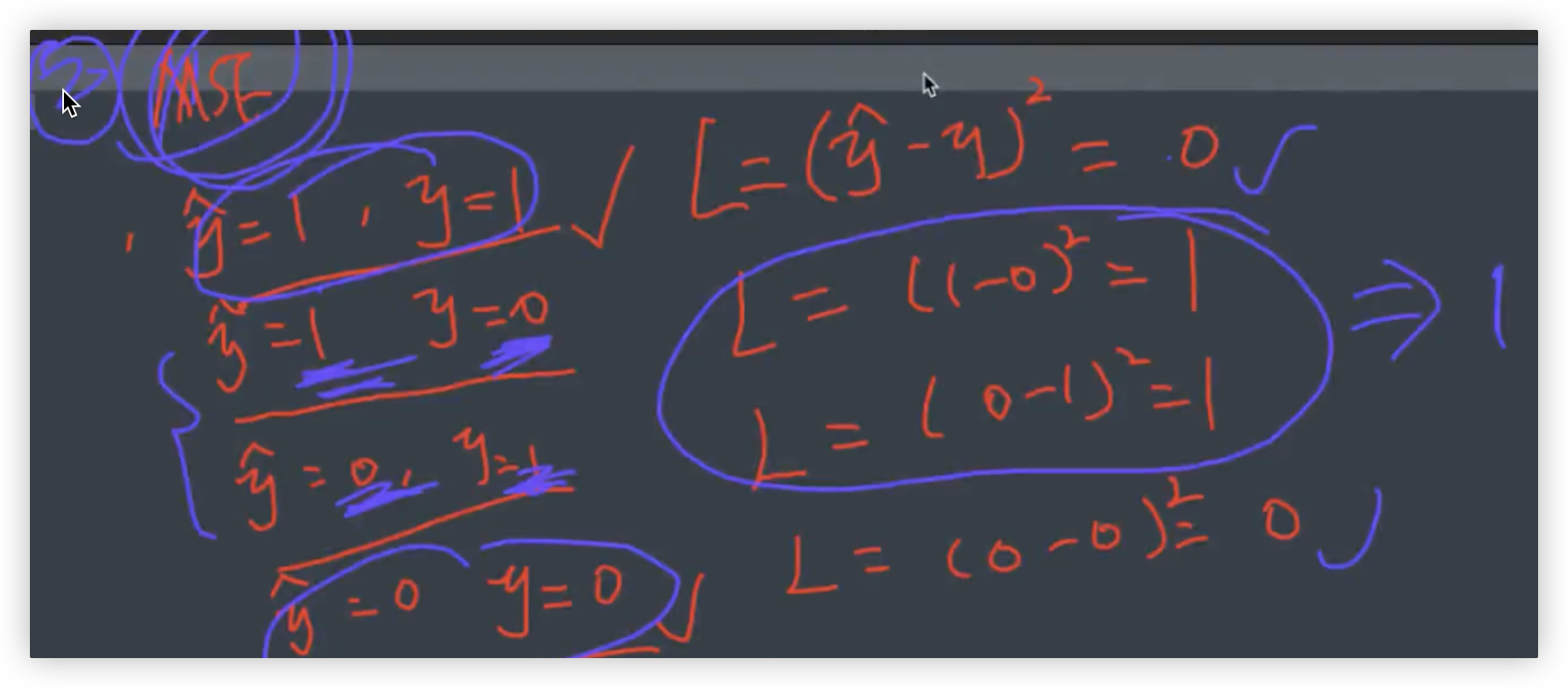
将类别0预测成1,将类别1预测成0, 预测错了, 损失才只有1, 分错的惩罚力度太小了呀..

# 信息论的基本知识

MSE不适合作为逻辑回归的损失函数, 那什么损失函数适合作为逻辑回归的损失函数呢?
先来了解一点信息论的知识.. 为后续二元交叉熵损失函数作铺垫..

# 信息量

image-20250122111019545 
信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”, 也就是说衡量信息量的大小就是看这个信息消除不确定性的程度.
- 太阳从东边升起 大家都知道,是确定的事情,这说的不就是废话嘛! 所以,这句话信息量为0.
- 从100个老师中抽中你; 从1000个老师中抽中你
  很显然,后者的不确定性比前者大,因为前者抽中你的概率为1/100,后者为1/1000
  
> 上述可总结如下: 信息量的大小与信息发生的概率成反比. 概率越大,信息量越小; 概率越小,信息量越大.
  公式表示 如上面的截图所示!! （负号就表示了反比）
1
2
3
4
5
6
7

# 信息熵 (熵)

信息熵也被称为熵, 用来表示所有信息量的期望. - 期望是试验中每次可能结果的概率乘以其结果的总和.
单看概念有点生涩, 结合公式和天气的示例就很容易理解了.

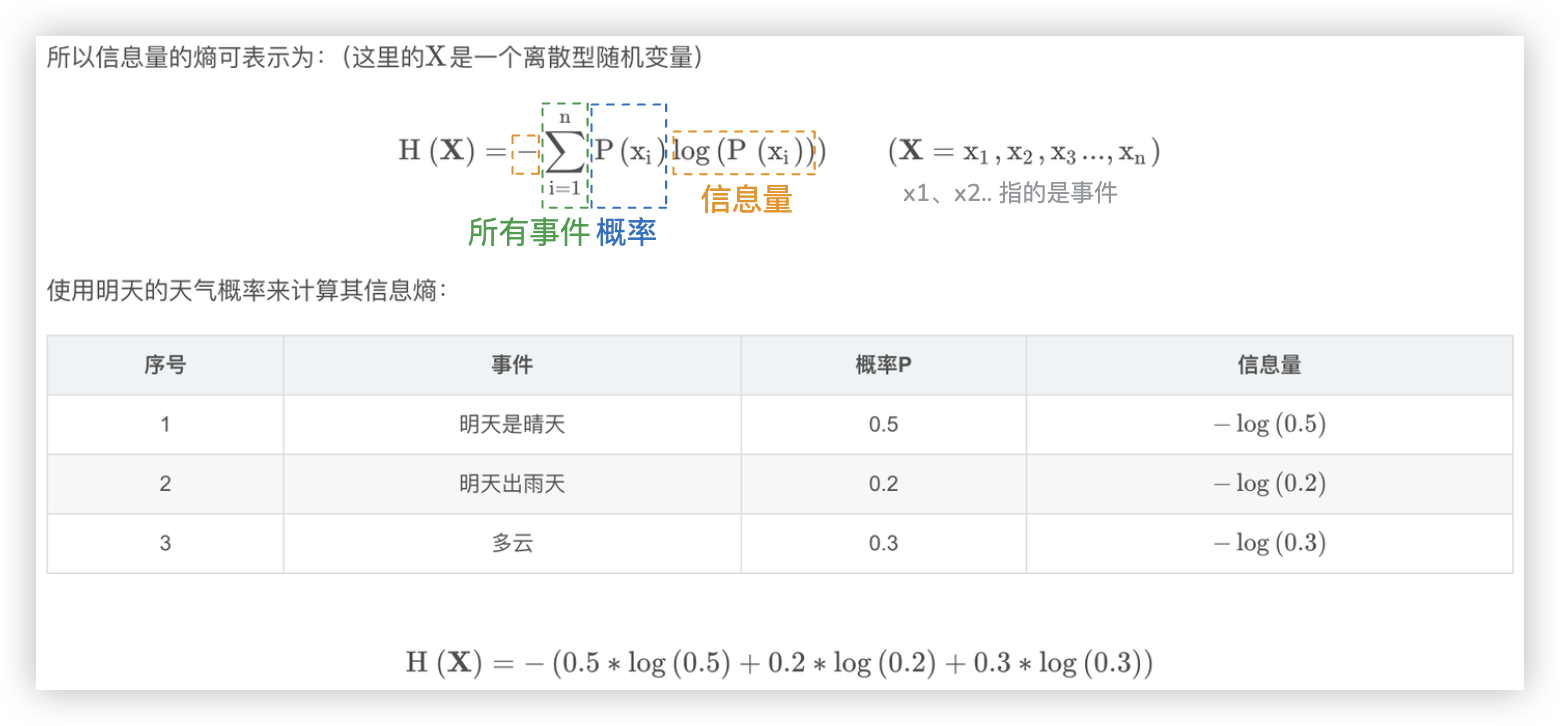
image-20250122115035285

Ps: 换成二分类的例子, 就是 [是猫的概率乘以是猫的信息量] 加上 [不是猫的概率乘以不是猫的信息量].
So, 对于0-1分布的问题, 计算熵的公式可以简化如下:

image-20250122141551622

细心的你会发现, 信息熵公式跟二元交叉熵的公式有点像了, 只不过信息熵中只有P, 二元交叉熵中是 P和Q.

# 相对熵 (KL散度)

先说结论: KL散度 = 交叉熵 - 信息熵

  • 假设有一个三分类任务, 标签类别为 猫,狗,马..
    • P往往用来表示样本的真实分布, 比如 [1,0,0] 表示当前样本属于第一类 猫.
    • Q往往用来表示模型所预测的分布, 比如[0.7,0.2,0.1] 表示当前样本是猫狗马的概率分别为 0.7, 0.2, 0.1
  • 我们可以使用 KL散度 来 表示P和Q这两个概率分布之间的差异
    • KL散度的值越小, 表示 P和Q这两个概率分布 越接近, 反之则越不接近.
    • 我们可以通过反复训练模型, 让Q的分布逼近P

KL散度的公式如下:

image-20250122163926240

上面求得了 当前样本分别是猫、狗、马时的散度, 然后相加.. ☆ 即得到了当前样本 y与y_hat之前的差异..

我们将KL散度公式拆开, 变下形 就可以得到 KL散度 = 交叉熵 - 信息熵

image-20250122164530195

再思考一个问题, 至此, 我们可以将KL散度作为 逻辑回归的损失函数..
但, p(x)是固定的标签y对应的概率, 是一个常量. 真正决定 KL散度 的是 交叉熵..
所以, 我们就用交叉熵 作为逻辑回归的损失函数.. 交叉熵里有P有Q,所以叫做交叉; i的取值 只有两个,代表两分类,所以通常用 二元交叉熵

# 损失函数-二元交叉熵

# 公式概念解析

image-20250122172011998

ps: ☆ KL散度公式中交叉熵部分,指的是单个样本的交叉熵..  
往下的L(w,b)指的是二分类任务中多个样本的平均交叉熵...
L(w,b)中单个样本的交叉熵的求和符号是没有的,是展开成了该样本类别0和类别1的交叉熵之和. 别懵逼了..

# 惩罚力度无穷大

Q: 为啥采用二元交叉熵作为逻辑回归的损失函数?

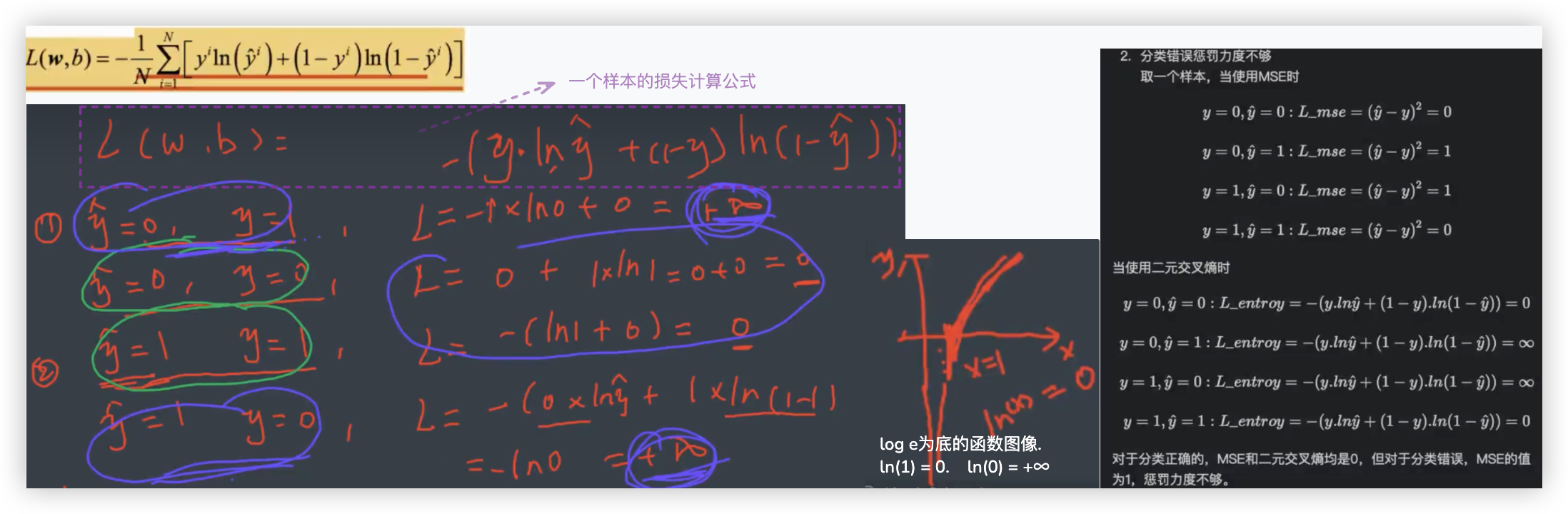
image-20250122123110104 
- 上面的截图我们使用的是一个样本作分析, 探究了二元交叉熵 是否满足 损失函数应基本满足的性质！
  - 当y_hat与y之间的差异越小,损失函数的值也越小
  - 当y_hat与y之间的差异越大,损å失函数的值也越大
  可以看到,经过剖析,是符合我们的预期的,分类错误了,损失就应该无限大!!分错的惩罚力度嘎嘎足.
1
2
3
4

# 求梯度

将逻辑回归的数学表达式代替二元交叉熵损失函数中的y_hat, 得到一个新的表达式, 在这个新的表达式中对自变量 w和b求偏导..
这个新表达式是个复合函数,可以用链式法则来求导, 具体的求导过程略..

# 交叉熵代码

from numpy import log
def binary_cross_entropy(y, y_hat):
    """
    y     标签值
    y_hat 模型预测值
    """
    loss = - y * log(y_hat) - (1 - y) * log(1 - y_hat)
    return loss
  
print(binary_cross_entropy(0, 0.01))         # 0.01005033585350145
print(binary_cross_entropy(1, 0.99))         # 0.01005033585350145
print(binary_cross_entropy(0, 0.8))          # 1.6094379124341005
print(binary_cross_entropy(1, 0.2))          # 1.6094379124341003
print(binary_cross_entropy(1, 0.00001))      # 11.512925464970229
print(binary_cross_entropy(1, 0.0000000001)) # 23.025850929940457
print(binary_cross_entropy(1, 0))            # inf 无穷大
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 泰坦尼克号实战

就不细说了,我粘贴点代码,标注下需要注意的地方. 特别注意里面的广播操作.emm.

image-20250122184719648

Ps: 我们知道循环越多,效率是越低的.. 针对模型训练求最优w、b的代码. 我们可以使用 矩阵的方式加速模型的训练.. 略.

线性回归
softmax多分类器

← softmax多分类器→

最近更新
01
deepseek本地部署+知识库
02-17
02
实操-微信小程序
02-14
03
教学-cursor深度探讨
02-13
更多文章>
Theme by Vdoing | Copyright © 2023-2025 DC | One Piece