其它排序

# 希尔排序

希尔排序是插入排序变形过来的.

def insert_sort_gap(li, gap):
    for i in range(gap, len(li)):
        j = i - gap
        temp = li[i]
        while j >= 0 and li[j] > temp:  # li[j] > temp大于升序;小于降序
            li[j + gap] = li[j]
            j -= gap
        li[j + gap] = temp
    return li


def shell_sort(li):
    d = len(li) // 2
    while d >= 1:
        insert_sort_gap(li, d)
        d //= 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

时间复杂度: gap不同复杂度不同.

希尔排序(Shell Sort)是一种分组插入排序算法.
首先取一个整数d1= n//2, 将元素分为d1个组, 每组相邻元素之间的距离为d1. 在各组内直接进行插入排序.
取第二个整数d2= d1//2, 重复上述分组排序过程, 直到di=1. 即所有元素在同一组内进行插入排序.

希尔排序每趟并不使某些元素有序, 而是使整体数据越来越接近有序; 最后一趟排序使得所有数据有序.
可以用数学证明,每趟结束后,列表逆序的数越来越少,即越来越接近有序.

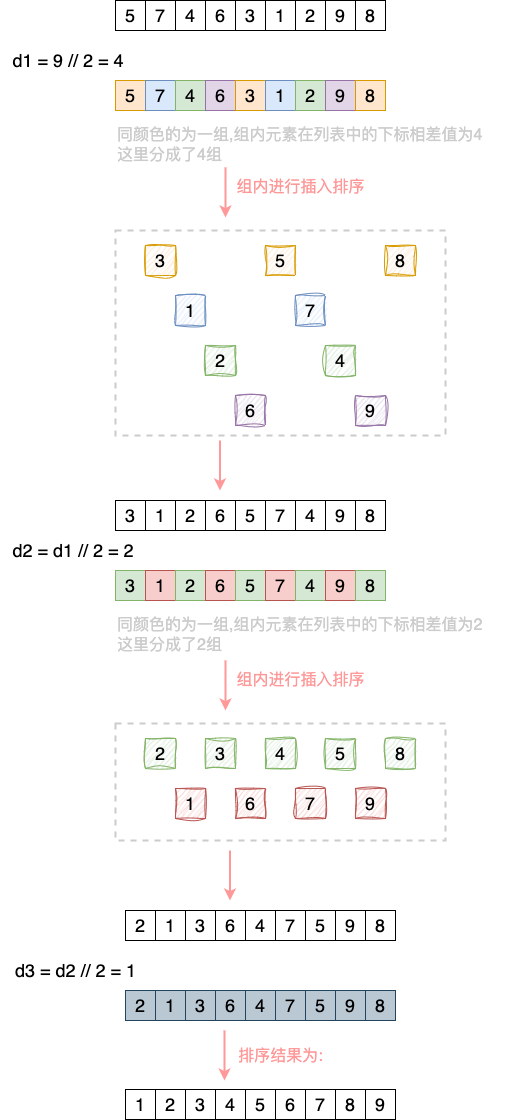
用代码实现希尔排序

"""# -- 插入排序
def insert_sort(li):
    for i in range(1, len(li)): 
        j = i - 1 
        temp = li[i]
        while j >= 0 and li[j] > temp:  # 大于升序;若是小于,降序
            li[j + 1] = li[j]
            j -= 1
        li[j + 1] = temp
    return li
"""
# -- 分组后,每一组内部进行了插入排序
def insert_sort_gap(li, gap):
    for i in range(gap, len(li)):
        j = i - gap
        temp = li[i]
        while j >= 0 and li[j] > temp:
            li[j + gap] = li[j]
            j -= gap
        li[j + gap] = temp
    return li


# -- 进行希尔排序
def shell_sort(li):
    d = len(li) // 2
    while d >= 1:
        insert_sort_gap(li, d)
        d //= 2


if __name__ == '__main__':
    li = list(range(100))
    import random

    random.shuffle(li)
    shell_sort(li)
    print(li)
    
# -- 实验了下,10000个数,插排会花费6s;希尔排序只需要0.06秒.但希尔排序还是比NB三人组里最慢的堆排序慢.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

希尔排序的时间复杂度和选取的gap序列有关!! grap序列不同,时间复杂度不同.就不具体讨论啦.很复杂.
此处的gap, 也就是d 我们用的是列表长度 n//2 n//4 n//8 ...

# 计数排序

需求: 对列表进行排序, 已知列表的数的范围都在0到100之间. 设计时间复杂度为O(n)的算法!!

注: 之前讲到的排序都属于是比较排序.. 可以用数学证明,比较排序最快的时间复杂度是nlogn.
So, 计数排序不是用比较的方法实现的.

时间复杂度: O(n) -- 有很多限制. 需要知道范围,范围大的话废空间.不能对小数进行计数.

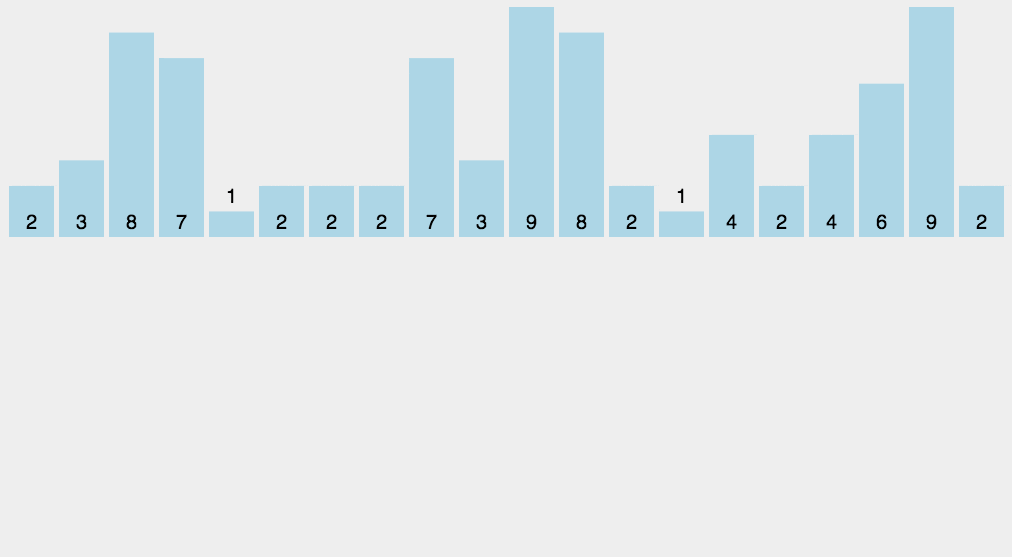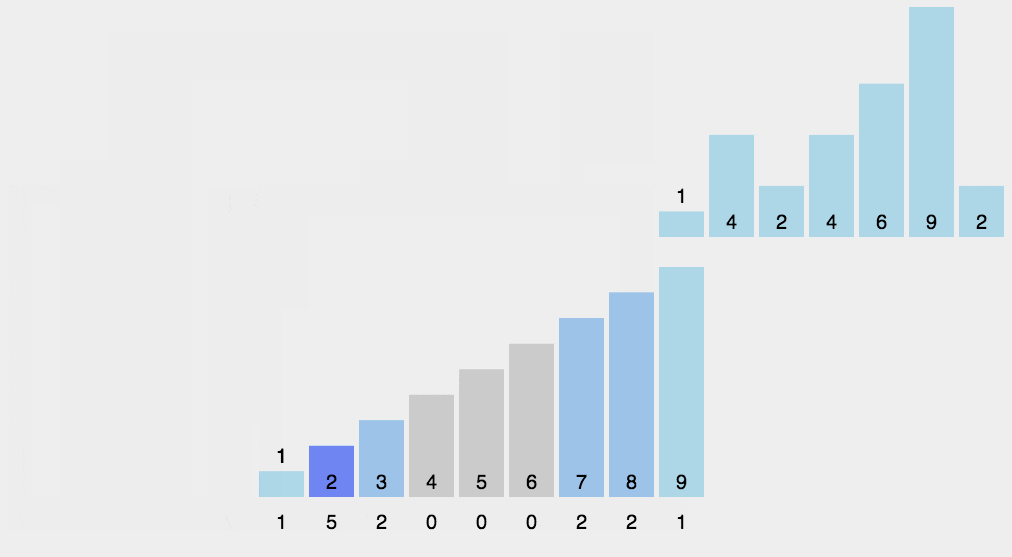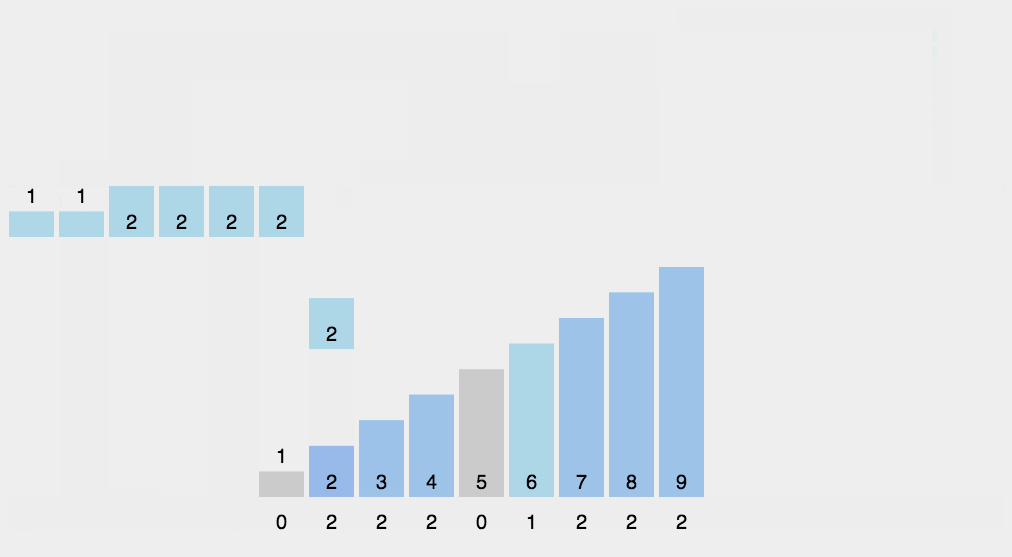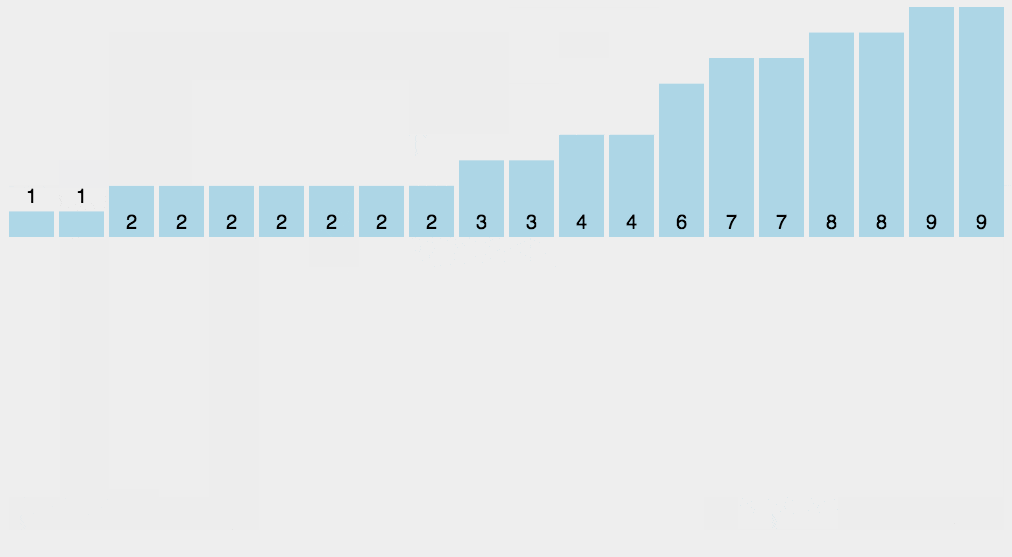
代码实现

# max_count参数:指列表中最大的数是多少.
def count_sort(li, max_count=100):
    # 假设列表的最大数为100,0-100是101个数字.range函数顾头不顾尾.
    count = [0 for _ in range(max_count + 1)]
    # 统计
    for val in li:
        count[val] += 1
    # 清空
    li.clear()
    # 写回
    for index, value in enumerate(count):
        # 有value个index. 若是0个index,li是不会append的.
        for _ in range(value):
            li.append(index)


if __name__ == '__main__':
    import random

    li = [random.randint(0, 100) for _ in range(15)]
    print(li)
    count_sort(li, max_count=100)
    print(li)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

时间复杂度分析: count[val] += 1 执行n次, li.append(index) 执行n次.. So,为2n. 时间复杂度为O(n).

-- 举一反三 --
若不是对数字进行计数排序,而是对字典呢?
{"name":'a',"age":18}
{"name":'b',"age":18}
{"name":'c',"age":16}
{"name":'d',"age":25}
比如说对年龄进行排序.. 我们得知年龄的范围是0-100
那么初始化的列表的下标代表年龄,列表中的每个元素应该是一个列表,遇到年龄相同的字典,就append该字典对象进去!!而不是像数字一样计数了.

1
2
3
4
5
6
7
8

# 桶排序

在计数排序中, 如果元素的范围比较大 (比如1到1亿之间) 如何改进算法?
桶排序 (Bucket Sort): 首先将元素分布在不同桶中, 再对每个桶中的元素进行排序!

时间复杂度: O(nk)

代码实现

# n:多少个桶; max_num:列表中最大的数
def bucket_sort(li, n=100, max_num=10000):
    buckets = [[] for _ in range(n)]  # 创建了n个空桶,桶的编号从0到n-1
    for var in li:
        # -- 求列表中的数放到哪个桶里
        #  `max_num//n` 每个桶里多少个数   `var // (max_num // n)` var放到哪个桶里
        #  有会越界的情况
        #     max_num=9,n=3 分为了编号为0,1,2的三个桶 每个桶里三个数 9//3=3,没有编号为3的桶
        #     max_num=9,n=2 分为了编号为0,1的三个桶 每个桶里四个数 9//4=2,8//4=2,没有编号为2的桶
        #  解决方案,使用min函数,越界的都放到编号最大的那个桶里!
        i = min(var // (max_num // n), n - 1)
        # -- 将列表中的数放到对应的桶里
        buckets[i].append(var)
        # △ 当然可以待列表元素全部放到对应的桶中后,再对每个桶内的元素进行排序.
        # -- 保证桶内的顺序 跟插入排序一个道理.桶中来了一个元素,插入到合适的位置!
        #    list(range(10-1,-1,-1)) --> [9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 10个元素的下标
        for j in range(len(buckets[i]) - 1, 0, -1):  # 从大到小拿到了某个桶内元素的下标
            # 思考,range(len(buckets[i]) - 1, 0, -1) 这里为啥写0不写-1
            # 其一: 桶内只有一个元素时,是该元素自己跟自己比.没意义.
            # 其二: 假设桶内元素是这样的[3,4,5,1]
            #      [3,4,5,1] --> j=3 [3,4,1,5] --> j=2 [3,1,4,5] --> j=1 [1,3,4,5]
            #      当j=0时候,再交换的话,就出事了 --> [5,3,4,1]
            if buckets[i][j] < buckets[i][j - 1]:  # 小于,桶内元素升序,若大于降序
                buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j]
            else:
                break
    # -- 列表排序后的结果
    sorted_li = []
    for buc in buckets:
        sorted_li.extend(buc)
    return sorted_li


if __name__ == '__main__':
    import random

    li = [random.randint(0, 10000) for _ in range(100000)]
    print(bucket_sort(li)[:100])
    
"""
代码可以优化.
上述代码中,是插入后立即对桶进行排序.可以试试,插入完后,再对每个桶使用快排等进行排序.
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

讨论
桶排序的表现取决于数据的分布, 也就是需要根据不同的数据排序时采取不同的分桶策略.

比如一万个数,分为10个桶.而90%的数都处于9000-10000.那么大多数的数据都会分到最后一个桶里.
这时候,应该采取不同的分桶策略,比如处于0-9000的分2个桶,处于9000-10000的分8个桶..

注:n是列表长度,m是桶的个数,k是根据n和m算出来的.简单理解,k表示桶平均多长.具体就不讨论了.
平均情况时间复杂度: O(nk)
最坏情况时间复杂度: O(n^2k)
空间复杂度: O(n+k)

1
2
3
4
5
6
7

# 基数排序

多关键字排序: 假如现在有一个员工表, 先按照年龄进行排序, 若年龄相同, 再按照薪资进行排序.
注: 若年龄薪资都一样,排序后和排序前相对位置是不会变的.这就是稳定性.

对[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48], 是否可看作是多关键字排序?

def list_to_buckets(li, base, iteration):
    buckets = [[] for _ in range(base)]
    for number in li:
        digit = (number // (base ** iteration)) % base
        buckets[digit].append(number)
    return buckets


def buckets_to_list(buckets):
    return [x for buc in buckets for x in buc]


def radix_sort(li, base=10):
    max_val = max(li)
    it = 0
    while base ** it <= max_val:
        li = buckets_to_list(list_to_buckets(li, base, it))
        it += 1
    return li


if __name__ == '__main__':
    import random

    li = list(range(1000))
    random.shuffle(li)
    print(li)
    print(radix_sort(li))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

时间复杂度: O(kn) k指的是分几次桶/最大的数有多少位.
空间复杂度: O(n+k) 跟桶排序的空间复杂度一样!

分桶后依次输出,再分桶再输出.. 直到排序好.
step1: 分了0-9十个桶. 首先按照“个位”分桶, 比如 36 26 46 按照在原列表中的顺序放到了6号桶中.
step2: 依次从十个桶中将数字拿出来.. 先进桶的先出来, 先进先出, 比如 6号桶, 36 26 46 会依次拿出来/输出.
step3: 再按照"十位分桶", 没有十位的,十位数用0表示.. 分完后, 再依次(桶依次,桶中元素依次/先进先出)拿出就是排序好的!!!

代码实现:

def radix_sort(li):
    max_num = max(li)
    # max_num的位数是几,就需要分几次桶 eg: 876 -> 3; 66 -> 2; 10000 -> 5
    # 最简单的方法,用对数向下取整.可以求得分几次桶..
    # 这里用个while来实现. it 为分桶的次数.
    """
    it = 0
    while 10 ** it <= max_num:
        it += 1
    """
    it = 0
    while 10 ** it <= max_num:
        buckets = [[] for _ in range(10)]  # 每次分桶都要初始化这10个桶
        for var in li:
            # -- 根据it的值决定取哪位上的数,并取出来 比如数为987
            # it=0 取个位 987%10
            # it=1 取十位 987//10%10
            # it=2 取百位 987//100%10
            digit = (var // (10 ** it)) % 10
            # -- 取出来的数决定了要分到哪个桶里
            buckets[digit].append(var)
        # for循环结束,意味着这一轮的分桶结束,接着需要将桶中的数据写回li里
        li.clear()  # 清空
        for buc in buckets:
            li.extend(buc)  # 放回

        it += 1


if __name__ == '__main__':
    import random

    li = list(range(1000))
    random.shuffle(li)
    print(li)
    radix_sort(li)
    print(li)
    

"""
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
计数排序: 只有一个桶,只存储单一键值;
桶排序: 每个桶存储一定范围的数值,桶内元素需要排序.只装一次桶.
基数排序: 根据键值的每位数字来分配桶.不需要对桶内元素排序.装多次桶.

基数排序 O(kn) --> k是以10为底,n的log
快排 O(nlogn) --> logn是以2为,n的log
平均分布的情况下,看在哪个范围内,开始时基数比快排快,往后越来越大,是快排比基数快.跟数学有关,就不深究了.(つД`)ノ
而且基数排序跟离散点有关,万一那个最大的数远大于其它数,或者分布不均匀??并且基数排序还得消耗桶.那还是快排好.

扩展:
  字符串分桶,只考虑字母26个桶,考虑ACSII码128个桶 eg: abcd与ab比较,需要ab在后面加0 --> abcd ab00
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

← NB三人组查找习题→