DC's blog
DC
2024-07-08
目录

numpy

Numpy的 核心数据结构 是 多维(可是是一维的,也可以是多维的)数组对象, 简称 ndarray. 它多用来处理数值型(整型,浮点型)数据.
Python的Pandas、tensorflow等模块都依赖于Numpy! So, 学会并掌握numpy的使用迫在眉急.
Ps: 数据结构 - 以某种形式装在数据的容器.

接下来, 我们来康康 ndarray 这个数据结构具备的特性?!

Numpy

# 总结

■ 样子: ndarray [] 、[[],[]] 、 [[[],[]],[[],[]]]
■ 创建: 
  array方法传列表、内置函数(看参数size,shape指定形状) 
  eg: (3,4,5) 第一第二第三个括号里有多少个成员,对应轴axios 0,1,2
■ IO操作: 存读
■ 查看数组
  arr.ndim  arr.shape  arr.size  arr.dtype  arr.nbytes
■ 数组类型转换:
  修改数组类型,减少数组所占内存空间大小
  arr_new = arr.astype('int32') 返回一个新数组,不会影响原数组
■ 数组运算 -- 无需任何for循环,向量化
  + - * / > < >= <= == 两方面  "注:逻辑运算的结果是bool数组哦!!是可以充当数组索引的."
  1> ★ 任何在两个等尺寸数组之间的算数操作都应用了逐元素操作的方式 (Ps:不同尺寸的话,会涉及广播特性,场景不多,不深究)
       大白话:两形状相同的数组进行运算,同一位置的元素一一对应.
  2> ★ 带有标量计算的算术操作,会把计算参数传递给数组的每一个元素
       大白话:数组每一个位置的元素都要与该标量值进行运算.
  注: += -= *= /= 改变的是原数组,So,计算结果的类型若与原数组的数据类型不一致会报错,解决方案有两种: 地板除法、类型转换
● ★ 对numpy数组的索引和切片操作返回的数组都是原数组的视图哦!! 
    why? numpy处理的是大数组,若是复制,会浪费大量内存!! 注:python列表的切片是浅拷贝.
    arr = np.arange(10)
    - 切片被赋值,改变原数组 arr[5:8] = 12  "逐元素操作,多维同理"
    - 切片被引用,相当于贴了个标签,多了对该视图的引用,当我们改变arr_slice时,变化也会体现在原数组上 arr_slice = arr[5:8]
● 基础索引和切片 -- 我们约定此处的索引是某个轴上的单个索引  别死记,找规律!（¯﹃¯）
  我们假设arr数组是n维的,那么对其进行索引和切片时,可操作n个参数,eg: arr[参数1,参数2,..,参数n],
  每个参数对应一个轴,参数1对应数组0轴,参数2对应数组1轴,以此类推.
  每个参数的形式 有两种,可以是单个索引,也可以是切片的形式!!
  ★ 基于上面的说明,先明确一点,就结果而言,索引降维"取出",切片不降维"保留"!
  arr = np.arange(18).reshape((3,2,3))
  - arr[2,1,2] 等同于 arr[2][1][2] -- 结果是一个数   
    分析:取出当前三维数组里的第3个二维数组,再取出这个二维数组里的第2个一维数组,接着取出这个一维数组的第3个数据
  - arr[:2,:1,:2] -- 结果依旧是3维的
    分析:arr[保留当前三维数组里的前两个二维数组,保留每个二维数组的第一行,保留每个一维数组的前两个]
  - arr[:2,:1,2] -- 结果是2维的 PS:等同于arr[:2,:1][:,:,2]
    分析:arr[保留当前三维数组里的前两个二维数组,保留每个二维数组的第一行,取出每个一维数组的第三个元素]
  ps: arr[:2,1,2]、arr[2,:1,:2] 同理.
● 花式索引/神奇索引 -- 真的够神奇的,有些行为的结果跟我们自己想的并不相同
  arr = np.arange(32).reshape((8,4))
  需求:我们想保留该二维数组中 下标为1,5,7,2的行,每一行中的元素按照下标 0,3,1,2的顺序排列.
  - arr[[1,5,7,2],[0,3,1,2]] 结果出人意料,它会根据每个索引列表对应的元素选出一个一维数组
  - 正解: arr[[1,5,7,2]][:,[0,3,1,2]] -- 结果还是个二维数组
  举一反三:
  1> 单独的索引列表不会降维; arr[[1,5,7,2]] - 等同于 arr[[1,5,7,2],:] 保留原二维数组里索引下标为1,5,7,2的一维数组 '取多行'
  2> 索引列表和切片搭配也不会降维; arr[:,[0,3,1,2]]  '取多列'
     - 保留原二维数组里所有一维数组,保留每个一维数组中下标为0,3,1,2的元素“按该顺序保留”
  3> 索引列表和单个索引一起搭配是会降维的! arr[[1,5,7,2],3]
     - [保留] 原二维数组里索引下标为1,5,7,2的一维数组, [取出] 每个一维数组的下标为3的元素
● 数组的索引也可以是bool值数组!!
  现有个二维数组,arr2 = np.arange(12).reshape(3,4)
  Q1: 我想取第一行和第二行 
  A1: arr2[[True,True,False]]  -- 传入的是一个一维bool数组
  Q2: 我想将该二维数组里小于5的值都替换成-1  ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
  A2: arr2[arr2<5]= -1 原arr2是会改变的哦  -- 传入的是一个二维bool数组
  举一反三:
    names = ['Bob','Joe','Will','Bob','Joe']
    data = np.random.randn(5,3)
    Q1:每个人名和data数组中的一行相对应,我们想要选中所有'Bob'对应的行!
    A1:data[names=='Bob']
    Q2:每个人名和data数组中的一行相对应,我们想要选中所有'Bob'和'Will'对应的行!  &是and的意思,｜是or的意思
    A2:data[(names=='Bob') | (names=='Will')]
■ 数组变形 arr.reshape(4,3) 注:变型前和变形后数组容量不可以发生变化
■ 数组转置 ★ 转置的本质是元素索引的互换. 以三维为例, 数组里每个元素的索引位置从 i,j,k 变为 k,j,i
■ 数组级联
  np.concatenate([arr1,arr2],axis = 0)  arr1,arr2两数组在0轴上进行拼接
  np.concatenate([arr1,arr2],axis = 1)  arr1,arr2两数组在1轴上进行拼接
■ where函数 这个函数还蛮有意思的.
  xarr = np.array([1.1,1.2,1.3,1.4,1.5])
  yarr = np.array([2.1,2.2,2.3,2.4,2.5])
  cond = np.array([True,False,True,True,False])
  Q1: 当cond中的元素为True时,我们取xarr中的对应元素值,否则取yarr中的元素.
  A1: np.where(cond,xarr,yarr)
  >> np.where的第二个和第三个参数并不一定是数组,它们还可以是标量.
  Q1: 随机生成一个 "矩阵" 数据,将其中的正值都替换为2,其它不变.
  A1: np.where(arr>0,2,arr)  原数组arr是没有改变的  ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
  A2: arr[arr>0]=2  直接在原数组arr上改变  ※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
■ 数组排序 
  np.short(arr) 返回排序好的新数组;  arr.short() 原地排序.
※ 其它函数
  计算方差、平方根、均值、中位数、去除重复数等等.
  面对多维的数组,在使用这些函数时,去看该函数有无axis参数,有且传递了该参数的话,会沿着axis的方向进行操作.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

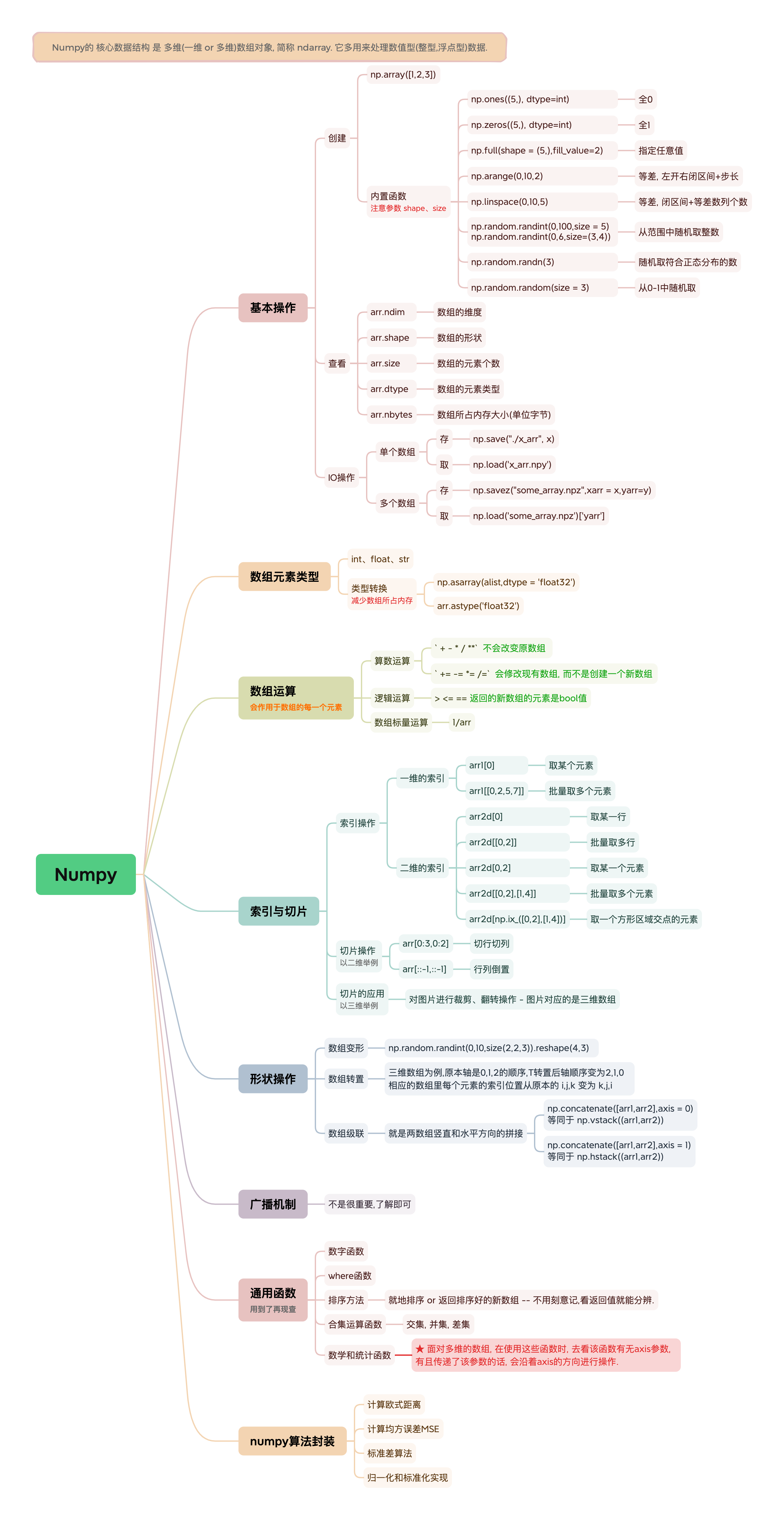
# 基本操作

# 数据创建与查看

创建: array、ones、zeros、full、arange、linspace、random.randint、random.randn、random.random.
查看: arr.ndim、arr.shape、arr.size、arr.stype、arr.nbytes

# 查看
代码 含义 结果
arr.ndim 数组的维度
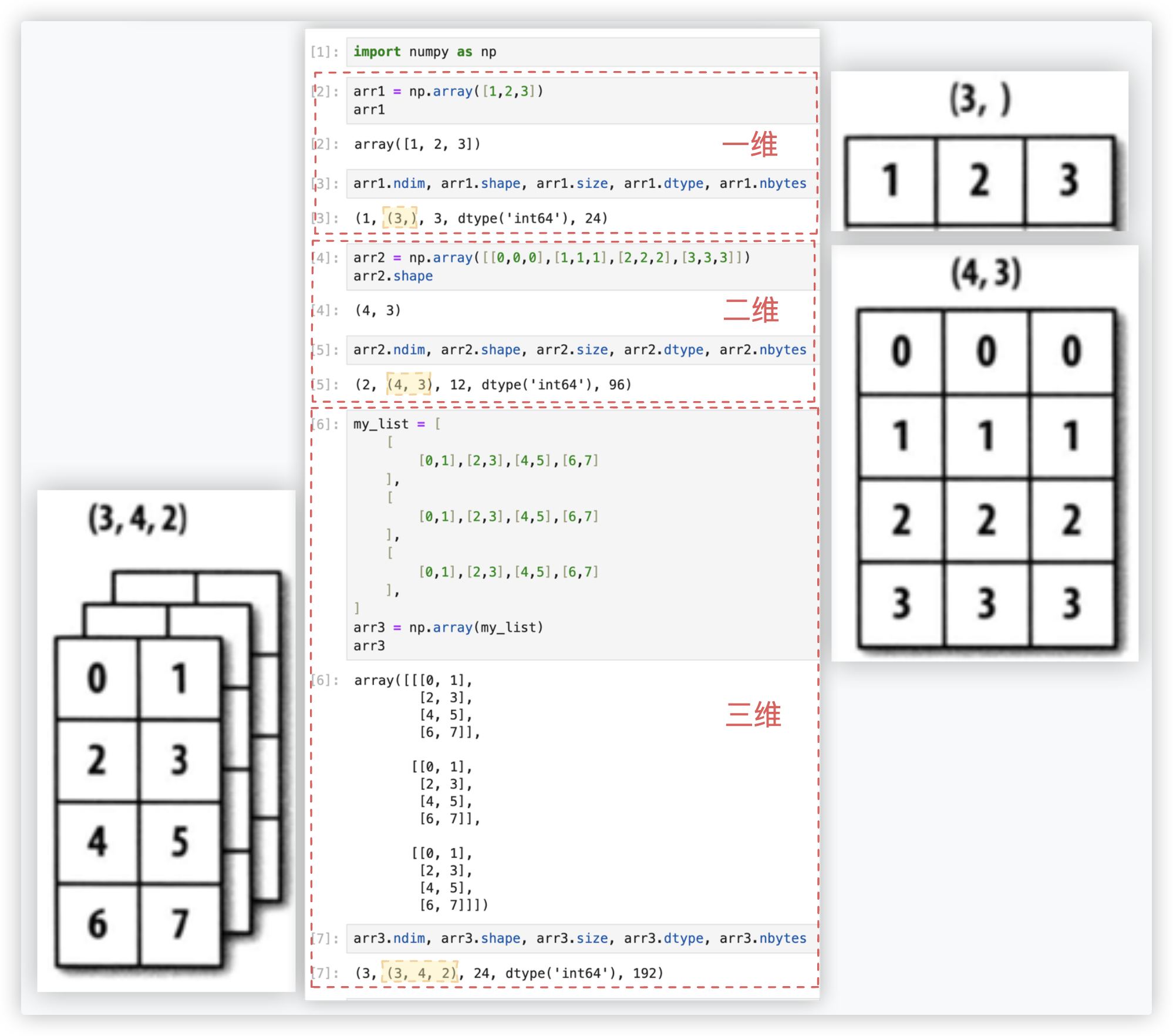
arr.shape 数组的形状 (3,)
(4, 3) -- 4行3列
(3, 4, 2) -- 3个4行2列
arr.size 数组的元素个数/数组的容量 以三维为例: 3*4*2
arr.dtype 数组的元素类型
arr.nbytes 数组所占内存大小(单位字节)
# 创建-array函数

创建数组的最简单的方法就是使用array函数, 它会将Python下的list转换为ndarray.

(*≧ω≦) 多个一维就是二维, 多个二维就是三维.

image-20240721053902756

(*≧ω≦) 敲黑板.
字符串的优先级高于整型、浮点型. so,会自动转换成字符. ★这证明数组中只能存放相同类型的元素.

image-20240721054928989

# 创建-内置函数

利用np中的一些内置函数来创建数组

※ 注意函数有无shape参数 以及 函数的size参数

代码 含义 结果举例
np.ones((5,), dtype=int) 全0 array([1, 1, 1, 1, 1])
np.zeros((5,), dtype=int) 全1 array([0, 0, 0, 0, 0])
np.full(shape = (5,),fill_value=2) 填充指定值 array([2, 2, 2, 2, 2])
np.arange(start = 0,stop = 10,step = 2)
等同于 np.arange(0,10,2)		 等差数列数组
左开右闭区间+步长		 array([0, 2, 4, 6, 8])
np.linspace(start =0,stop = 10,num = 5)
等同于 np.linspace(0,10,5)		 等差数列数组
闭区间+等差数列个数		 np.linspace(start =0,stop = 10,num = 5)
np.random.randint(0,100,size = 5)
np.random.randint(0,6,size=(3,4))		 从范围中随机取整数 array([55, 0, 92, 90, 92])
np.random.randn(3) 随机取符合正态分布的数 array([-1.26839885, 1.19648622, 1.38207117])
np.random.random(size = 3) 从0-1中随机取 array([0.29841786, 0.19743681, 0.83243826])

■ np.ones

>>> import numpy as np
>>> np.ones(5)
array([1., 1., 1., 1., 1.])
>>> np.ones((5,))
array([1., 1., 1., 1., 1.])
>>> np.ones((5,), dtype=int)
array([1, 1, 1, 1, 1])
>>> np.ones((5,2))
array([[1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.]])
1
2
3
4
5
6
7
8
9
10
11
12
13

■ np.zeros

>>> import numpy as np
>>> np.zeros(5)
array([0., 0., 0., 0., 0.])
>>> np.zeros((5,))
array([0., 0., 0., 0., 0.])
>>> np.zeros((5,2),dtype=int)
array([[0, 0],
       [0, 0],
       [0, 0],
       [0, 0],
       [0, 0]])
1
2
3
4
5
6
7
8
9
10
11

■ np.full

>>> import numpy as np
>>> np.full(shape = [2,3],fill_value=2.718)
array([[2.718, 2.718, 2.718],
       [2.718, 2.718, 2.718]])
>>> np.full(shape = [2,3],fill_value='2')
array([['2', '2', '2'],
       ['2', '2', '2']], dtype='<U1')
>>> np.full(shape = [2,3],fill_value=1)
array([[1, 1, 1],
       [1, 1, 1]])
1
2
3
4
5
6
7
8
9
10

■ np.arange、np.linspace

>>> import numpy as np
>>> np.arange(start = 0,stop = 10,step = 2)  # [0,10) 左开右闭区间 步长为2
array([0, 2, 4, 6, 8])
>>> np.arange(0,10,2)
array([0, 2, 4, 6, 8])
>>>
>>>
>>> np.linspace(start =0,stop = 10,num = 5)  # [0,10] 闭区间 等差数列个数为5个
array([ 0. ,  2.5,  5. ,  7.5, 10. ])
>>> np.linspace(0,10,5)
array([ 0. ,  2.5,  5. ,  7.5, 10. ])
1
2
3
4
5
6
7
8
9
10
11

注: 可查看这两函数的参数和注释, 你会发现没有shape这参数, 证明 等差数组 只能是一维的.

■ 随机取

>>> import numpy as np
>>> np.random.randint(0,100,size = 5)
array([55,  0, 92, 90, 92])
>>> np.random.randn(3)
array([-1.26839885,  1.19648622,  1.38207117])
>>> np.random.random(size = 3)
array([0.29841786, 0.19743681, 0.83243826])
1
2
3
4
5
6
7

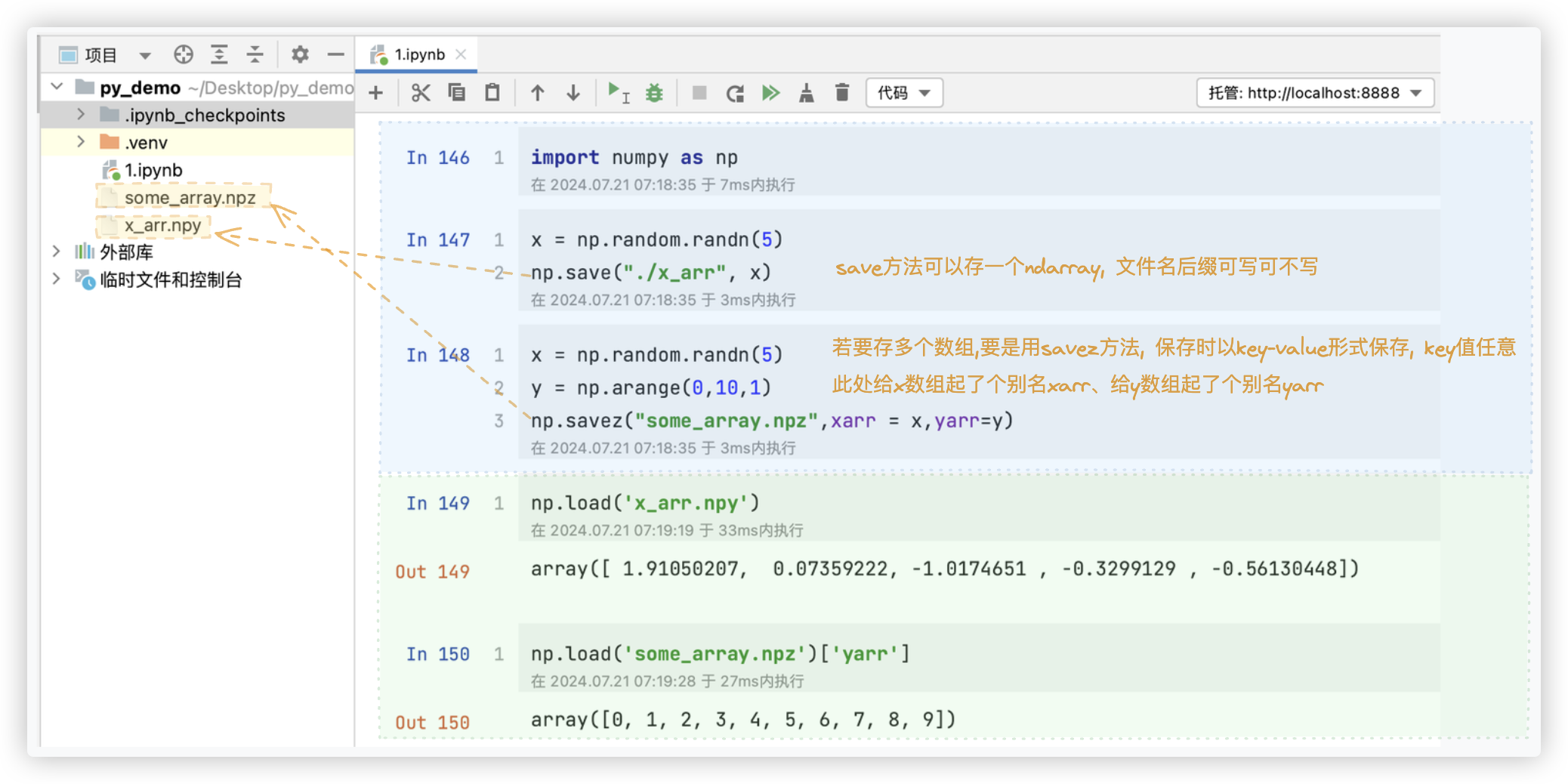
# IO操作

将数组存文件中, 从文件中读取数组

存 - save ; savez - save方法保存一个ndarray到一个npy文件, 也可以使用savez将多个array保存到一个.npz文件中 读 - load

image-20240721072724060

补充: 若想将数组存储到txt、csv文件中, 有个前提 - 数组中的元素都必须是数字类型.

import numpy as np

arr = np.random.randint(0, 10, size=(3, 4))
# 储存数组到txt文件, csv同理
np.savetxt("arr.txt", arr, delimiter=',')  # np.savetxt(文件路径,数组,分隔符)
# 读取txt文件, delimiter为分隔符(默认是" ")
res = np.loadtxt("arr.txt", delimiter=',')
print(res)

"""
[[8. 8. 4. 3.]
 [3. 5. 1. 8.]
 [8. 2. 1. 6.]]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 数组元素类型

三种类型 + 类型转换

1> int: int8、int16、int32、int64.
2> float: float16、float32、float64.
3> str

注: Int64 指每个元素占用64个比特位, 即8个字节.

进行类型转换

>>> import numpy as np
>>> alist = [1,3,5,7,2,9,0]
>>> np.asarray(alist,dtype = 'float32')
array([1., 3., 5., 7., 2., 9., 0.], dtype=float32)
>>>
>>>
>>> arr = np.random.randint(0,10,size = 5,dtype = 'int16') 
>>> arr.astype('float32') 
array([4., 6., 8., 5., 9.], dtype=float32)
1
2
3
4
5
6
7
8
9

★ 类型转换的作用: 通过修改数组的数据类型可以减少数组所占内存大小.

>>> import numpy as np
>>> arr = np.random.randint(0,10,size = 5)
>>> arr.dtype
dtype('int64')
>>> arr.nbytes
40
>>> arr_int32 = arr.astype('int32')  # 返回一个新数组
>>> arr_int32.dtype
dtype('int32')
>>> arr_int32.nbytes
20
>>> arr.nbytes  # 证明类型转换不会影响原数组
40
1
2
3
4
5
6
7
8
9
10
11
12
13

注: int8, 2^8=256, 证明存的最大整数是256.. 若存的整数值大于这个数, 不会报错, 但该元素的值会被改变, 这是不允许的!
So, 类型转换时, 一定要注意这个问题. 我们通常会使用 int32, int64.

# 数组运算

数组之间一些常见的运算

以下示例中参与数组运算的数组, shape形状是一致的. 那shape不一致,还能运算吗? 暂且不探究.

★ 这些运算都作用于数组中的每一个元素!

# 算数运算

+ - * / ** 不会改变原数组
+= -= *= /= 会修改现有数组, 而不是创建一个新数组

+ - * / **

>>> import numpy as np
>>> arr1 = np.array([1,2,3,4,5])
>>> arr2 = np.array([2,3,1,5,9])
>>> arr1 - arr2
array([-1, -1,  2, -1, -4])
>>> arr1 * arr2
array([ 2,  6,  3, 20, 45])
>>> arr1 / arr2
array([0.5       , 0.66666667, 3.        , 0.8       , 0.55555556])
>>> arr1**arr2
array([      1,       8,       3,    1024, 1953125])
1
2
3
4
5
6
7
8
9
10
11

+= -= *= /=

>>> import numpy as np
>>> arr1 = np.arange(5)
>>> arr1
array([0, 1, 2, 3, 4])
>>> arr1 += 5
>>> arr1
array([5, 6, 7, 8, 9])
>>>
>>>
>>> arr2 = np.arange(5)
>>> arr2
array([0, 1, 2, 3, 4])
>>> arr2 -= 5
>>> arr2
array([-5, -4, -3, -2, -1])
>>>
>>>
>>> arr3 = np.arange(5)
>>> arr3
array([0, 1, 2, 3, 4])
>>> arr3 *= 5
>>> arr3
array([ 0,  5, 10, 15, 20])
>>>
>>>
>>> arr4 = np.arange(11)
>>> arr4
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
>>> arr4 /= 5  # arr /= 5的结果可能是浮点型,与当前数组arr元素的数据类型int不一致,所以就报错啦!
Traceback (most recent call last):
  File "<pyshell#54>", line 1, in <module>
    arr4 /= 5
numpy._core._exceptions._UFuncOutputCastingError: Cannot cast ufunc 'divide' output from dtype('float64') to dtype('int64') with casting rule 'same_kind'
>>> # 解决方案: 1> //地板除法; 2> 类型转换
>>> arr4 //= 5
>>> arr4
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2])
>>>
>>> arr4 = np.arange(11)
>>> arr4_float32 = arr4.astype('float32')
>>> arr4_float32 /= 5
>>> arr4_float32
array([0. , 0.2, 0.4, 0.6, 0.8, 1. , 1.2, 1.4, 1.6, 1.8, 2. ],dtype=float32)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# 逻辑运算

返回布尔值

>>> import numpy as np
>>> arr1 = np.array([1,2,3,4,5])
>>> arr2 = np.array([1,0,2,3,5])
>>> arr1 < 5
array([ True,  True,  True,  True, False])
>>> arr1 >= 5
array([False, False, False, False,  True])
>>> arr1 == 5
array([False, False, False, False,  True])
>>> arr1 == arr2
array([ True, False, False, False,  True])
>>> arr1 > arr2
array([False,  True,  True,  True, False])
>>>
>>>
>>> arr3 = np.random.randint(0,6,size=(3,4))
>>> arr3
array([[5, 0, 5, 0],
       [4, 0, 0, 4],
       [1, 4, 2, 2]])
>>> arr3 >= 5
array([[ True, False,  True, False],
       [False, False, False, False],
       [False, False, False, False]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 数组标量计算

数组与标量的算术运算 也会将标量值 传播到各个元素

>>> import numpy as np
>>> arr = np.arange(1,10)
>>> arr
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> 1/arr
array([1.        , 0.5       , 0.33333333, 0.25      , 0.2       ,
       0.16666667, 0.14285714, 0.125     , 0.11111111])
>>> arr + 5
array([ 6,  7,  8,  9, 10, 11, 12, 13, 14])
>>> arr * 5
array([ 5, 10, 15, 20, 25, 30, 35, 40, 45])
1
2
3
4
5
6
7
8
9
10
11

# 索引与切片

将数组中局部的数据进行定位和提取

# 索引操作

细心的你一定会发现, 批量操作时, 索引值是列表.

ps: 索引访问后重新赋值就是修改 暂略.

# 一维的索引
>>> arr1 = np.arange(1,11)
>>> arr1
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
>>> arr1[0]  # 取某个元素
np.int64(1)
>>> arr1[[0,2,5,7]]  # 批量取多个元素
array([1, 3, 6, 8])
1
2
3
4
5
6
7
# 二维的索引

image-20240721144215706

★ 注: 就上图的二维数组而言, axis表明数组层级. axis=0, 该轴上的成员有4个; axis=1, 该轴上的成员有5个. arr2d.shape --> (4, 5)

应用 公式
取某一行 arr2d[0]
批量取多行 arr2d[[0,2]]
取某一个元素 arr2d[0,2]
批量取多个元素 arr2d[[0,2],[1,4]]
取一个方形区域交点的元素 arr2d[np.ix_([0,2],[1,4])]

验证如下: 注意哦,批量时索引值都是列表

>>> arr2d
array([[  1,   3,   5,   7,   9],
       [  2,   4,   6,   8,  10],
       [ 12,  18,  22,  23,  37],
       [123,  55,  17,  88, 103]])
>>> arr2d[0]
array([1, 3, 5, 7, 9])
>>> arr2d[[0,2]]
array([[ 1,  3,  5,  7,  9],
       [12, 18, 22, 23, 37]])
>>> arr2d[0,2]  # 等同于 arr2d[-4,-3]
np.int64(5)
>>> # 第一个列表里是行,第二个列表里是列,需组合下 0,1两线交点的元素; 2,4两线交点的元素.
>>> # 一点思考:可以简单理解 第一个列表是从axis=0上取, 第二个列表是从axis=1上取.
>>> arr2d[[0,2],[1,4]]  
array([ 3, 37])
>>> # 第一个列表里是代提取元素的行标,第二个列表里是待提取元素的列标, 无需组合, 此处是4条线交点的元素.
>>> arr2d[np.ix_([0,2],[1,4])]  
array([[ 3,  9],
       [18, 37]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 切片操作

此示例对应的是二维数据

应用 公式
切行 arr[0:3]
切列 arr[:,0:2]
切行切列 arr[0:3,0:2]
行倒置: 根据横向中心轴进行180度翻转 (二维) arr[::-1]
列倒置: 根据竖向中心轴进行180度翻转 (二维) arr[:,::-1]
行列倒置 arr[::-1,::-1]

实验如下:

>>> arr = np.arange(1,43).reshape(6,7)
>>> arr[0:3]
array([[ 1,  2,  3,  4,  5,  6,  7],
       [ 8,  9, 10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19, 20, 21]])
>>> arr[:,0:2]
array([[ 1,  2],
       [ 8,  9],
       [15, 16],
       [22, 23],
       [29, 30],
       [36, 37]])
>>> arr[0:3,0:2]
array([[ 1,  2],
       [ 8,  9],
       [15, 16]])
>>> arr[::-1]
array([[36, 37, 38, 39, 40, 41, 42],
       [29, 30, 31, 32, 33, 34, 35],
       [22, 23, 24, 25, 26, 27, 28],
       [15, 16, 17, 18, 19, 20, 21],
       [ 8,  9, 10, 11, 12, 13, 14],
       [ 1,  2,  3,  4,  5,  6,  7]])
>>> arr[:,::-1]
array([[ 7,  6,  5,  4,  3,  2,  1],
       [14, 13, 12, 11, 10,  9,  8],
       [21, 20, 19, 18, 17, 16, 15],
       [28, 27, 26, 25, 24, 23, 22],
       [35, 34, 33, 32, 31, 30, 29],
       [42, 41, 40, 39, 38, 37, 36]])
>>> arr[::-1,::-1]
array([[42, 41, 40, 39, 38, 37, 36],
       [35, 34, 33, 32, 31, 30, 29],
       [28, 27, 26, 25, 24, 23, 22],
       [21, 20, 19, 18, 17, 16, 15],
       [14, 13, 12, 11, 10,  9,  8],
       [ 7,  6,  5,  4,  3,  2,  1]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 切片操作的应用

对图片进行裁剪、翻转操作 - 图片对应的是三维数组

用plt模块打开的某张图长下面这个样子.

image-20240721164052797

import matplotlib.pyplot as plt

img_arr = plt.imread('./lufei.jpg')
# (675, 1200, 3) 
# - 就图片而言, 675是图片中的行,1200是图片中的列,3是每个点的RGB
# - 就数组而言, 675个1200行2列
print(img_arr.shape)  
plt.imshow(img_arr)
plt.show()
plt.imshow(img_arr[200:400, 200:400, :])  # 图片裁剪
plt.show()
plt.imshow(img_arr[::-1, :, :])  # 图片上下翻转 - 沿着图片下边呈镜像
plt.show()
plt.imshow(img_arr[:, ::-1, :])  # 图片左右翻转 - 沿着图片左边呈镜像
plt.show()
plt.imshow(img_arr[::-1, ::-1, :])  # 图片上下左右翻转
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 形状操作

该部分很重要,在后面的机器学习的图片识别中会应用到; 建模中也会规定传入的形状是咋样的.

# 数组变形

变型前和变形后数组容量不可以发生变化

>>> import numpy as np
>>> arr1 = np.random.randint(0,10,size=(2,2,3))
>>> arr1
array([[[6, 5, 2],
        [6, 3, 9]],
       [[2, 2, 1],
        [0, 9, 2]]])
>>> arr1.reshape(4,3)  # 等同于 arr1.reshape(-1,3) -1会自动计算2*2
array([[6, 5, 2],
       [6, 3, 9],
       [2, 2, 1],
       [0, 9, 2]])
>>> # 同理, arr1.reshape(2,6) 等同于 arr1.reshape(2,-1)
1
2
3
4
5
6
7
8
9
10
11
12
13

# 数组转置

要弄明白转置就得弄清楚 数组的索引、axis轴..

★ 转置的本质是元素索引的互换. 以三维为例, 数组里每个元素的索引位置从 i,j,k 变为 k,j,i

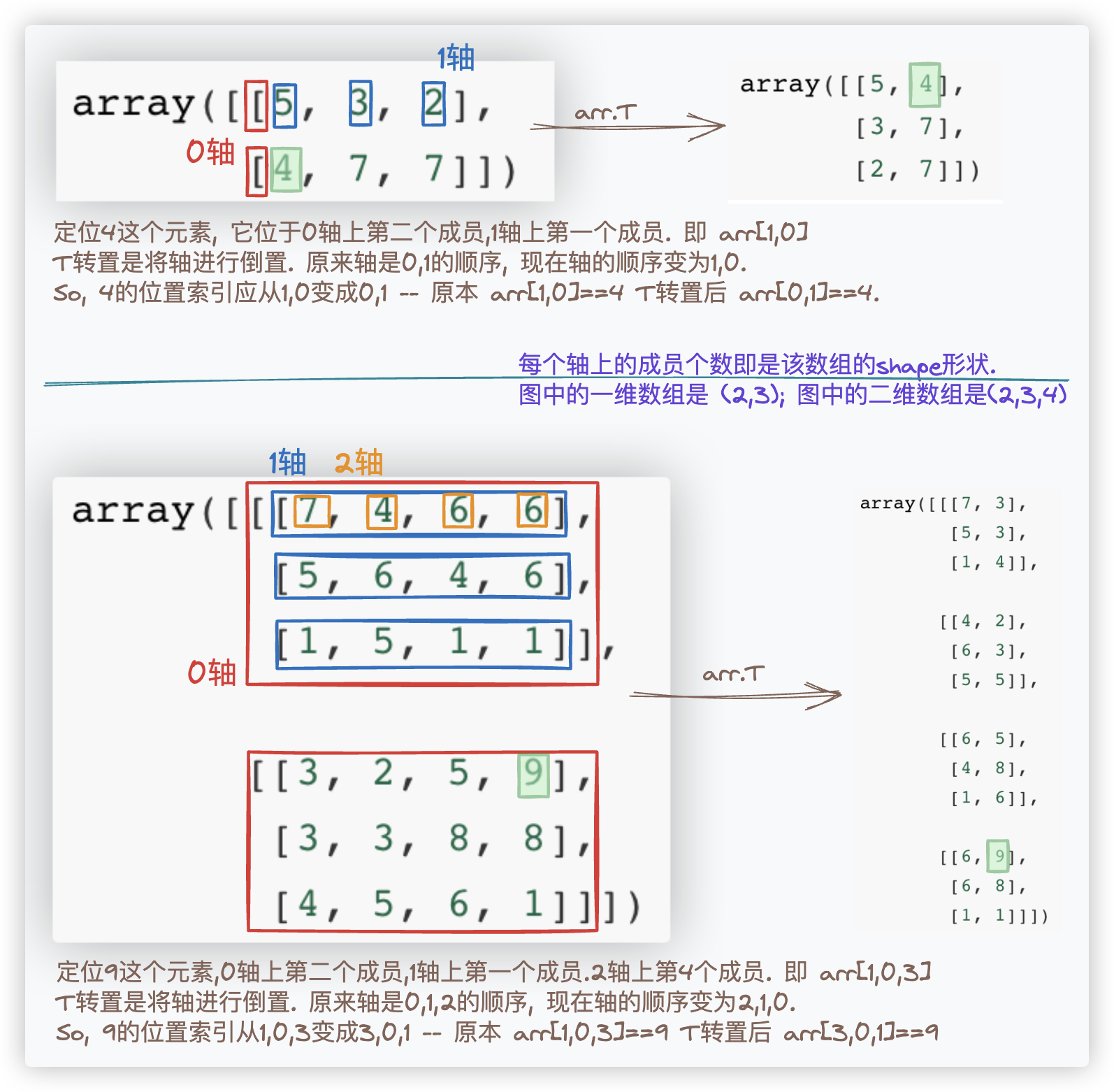
image-20240722101005199

一维数组的验证如下:

>>> import numpy as np
>>> arr1 = np.random.randint(0,10,size = (2,3))
>>> arr1
array([[5, 3, 2],
       [4, 7, 7]])
>>> arr1.T
array([[5, 4],
       [3, 7],
       [2, 7]])
1
2
3
4
5
6
7
8
9

二维数组的验证如下:

>>> import numpy as np
>>> arr2 = np.random.randint(0,10,size = (2,3,4))
>>> arr2
array([[[7, 4, 6, 6],
        [5, 6, 4, 6],
        [1, 5, 1, 1]],

       [[3, 2, 5, 9],
        [3, 3, 8, 8],
        [4, 5, 6, 1]]])
>>> arr2.T
array([[[7, 3],
        [5, 3],
        [1, 4]],

       [[4, 2],
        [6, 3],
        [5, 5]],

       [[6, 5],
        [4, 8],
        [1, 6]],

       [[6, 9],
        [6, 8],
        [1, 1]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 数组级联

两数组进行拼接

>>> import numpy as np
>>> arr1 = np.array([[1,2,3],[4,5,6]])
>>> arr2 = np.array([[7,8,9],[10,11,12]])
>>> np.concatenate([arr1,arr2],axis = 0)  # arr1,arr2两数组在0轴上进行拼接
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])
>>> np.concatenate([arr1,arr2],axis = 1)  # arr1,arr2两数组在1轴上进行拼接
array([[ 1,  2,  3,  7,  8,  9],
       [ 4,  5,  6, 10, 11, 12]])
>>>
>>> # 两数组在竖直方向堆叠,等同于上面的np.concatenate([arr1,arr2],axis = 0)
>>> np.vstack((arr1,arr2))  
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])
>>> # 两数组在水平方向堆叠,等同于上面的np.concatenate([arr1,arr2],axis = 1)
>>> np.hstack((arr1,arr2))
array([[ 1,  2,  3,  7,  8,  9],
       [ 4,  5,  6, 10, 11, 12]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

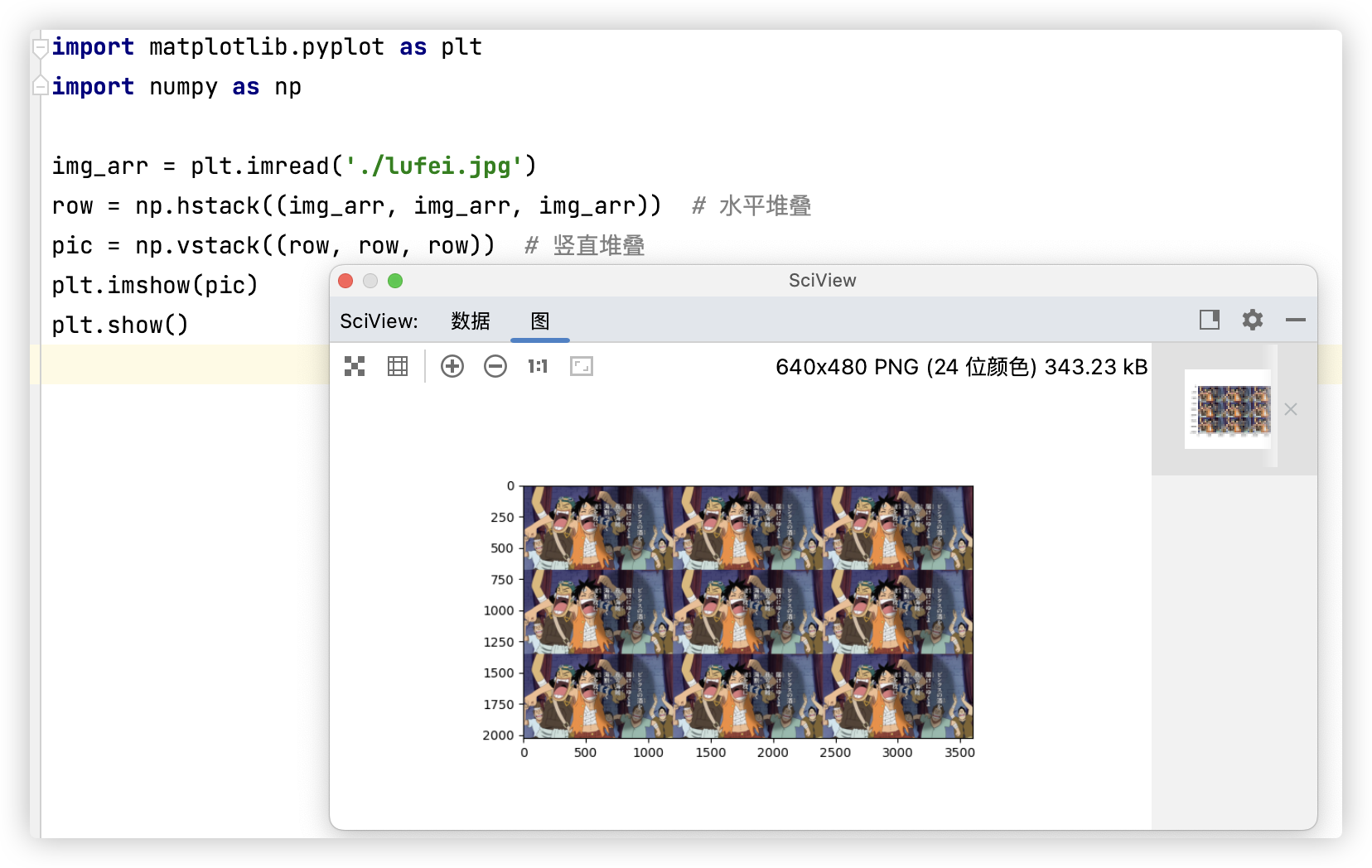
应用: 利用级联复制图片实现九宫格.

image-20240722103605653

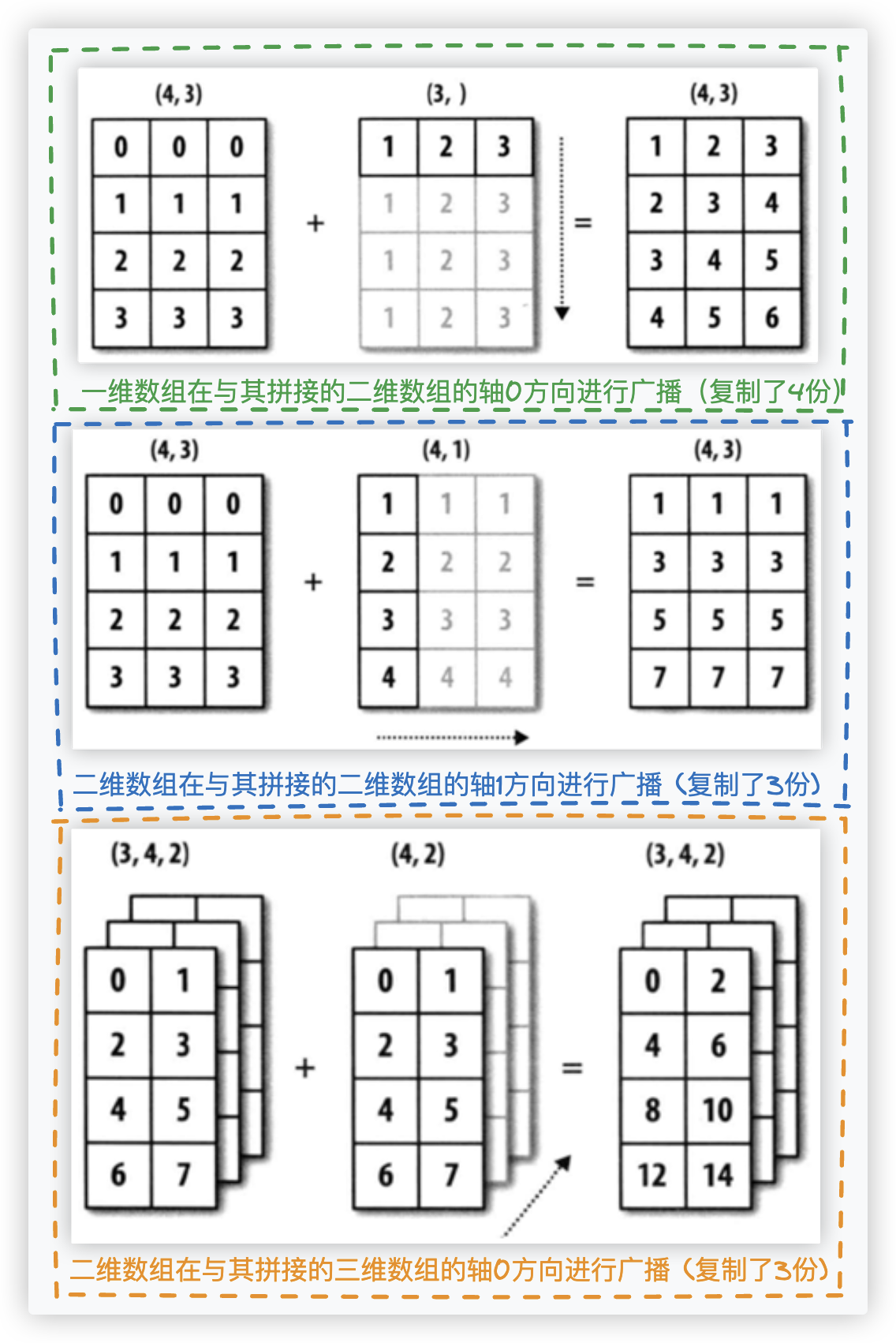
# 广播机制

不是很重要,了解即可

image-20240722105512697

# 通用函数

Hhhh (´･Д･)」

# 数字函数

用到了再查

>>> import numpy as np
>>> arr = np.array([1,2,3])
>>> np.abs(arr)  # 计算数组各元素的绝对值
array([1, 2, 3])
>>> np.sqrt(arr)  # 计算数组各元素的平方根
array([1.        , 1.41421356, 1.73205081])
>>> np.square(arr)  # 计算数组各元素的平方
array([1, 4, 9])
>>> np.exp(arr)  # 计算数组各元素的指数值
array([ 2.71828183,  7.3890561 , 20.08553692])
>>> np.log(arr)  # 计算数组各元素的自然对数
array([0.        , 0.69314718, 1.09861229])
1
2
3
4
5
6
7
8
9
10
11
12

# where函数

Bingo~

■ 根据cond选择的元素形成的新数组.

>>> import numpy as np
>>> arr1 = np.array([1, 2, 3, 4, 5])
>>> arr2 = np.array([10, 20, 30, 40, 50])
>>> cond = np.array([True, False, True, False, True])
>>> # cond数组中的True表示选择arr1对应位置的元素, False表示选择 arr2 对应位置的元素. 
>>> np.where(cond, arr1, arr2)
array([ 1, 20,  3, 40,  5])
1
2
3
4
5
6
7

■ 取出小于指定值的元素的索引

>>> import numpy as np
>>> # 一维
>>> arr1 = np.array([1,2,3,4])
>>> np.where(arr1<3)
(array([0, 1]),)
>>>
>>>
>>> # 二维
>>> arr2 = np.arange(0,12).reshape(2,2,3)
>>> arr2
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])
>>> np.where(arr2<7)
(array([0, 0, 0, 0, 0, 0, 1]), array([0, 0, 0, 1, 1, 1, 0]), array([0, 1, 2, 0, 1, 2, 0]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

■ arr中小于指定值的元素返回元素本身,不满足的元素返回值-1

>>> import numpy as np
>>> # 一维
>>> arr1 = np.array([1,2,3,4])
>>> np.where(arr1<3,arr1,-1)
array([ 1,  2, -1, -1])
>>>
>>>
>>> # 二维
>>> arr2 = np.arange(0,12).reshape(2,2,3)
>>> arr2
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])
>>> np.where(arr2<7,arr2,-1)
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6, -1, -1],
        [-1, -1, -1]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 排序方法

就地排序 or 返回排序好的新数组 -- 不用刻意记,看返回值就能分辨.

PS: 默认是从小到大排序. 好像只能从小到大排,待考究.哈哈哈

■ 返回排序好的新数组, 原数组不变

>>> import numpy as np
>>> arr = np.random.randint(0,20,size=(2,2,3))
>>> arr
array([[[ 5, 14,  8],
        [ 6, 17,  2]],

       [[15, 10,  8],
        [14,  3, 18]]])
>>> np.sort(arr)  # 你可以发现它排的是最里层的中括号里的元素
array([[[ 5,  8, 14],
        [ 2,  6, 17]],

       [[ 8, 10, 15],
        [ 3, 14, 18]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14

■ 就地排序, 改变原数组

>>> import numpy as np
>>> arr = np.random.randint(0,20,size=(2,2,3))
>>> arr
array([[[ 5, 14,  8],
        [ 6, 17,  2]],

       [[15, 10,  8],
        [14,  3, 18]]])
>>> arr.sort()  # 你可以发现它排的是最里层的中括号里的元素
>>> arr
array([[[ 5,  8, 14],
        [ 2,  6, 17]],

       [[ 8, 10, 15],
        [ 3, 14, 18]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

■ 返回数组元素从小到大排序索引

>>> import numpy as np
>>> # 一维
>>> arr = np.random.randint(0,20,8)
>>> arr
array([16,  0,  5,  8,  6, 11, 18, 15])
>>> arr.argsort()
array([1, 2, 4, 3, 5, 7, 0, 6])  # 原数组索引为1的元素,原数组索引为2的元素..以此类推
>>>
>>>
>>> # 三维
>>> arr = np.random.randint(0,20,size=(2,2,3))
>>> arr
array([[[15,  4,  1],
        [13, 15,  6]],

       [[16, 17,  0],
        [10, 19, 11]]])
>>> arr.argsort()  # 与上面同理
array([[[2, 1, 0],
        [2, 0, 1]],

       [[2, 0, 1],
        [0, 2, 1]]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 合集运算函数

交集, 并集, 差集

>>> import numpy as np
>>> # 一维
>>> A = np.array([2,4,6,8])
>>> B = np.array([3,4,5,6])
>>> np.intersect1d(A,B)  # 交集
array([4, 6])
>>> np.union1d(A,B)  # 并集
array([2, 3, 4, 5, 6, 8])
>>> np.setdiff1d(A,B)  # 差级(A中有,B中没有)
array([2, 8])
>>>
>>>
>>> # 三维
>>> A = np.random.randint(0,20,size=(2,2,3))
>>> A
array([[[ 0,  9,  7],
        [10,  7, 19]],

       [[13, 19,  8],
        [ 6,  9, 10]]])
>>> B = np.random.randint(0,20,size=(2,2,3))
>>> B
array([[[ 0,  9,  5],
        [10, 10, 11]],

       [[15, 12,  7],
        [13,  6, 11]]])
>>> np.intersect1d(A,B)
array([ 0,  6,  7,  9, 10, 13])
>>> np.union1d(A,B)
array([ 0,  5,  6,  7,  8,  9, 10, 11, 12, 13, 15, 19])
>>> np.setdiff1d(A,B)
array([ 8, 19])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 数学和统计函数

还蛮多的Hhh, 用到什么再来查, 不用记.

公式 含义
arr.min() 计算最小值
arr.max() 计算最大值
arr.mean() 计算平均值
np.median(arr) 计算中位数
np.sum(arr) 求和
np.std(arr) 求标准差
np.var(arr) 求方差
np.cumsum(arr) 计算累加和
np.argmin(arr) 计算最小值的索引
np.argmax(arr) 计算最大值的索引
np.argwhere(arr>13) 返回元素值大于13的元素的索引
np.corrcoef(arr) 计算相关性系数 (何为相关性系数? 暂略)
np.unique(arr) 去除重复数据

★ 面对多维的数组, 在使用这些函数时, 去看该函数有无axis参数, 有且传递了该参数的话, 会沿着axis的方向进行操作.

>>> import numpy as np
>>> # 一维
>>> arr = np.random.randint(1,20,10)
>>> arr
array([11,  8, 18,  2,  9, 11,  7, 17, 14,  6])
>>> arr.min()  # 最小
np.int64(2)
>>> arr.max()  # 最大
np.int64(18)
>>> arr.mean()  # 平均值
np.float64(10.3)
>>> np.median(arr)  # 中位数
np.float64(10.0)
>>> np.sum(arr)  # 求和
np.int64(103)
>>> np.std(arr)  # 标准差
np.float64(4.73392015141785)
>>> np.var(arr)  # 方差
np.float64(22.410000000000004)
>>> np.cumsum(arr)  # 累加和
array([ 11,  19,  37,  39,  48,  59,  66,  83,  97, 103])
>>> np.argmin(arr)  # 最小值索引
np.int64(3)
>>> np.argmax(arr)  # 最大值索引
np.int64(2)
>>> np.argwhere(arr>13)  # 大于13的元素的索引
array([[2],
       [7],
       [8]])
>>> np.corrcoef(arr)  # 相关性系数
np.float64(1.0)
>>> np.unique(arr)
array([ 2,  6,  7,  8,  9, 11, 14, 17, 18])
>>>
>>>
>>> # 二维
>>> arr = np.random.randint(1,20,size=(3,4))
>>> arr
array([[12,  4, 14,  2],
       [ 5,  4,  7,  4],
       [10,  8,  3,  7]])
>>> np.sum(arr)
np.int64(80)
>>> np.sum(arr,axis=0)
array([27, 16, 24, 13])
>>> np.sum(arr,axis=1)
array([32, 20, 28])
>>> arr.mean()
np.float64(6.666666666666667)
>>> arr.mean(axis=0)
array([9.        , 5.33333333, 8.        , 4.33333333])
>>> arr.mean(axis=1)
array([8., 5., 7.])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

# numpy算法封装

封装是个好东西.Hhh

# 计算欧式距离

欧式距离是用来计算两个向量之间的距离的常用方法.

例如坐标系中有两点a(x1,y1)和b(x2,y2), 那么ab两点距离计算公式为: (x1-x2)^2 +(y1-y2)^2 然后开根号

import numpy as np


def euclidean_distance(a, b):
    # np.square平方 ; np.sum和 ; np.sqrt开平方
    return np.sqrt(np.sum(np.square(a - b)))


if __name__ == '__main__':
    a = np.array([1, 2, 3])
    b = np.array([4, 5, 6])
    dist = euclidean_distance(a, b)
    print(dist)
1
2
3
4
5
6
7
8
9
10
11
12
13

# 计算均方误差MSE

机器学习中会用到.

均方误差是指对于一组样本真实结果和预测结果, 先计算它两差异平方, 然后累加, 最后除以样本数量的结果。

import numpy as np


def mean_squared_error(y_true, y_pred):
    squared_errors = np.square(y_true - y_pred)  # 计算差异平方 [0.01, 0.01, 0.04, 0.04, 0.01]
    sum_squared_errors = np.sum(squared_errors)  # 累加差异平方 0.1100000000000001
    mse = sum_squared_errors / len(y_true)  # 计算均方误差 0.02200000000000002

    return mse


if __name__ == '__main__':
    y_true = np.array([1, 2, 3, 4, 5])
    y_pred = np.array([1.1, 1.9, 3.2, 3.8, 5.1])
    mse = mean_squared_error(y_true, y_pred)
    print("均方误差：", mse)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 标准差算法

表明样本的 稳定度/离散程度

离均差平方和 除以 样本数量 是方差, 方差再开根号就是标准差.

import numpy as np


def standard_deviation(data):
    mean = np.mean(data)
    variance = np.sum((data - mean) ** 2) / data.size
    std_dev = np.sqrt(variance)
    return std_dev


if __name__ == '__main__':
    data = np.array([1, 2, 3, 4, 5])
    print("数据的标准差：", standard_deviation(data))  # 1.4142135623730951
1
2
3
4
5
6
7
8
9
10
11
12
13

# 归一化和标准化实现

归一化和标准化都是数据预处理技术, 分别用于将数据转换到 特定的范围、特定的分布.

# 归一化

举个例子, [1,2,3,4,5] ; [99,210,310,499,501] 两个数组, 里面元素的单位可能是米,也可能是厘米毫米..
你在不知道它们单位的时候, 是比较不了的! So, 我们要想办法去除 纲量(eg:单位) 的影响. 使它们在数值上有可比性.

归一化 - 将数据缩放到一个固定的区间[0, 1].
通常是通过使用一组数据中的每一个元素减去该组数据的最小值然后除以这组数据的最大值和最小值之间的差来实现的.

>>> import numpy as np
>>> def normalize(data):
        min_val = np.min(data)
        max_val = np.max(data)
        range_val = max_val - min_val
        normalized_data = (data - min_val) / range_val
        return normalized_data

>>> data_m = np.array([1, 2, 3, 4, 5])
>>> normalize(data_m)
array([0.  , 0.25, 0.5 , 0.75, 1.  ])
>>> data_cm = np.array([123, 223, 323, 423, 523])
>>> normalize(data_cm)
array([0.  , 0.25, 0.5 , 0.75, 1.  ])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 标准化

标准化是将数据转换为均值为0, 标准差为1的标准正态分布.
它是通过一组数据中的每个元素减去改组数据的均值并除以标准差来实现的.
标准化的目的是使得数据的分布接近标准正态分布, 这有助于许多机器学习算法的性能提升.

>>> import numpy as np
>>> def standardize(data):
        mean_val = np.mean(data)
        std_dev = np.std(data)
        standardized_data = (data - mean_val) / std_dev
        return standardized_data

>>> data_m = np.array([1, 2, 3, 4, 5])
>>> standardize(data_m)
array([-1.41421356, -0.70710678,  0.        ,  0.70710678,  1.41421356])
>>> data_cm = np.array([123, 223, 323, 423, 523])
>>> standardize(data_cm)
array([-1.41421356, -0.70710678,  0.        ,  0.70710678,  1.41421356])
1
2
3
4
5
6
7
8
9
10
11
12
13
统计学
pandas基本操作

← pandas基本操作→

最近更新
01
卷积神经网络
01-17
02
过拟合与欠拟合的处理
01-16
03
Mnist分类任务
01-16
更多文章>
Theme by Vdoing | Copyright © 2023-2025 DC | One Piece