 线性回归
线性回归
该系列的学习来自视频: https://space.bilibili.com/488051491/channel/collectiondetail?sid=2034514
先简单铺垫下一些常识:
- AI包含机器学习,机器学习包含深度学习
- 1)在没有深度学习之前,需要人为的进行特征的筛选、进行特征工程,然后再利用传统机器学习算法进行模型的构建
特别针对非结构化数据(视频、音频等),人为进行特征工程等处理是非常繁琐的!
2)有了深度学习后,可以有效的减少人为的那些操作,深度学习会自动发现特征之间的关系,进行有效特征的提取和目标算法的完成.
- 深度学习有个关键的概念 神经网络(ANN)
深度学习的神经网络模型有很多
- 卷积神经网络 CNN
- 循环神经网络 RNN
- 机器学习可划分为 有监督学习、无监督学习、半监督学习、强化学习, 换个角度,还可以划分出 集成学习、在线学习、迁移学习等
- 有监督学习 有标签 > 回归(预测连续值)、分类(预测离散值)
- 无监督学习 无标签 > 聚类算法
- 强化学习 > 封闭环境的奖惩机制 eg:无人驾驶
在线跑Jupyter Notebook的平台: Kaggle、Colab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15

在构建好模型以后, 需要导入损失函数来计算模型预测的误差.
最后通过梯度下降算法求损失函数的最小值, 得到模型的最优参数值!
y_hat = wx+b 代入x, 找到相应的w和b,模型就出来了; 用loss量化y和y_hat之间的差距; 用梯度下降算法找到最优的w和b.
# 机器学习简单分类
机器学习分为 有监督学习、无监督学习、强化学习
- 有监督与无监督的区别在于,有无标准答案,前者有后者没有
- 有监督学习分为 回归任务和分类任务.
- 回归与分类的区别在于, 分类是预测离散值;回归是预测连续值!
1
2
3
4
2
3
4
# 常见术语
特征、标签、样本、数据集、y害特(预测值)、y真实值、权重/参数/weights、参数b/偏差、损失函数
- chatgpt上上亿的参数指的就是 权重
- 求权重,这也是所有机器学习/深度学习的目标
1
2
3
2
3
# 线性回归模型函数

# MSE损失函数
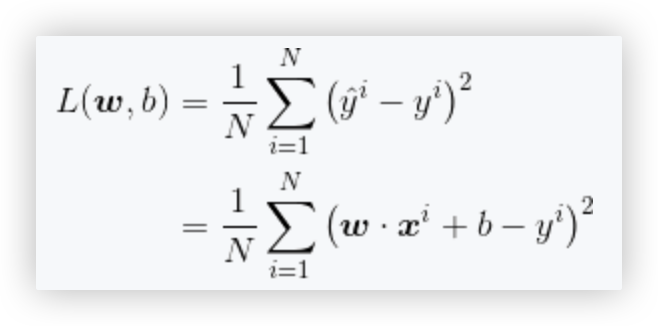
用多个样本的 预测值与真实值 之间的差值作为模型参数的优化依据!!
- 平方消除了负号的影响,求和则使用了多个样本,除以N 平均.
- MSE损失函数中,X特征矩阵、y标签值是已知的,所以自变量是w向量和b!! 求得w向量和b后,再将其带入线性回归模型函数中作后续的预测!!
1
2
3
2
3
用代码实现下:
import numpy as np
def mean_square_error(y, y_hat):
n = len(y)
loss = 0
for i, j in zip(y, y_hat):
loss += (i - j) ** 2
loss = (1 / n) * loss
return loss
# 模型预测值与样本标签值差距较大
y = [5.6, 9.6, 1.3]
y_hat = [2.5, 4.1, 5.8]
loss = mean_square_error(y, y_hat)
print(loss) # 20.03
# 模型预测值与样本标签值差距较小
y = [5.6, 9.6, 1.3]
y_hat = [5.2, 8.4, 0.9]
loss = mean_square_error(y, y_hat)
print(loss) # 0.58
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 梯度下降
初衷: 梯度下降算法就是说为了更新w和b的值,使得经过迭代后,w,b构建的网络预测的y_hat更贴近y..
在前面我们用MSE这个loss function描述了预测值与标签之间的差异, 那MSE损失函数中,什么样的 w向量和b 是最好的呢?
明确下我们的目标,我们像让 预测值与标签值越接近越好!!
那么就是求loss function越小时,w向量和b是多少!! -- 通过梯度下降来解决!
1
2
3
2
3

举个例子: y=x^2+1
y对x求导结果为2x,学习率为0.1
- x=-5 f‘(-5)=-10 x=-5-(-10)*0.1=-4
f(-5)=26 f(-4)=17 值减少了
- x=5 f‘(-5)=10 x=5-(10)*0.1=4
f(5)=26 f(4)=17 值减少了
1
2
3
4
5
6
7
2
3
4
5
6
7
用代码来简单实现下:
# 加载依赖库
import numpy as np
import matplotlib.pyplot as plt
# 定义 y=x^2+1 函数
def function(x):
y = x ** 2 + 1
return y
epochs = 50 # 指定自变量更新的次数(迭代的次数)
lr = 0.1 # 指定学习率的值
xi = -18 # 对自变量的值进行初始化
# 求取函数的梯度值
def get_gradient(x):
gradient = 2 * x
return gradient
trajectory = [] # 用于存储每次自变量更新后的值
# 利用梯度下降算法找到使得函数取最小值的自变量的值x_star
def get_x_star(xi):
for i in range(epochs):
trajectory.append(xi)
xi = xi - lr * get_gradient(xi) # ★!!★!!
x_star = xi
return x_star
get_x_star(xi) # 运行get_x_star函数 50次后x的值为-0.00025690458468707265
x = np.arange(-20, 20, 0.1)
y = function(x)
# 画出函数图像
plt.plot(x, y)
x_trajectory = np.array(trajectory)
y_trajectory = function(x_trajectory)
# 画图更新过程中的自变量与其对应的函数的值
plt.scatter(x_trajectory, y_trajectory)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
通过下图可以清楚的看到,斜率越大(越陡),步伐越大,往后,斜率小,步伐就小了,慢慢收敛,x自变量的值逐渐趋近于0,但不会等于0.
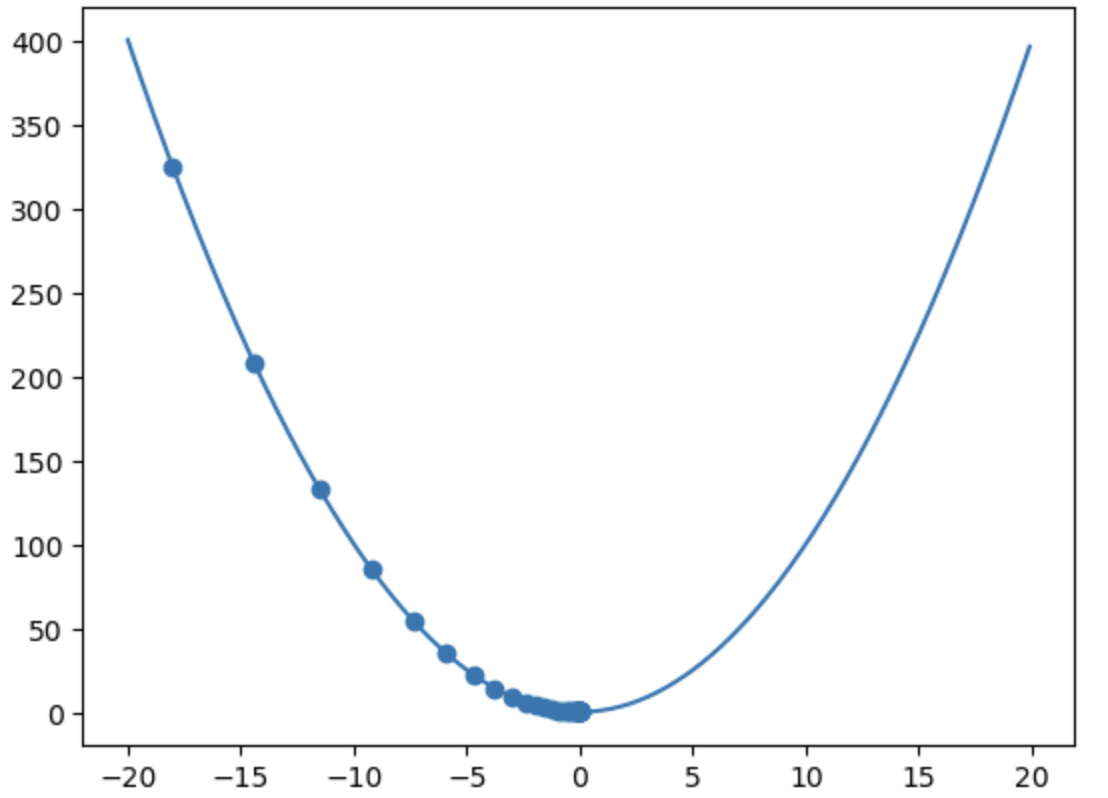
# 线性回归代码实战
第一步: 将 模型/线性回归函数 带入loss(w,b)损失函数中, 分别求loss对w和b的偏导..
第二步: 使用梯度下降算法更新模型参数 w = w - w的偏导*lr 、b = b - b的偏导*lr

# 准备数据集
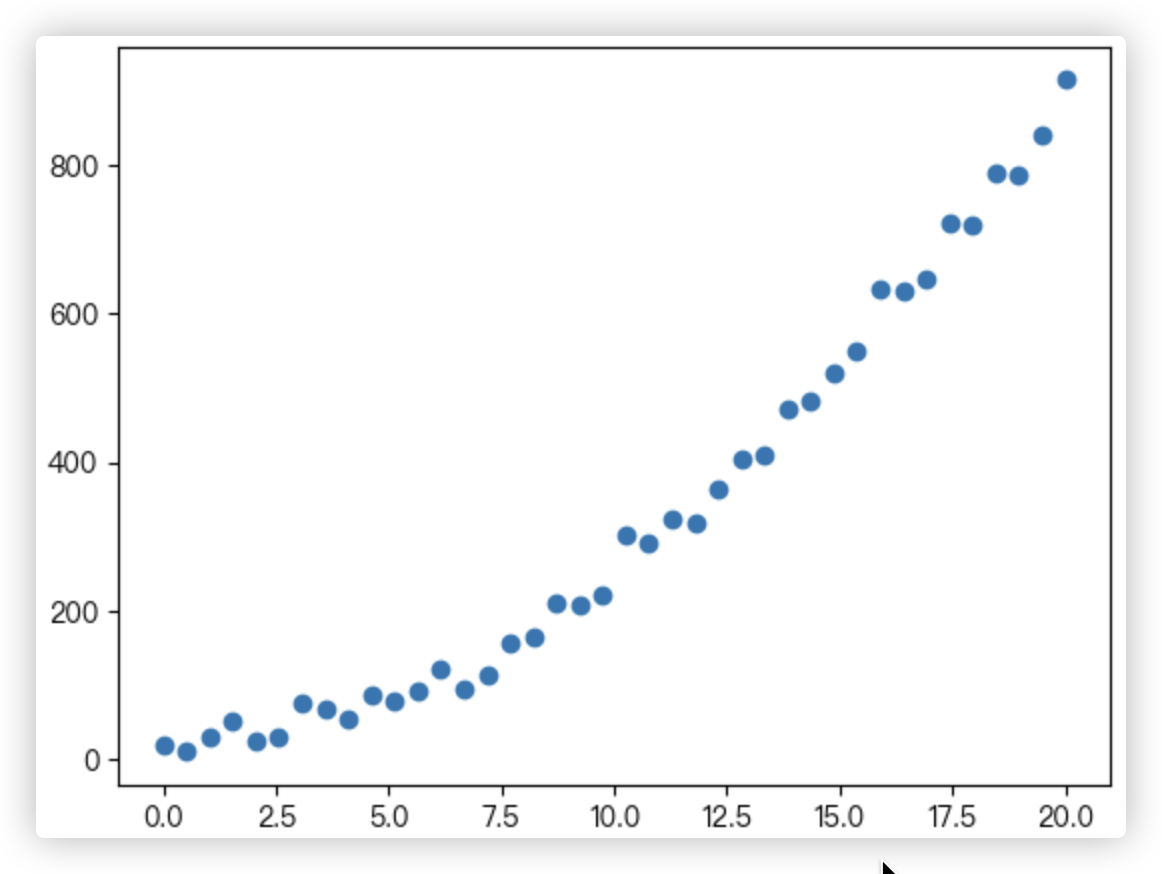
import pandas as pd
import numpy as np
# 加载数据集
dataset = pd.read_csv('dataset.csv') # 给csv文件只有两列,1个特征+1个标签,共40条数据
# 取出每个样本的特征
X = np.array(dataset['X'])
# 取出每个样本的标签
y = np.array(dataset['y'])
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['PingFang HK']
plt.rcParams['axes.unicode_minus'] = False # 避免坐标轴不能正常的显示负号
fig, ax = plt.subplots()
# 画出数据集中的样本
ax.scatter(X, y)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 数据集划分
# 训练集数据 前30条
X_train = X[0: 30]
y_train = y[0: 30]
n_train = len(X_train)
# 测试集数据 剩下的10条
X_test = X[30:]
y_test = y[30:]
n_test = len(X_test) # (30, 10)
# - 画出数据集分布和拟合的曲线
def plots(w, b, X, y):
fig, ax = plt.subplots()
# 画出数据集中的样本
ax.scatter(X, y)
# 画出线性回归模型的图像
ax.plot([i for i in range(0, 20)],
[model(i) for i in range(0, 20)])
plt.legend(('数据', '模型'),
loc='upper left',
prop={'size': 15})
plt.title("线性回归模型", fontsize=15)
plt.show()
# - 算MSE损失
def loss_funtion(X, y):
total_loss = 0
# 数据集中样本的个数
n_samples = len(X)
# 依次取出每一个数据中的每一个样本
for i in range(n_samples):
xi = X[i]
yi = y[i]
# 使用模型根据样本特征值进行预测
yi_hat = model(xi)
# 计算模型预测值与标签值之间的差距值
total_loss += (yi_hat - yi) ** 2
# 计算出对于给定数据集,模型预测的平均误差
avg_loss = (1 / n_samples) * total_loss
return avg_loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 简单回归 y=wx+b
w, b = -0.3, 0.6 # 把模型的参数w与b分别随机初始化为-0.3与0.6,后续不断迭代用梯度下降更新
lr = 0.001 # 指定学习率的值
# 构建线性回归模型
def model(x):
y_hat = w * x + b
return y_hat
epochs = 50000 # 指定模型使用梯度下降算法迭代更新参数的次数
for epoch in range(epochs):
# sum_w与sum_b用于存储计算梯度时相加的值
sum_w = 0.0
sum_b = 0.0
# - 求取参数w与b的梯度值
for i in range(n_train):
xi = X_train[i]
yi = y_train[i]
yi_hat = model(xi)
sum_w += (yi_hat - yi) * xi
sum_b += (yi_hat - yi)
grad_w = (2.0 / n_train) * sum_w # grad_w是参数w的梯度值
grad_b = (2.0 / n_train) * sum_b # grad_b是参数b的梯度值
# - 使用梯度下降算法更新模型参数
w = w - lr * grad_w
b = b - lr * grad_b
print(w,b) # 33.37314250522825 -54.75367322318991
train_loss = loss_funtion(X_train, y_train)
test_loss = loss_funtion(X_test, y_test)
print(train_loss,test_loss) # 1856.1190580180498 38350.64610218482
plots(w, b, X, y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
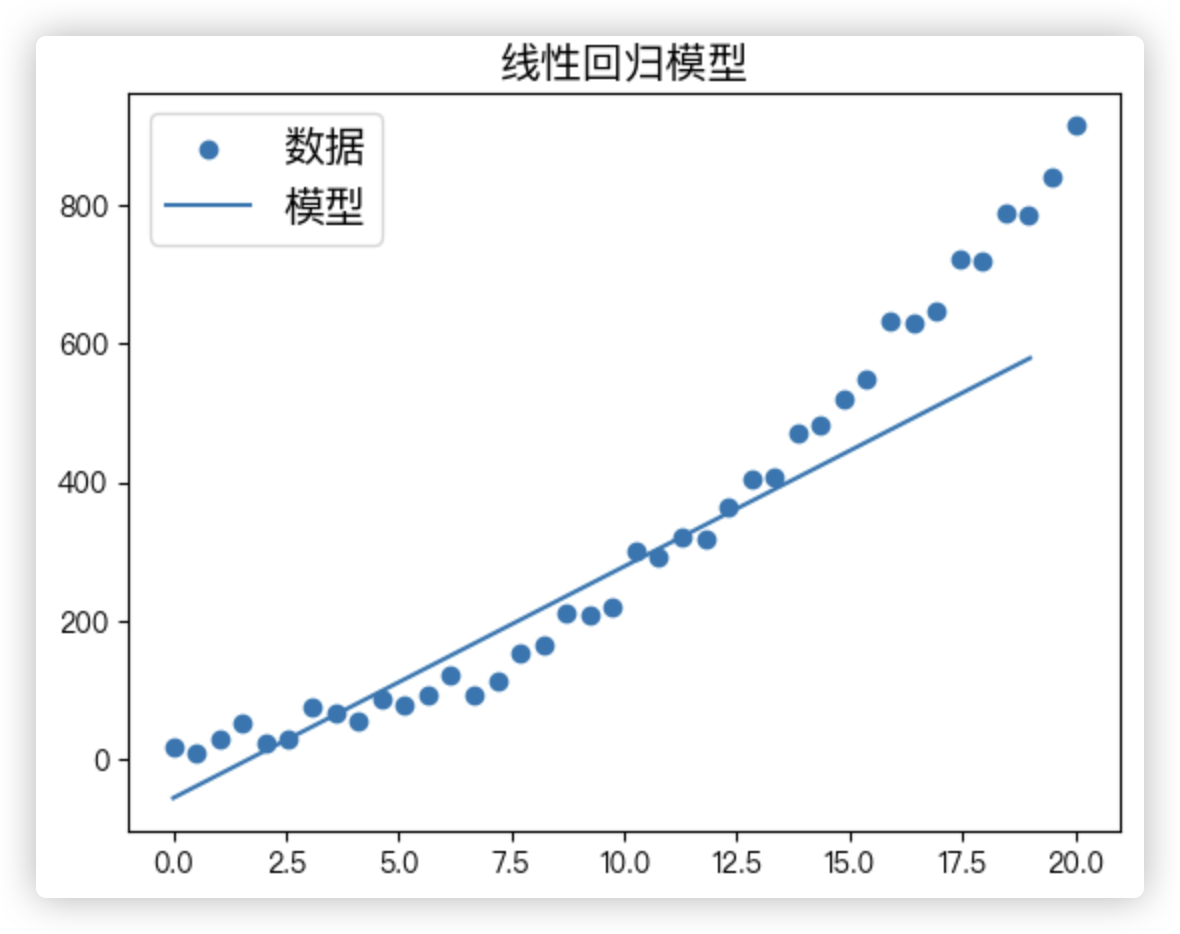
# 复杂回归 y=w1x1+w2x1^2 + b

用梯度下降更新w,b后, loss肯定是下降了的.. 不断迭代, loss不断下降. / 注意,每次迭代都会计算所有样本的损失..
w, b = np.random.rand(2), 1.1 # 把模型的参数w与b进行随机初始化
lr = 1e-6 # 指定学习率的值 1^10^-6
epochs = 5 # 指定模型使用梯度下降算法迭代更新参数的次数
# 构建复杂线性回归模型
def model(x):
y_hat = w[0]*x + w[1]*(x**2) + b
return y_hat
# 使用梯度下降算法更新模型参数
for epoch in range(epochs):
sum_w = np.zeros(2)
sum_b = 0.0
for i in range(n_train):
xi = X_train[i]
yi = y_train[i]
yi_hat = model(xi)
sum_w[0] += (yi_hat - yi) * xi
sum_w[1] += (yi_hat - yi) * (xi**2)
sum_b += (yi_hat - yi)
grad_w = (2.0 / n_train) * sum_w
grad_b = (2.0 / n_train) * sum_b
w = w - lr * grad_w
b = b - lr * grad_b
print(w,b) # [0.94880439 2.3415968 ] 1.120760858912231
train_loss = loss_funtion(X_train, y_train)
test_loss = loss_funtion(X_test, y_test)
print(train_loss,test_loss) # 459.9391188765701 1909.1676899729443
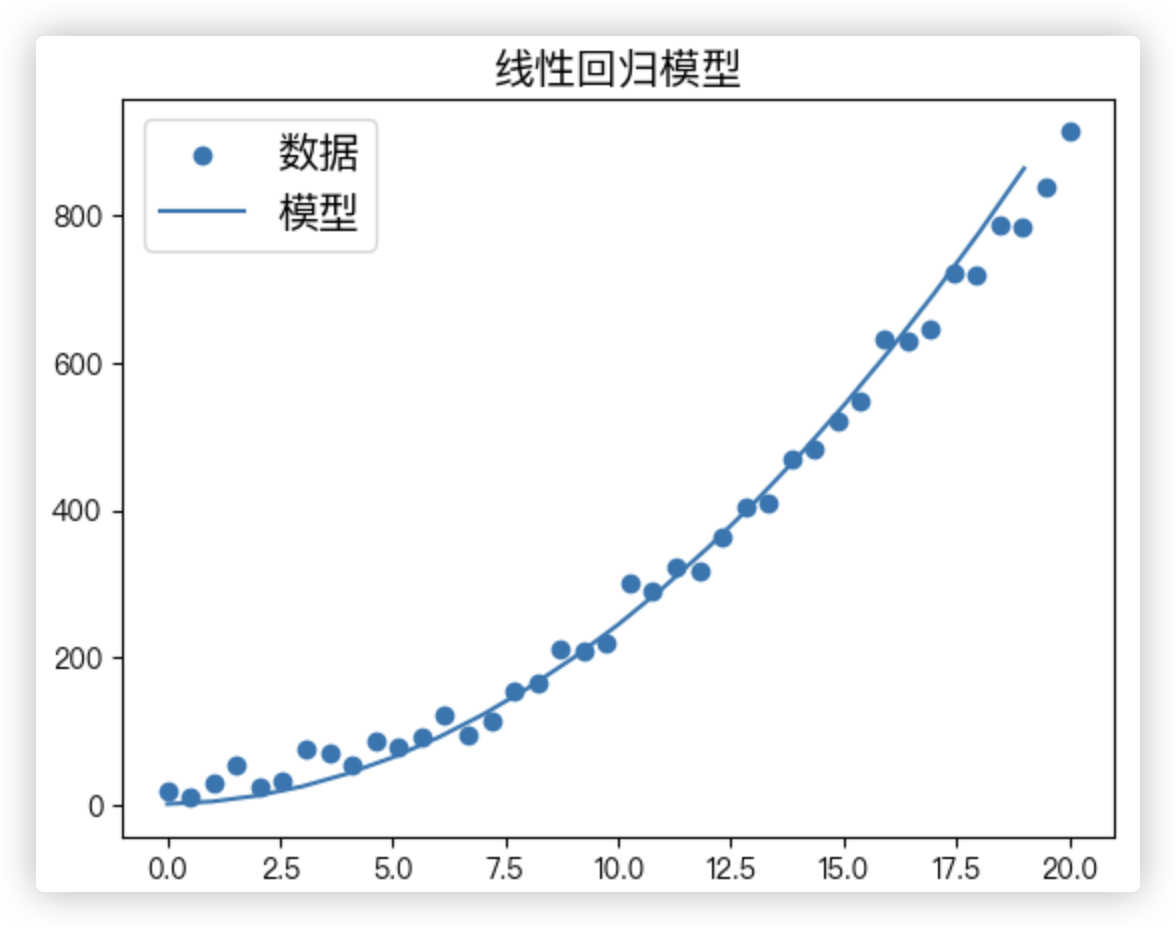
plots(w, b, X, y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 正则化 - 解决过拟合
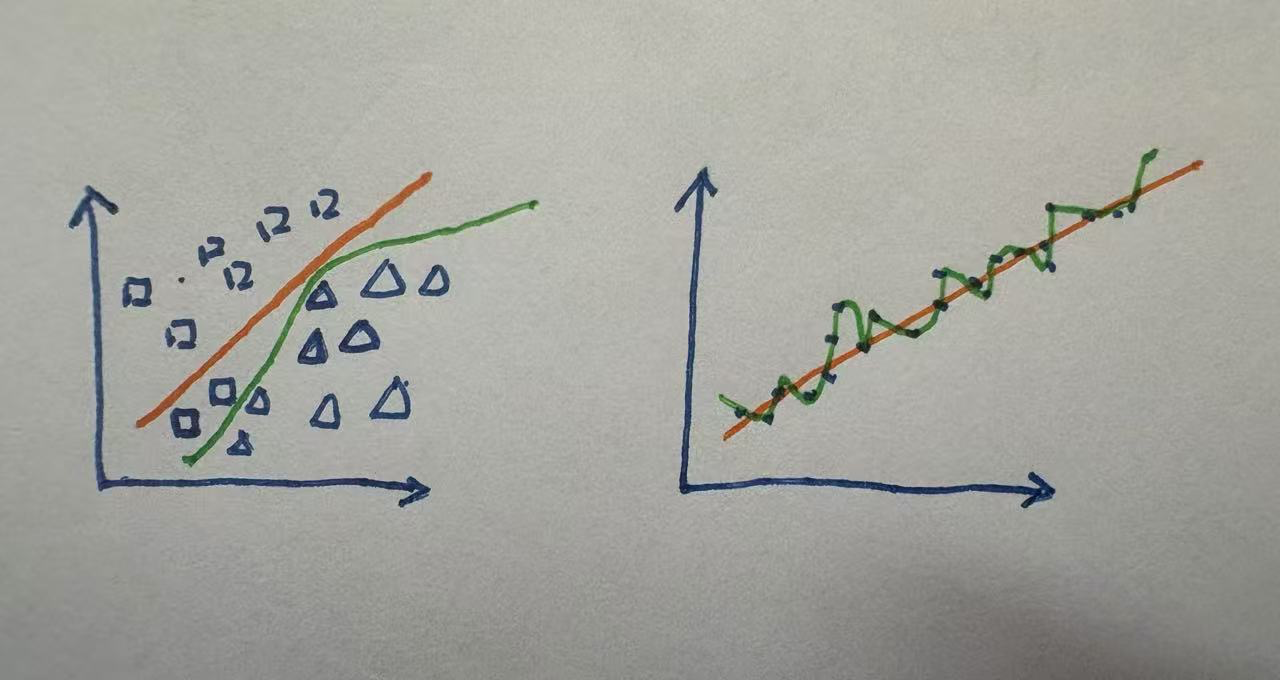
上图左侧是分类,右侧是回归.
橙色的线是正常的拟合,绿色的线是过拟合!!
- 以分类为例,橙色的线将两个正方形分到了三角形的区域;
绿色的线都分对了,虽然绿色的线使得我们的迭代目标train_loss小了,但是test_loss造成了极大的损失.
test_loss会比train_loss大很多!因为你不能保证这两个正方形不是 离异的/噪点/异常点!!
- 换个说法,过拟合考虑到了所有的细节,将不典型的特征当作了典型的特征来抓!
这就造成了后续测试的数据中,测试的数据没有这些不典型的特征,就容易分错! - 泛化能力差!
- 过拟合,在代码中的体现就是,train上表现还行,test表现不好!
> 在 线性回归代码实战 这一小节,简单回归和复杂回归
尽管代码中test_loss比train_loss大很多,但因为数据集的原因,画的图看起来还行!! 我们就不要纠结它了!
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
过拟合可以用正则化来解决. 什么是正则化呢?

上图中是L2正则化 里面的回归模型用的是上一小节的复杂回归 y=w1x1+w2x1^2+b
- 解决过拟合, loss损失函数 + 正则项
- 你这样想:
原先只有loss损失函数,梯度下降求最小损失的过程中,可不管W是多大,是多小,只有最后结果损失小就行.
但损失越小就越好吗?不见得,就像上面的那个我自己画的回归过拟合的图,拟合的线都经过每一个点了!!
So,损失太小了,会造成过拟合!!
加入正则项后,正则项肯定是一个正数,正则项成为了损失的一部分,要想损失小,就得让正则项小,就得让W小!!也就是不让loss中的w过大.
- 正则项分为L1 和 L2
L1 > λ 乘以 权重参数向量中每个w绝对值之和
目标: 将不重要特征的权重系数压缩到0,只保留下重要的特征,从而实现了特征选择.而重要特征对应的权重系数则会保留较大的值!
L2 > λ 乘以 权重参数向量中每个w的平方和
该惩罚项中的平方使得较大的权重系数被放大,从而产生更大的惩罚效果.
因此,它的目标: 通过降低所有特征的权重系数(而非只针对不重要特征),但一般不会被压缩到零
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
在代码中的体现. 同样是求偏导, 复杂回归小节的代码只需改动一行代码.
grad_w = (2.0 / n_train) * sum_w + (2.0 * reg * w)
1
# 波士顿房价 - 回归预测
其实跟前面的代码没啥区别,只是数据集不一样罢了.. 前面的数据是numpy,这里是DataFrame对象,取数据时有点不同.
"""
加载数据集
"""
import pandas as pd
dataset = pd.read_csv('boston_house_prices.csv',header=1,index_col=None)
X = dataset.iloc[:,:-1]
y = dataset['MEDV']
print(X.shape,y.shape) # (506, 13) (506,) X是DataFrame对象,y是Serise对象
"""
标准化,同一纲量 不然 x1 [100-10000] x2[0-1] 则对于预测值,x2这个特征可以忽略不计
"""
mean = X.mean(axis=0) # 求取数据集中所有样本特征值的均值 - 即每一列的均值
std = X.std(axis=0) # 求取数据集中所有样本特征值的方差 - 即每一列的方差
X = (X - mean) / std # 对数据集进行标准化
"""
数据集切分
"""
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
n_train = X_train.shape[0] # 训练集中样本的个数
n_features = X_train.shape[1] # 训练集中样本特征值的个数
n_train, n_features
"""
定义线性回归模型
"""
import numpy as np
w = np.random.rand(n_features) # 模型参数中的权重,随机初始化13个参数
b = 1.1 # 模型参数中的偏移项
def model(x):
y_hat = w.dot(x) + b # w.shape、x.shape都是(13,) w.dot(x)进行点乘操作, w0*x0+w1*x1+...+w12*x12
return y_hat
"""
求偏导,梯度下降更新参数
"""
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
lr = 0.001 # 指定学习率的值
epochs = 300 # 指定模型迭代训练的次数
reg = 0.5 # 指定正则项中lambda的值
# 使用梯度下降算法对模型进行迭代训练
for epoch in range(epochs):
sum_w = 0.0
sum_b = 0.0
for i in range(n_train):
xi = X_train.iloc[i] # 取第i行
yi = y_train[i] # 根据索引取每i个标签值. 因为y是Serise对象,So,上面需要将y标签的索引重新排列下!
yi_hat = model(xi)
sum_w += (yi_hat - yi) * xi
sum_b += (yi_hat - yi)
grad_w = (2.0 / n_train) * sum_w + (2.0 * reg * w) # 求梯度进行梯度下降,跟前面的代码并无不同,只是这里加了正则
grad_b = (2.0 / n_train) * sum_b
w = w - lr * grad_w
b = b - lr * grad_b
"""
算MSE损失
"""
def loss_funtion(X, y):
total_loss = 0
n_samples = len(X) # 数据集中样本的个数
# 依次取出每一个数据中的每一个样本
for i in range(n_samples):
xi = X.iloc[i]
yi = y[i]
yi_hat = model(xi) # 使用模型根据样本特征值进行预测
total_loss += (yi_hat - yi) ** 2 # 计算模型预测值与标签值之间的差距值
# 计算出对于给定数据集,模型预测的平均误差
avg_loss = (1 / n_samples) * total_loss
return avg_loss
train_loss = loss_funtion(X_train, y_train)
test_loss = loss_funtion(X_test, y_test)
print(train_loss,test_loss) # 169.65754430456232 181.95526760429433
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
