财务经营分析

该项目数据集链接: https://pan.baidu.com/s/1VVrAvcgJuxhxUFn7aKX_ow?pwd=3x34

针对2018-2022蜜雪冰城直营店和所有加盟店的财务报表数据. 基于该组数据进行"盈亏平衡"和"财务指标"分析.

1> '材料成本' + '直营店租金及运营费用' + '折旧与摊销费用' + '配送费用'
   + '销售与市场费用' + '一般管理费用' + '财务相关费用' == "总运营费用"
2> '产品销售收入' + '合作店收入' == '总收入'
3> '总收入' - "总运营费用" == '运营亏损'
4> '运营亏损' + '其它收支' == '净利润'

1
2
3
4
5

# 数据加载和预处理

df = pd.read_excel('./data/data.xlsx').T
df.columns = df.iloc[0]  # 将第一行作为数据的列索引
df = df.iloc[1:]  # 删除第一行数据
df

# df.info() # 发现数据全部为字符串类型
df = df.apply(lambda x:x.astype(int),axis=0)  # 将数据统一转换成数字类型
# 重新设置行索引
df.reset_index(drop=False,inplace=True)
df.rename(columns={'index':'年份'},inplace=True)
df.head(2)

1
2
3
4
5
6
7
8
9
10
11

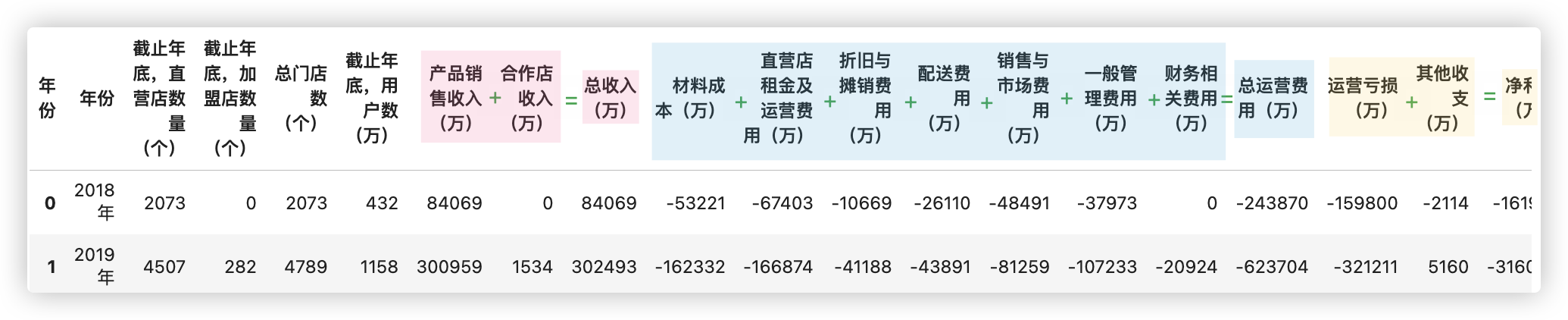
df.columns

"""
Index(['年份', '截止年底，直营店数量（个）', '截止年底，加盟店数量（个）', '总门店数（个）', '截止年底，用户数（万）',
       '产品销售收入（万）', '合作店收入（万）', '总收入（万）', '材料成本（万）', '直营店租金及运营费用（万）',
       '折旧与摊销费用（万）', '配送费用（万）', '销售与市场费用（万）', '一般管理费用（万）', '财务相关费用（万）',
       '总运营费用（万）', '运营亏损（万）', '其他收支（万）', '净利润（万）'],
       dtype='object', name='年份')
"""

1
2
3
4
5
6
7
8
9

# 盈亏平衡点分析

盈亏平衡点是企业总收入与总成本相等的点, 意味着在此点上企业既不盈利也不亏损.

# - 计算固定成本（使用绝对值）
df['固定成本（万）'] = (
    abs(df['直营店租金及运营费用（万）']) +
    abs(df['折旧与摊销费用（万）']) +
    abs(df['一般管理费用（万）']) +
    abs(df['财务相关费用（万）'])
)

# - 计算可变成本（使用绝对值）
df['可变成本（万）'] = abs(df['材料成本（万）']) + abs(df['配送费用（万）']) + abs(df['销售与市场费用（万）'])

# - 计算贡献毛利率: 单位贡献毛利(单位售价−单位可变成本) /单位售价
unit_selling_price = 10  # 假设每杯奶茶的平均售价（元）即单位售价
unit_variable_cost = 4   # 假设每杯奶茶的平均可变成本（元）即单位可变成本
df['贡献毛利率'] = (unit_selling_price - unit_variable_cost) / unit_selling_price

# - 计算盈亏平衡点（收入）: 固定成本 / 贡献毛利率
df['盈亏平衡点（收入，万）'] = df['固定成本（万）'] / df['贡献毛利率']

# 查看结果
df[['年份', '总收入（万）', '盈亏平衡点（收入，万）','贡献毛利率']]
# 画折线图
px.line(df,x='年份',y=['总收入（万）',"盈亏平衡点（收入，万）"],markers=True)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

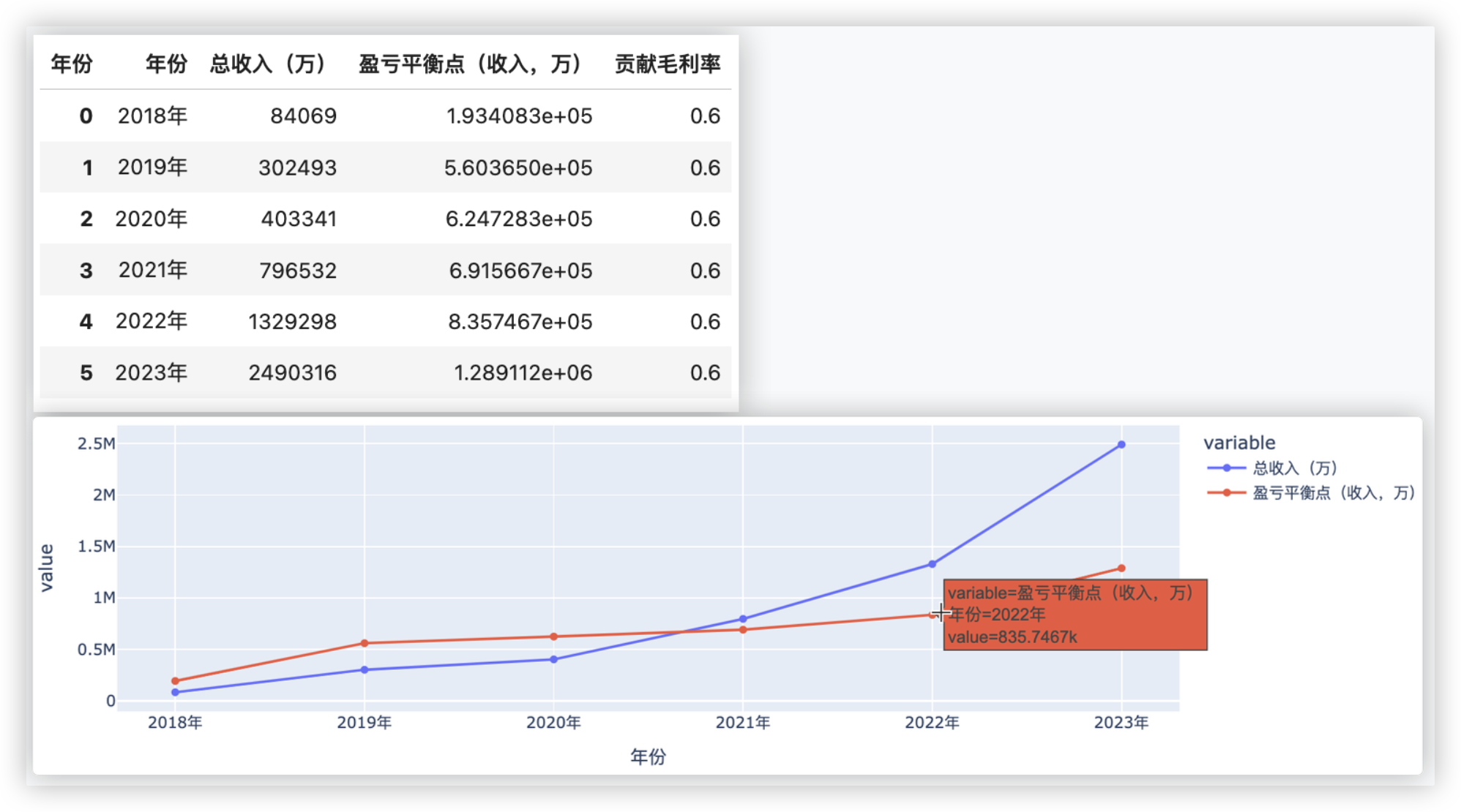
可以看到, 从2021年开始, 盈亏平衡点与收入开始相等(交叉).
之后的年份中, 总收入大幅超过盈亏平衡点的收入, 说明此时收入完全可以覆盖成本. 即2021年后, 企业起死回生.

# 每年的收入变化

# 直营店<即产品销售收入>和合作门店的收入变化
px.line(df,x='年份',y=['产品销售收入（万）',"合作店收入（万）"],markers=True)

1
2

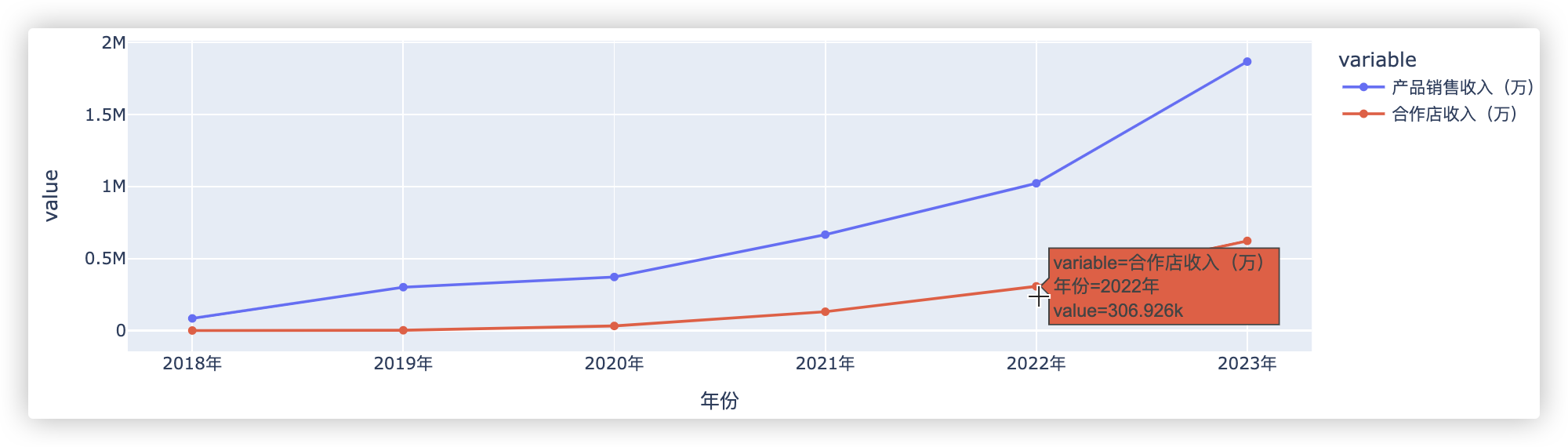
通过以上图表可以看出, 该企业自2018年后, 直营店销售收入和合作店收入均呈现线性增加.

# 直营店和合作门店的收入占比 注:直营店收入+合作门店收入=总收入
# - 计算各项成本占比,并格式化为两位小数
t = pd.DataFrame()
t['年份'] = df['年份']
t["产品销售收入占比"] = (df['产品销售收入（万）'] / df['总收入（万）'] * 100).round(2)
t["合作店收入占比"] = (df['合作店收入（万）'] / df['总收入（万）'] * 100).round(2)
t

# - 堆叠条形图
px.bar(t,x='年份',y=['产品销售收入占比','合作店收入占比'])

1
2
3
4
5
6
7
8
9
10

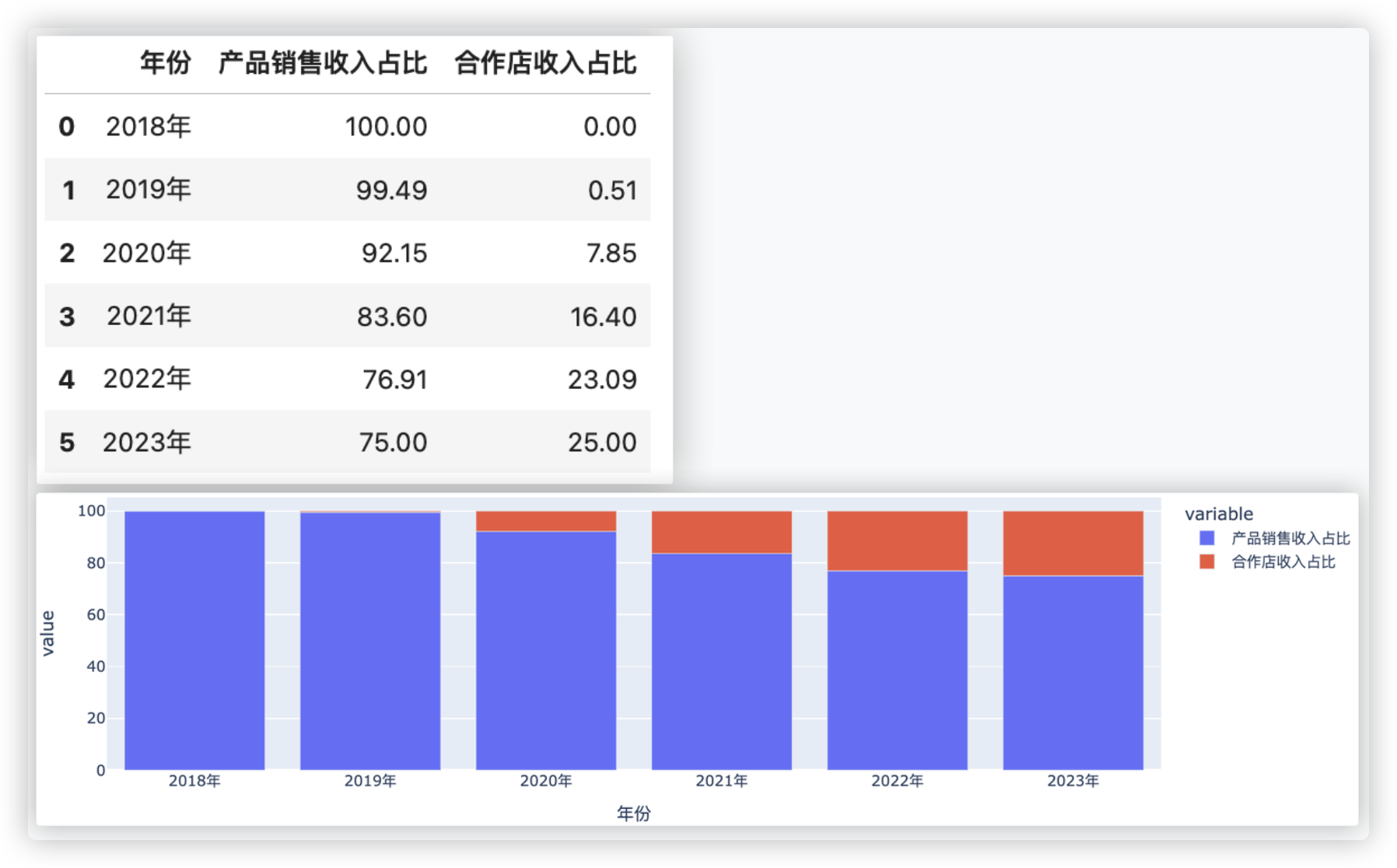
通过上面的条形图可以看出, 该企业自2018年后, 直营店收入占比有减少, 合作门店收入占比逐年增加.
通过直营店和合作门店相关的条形图和折线图可以看出:
-1- 企业整体业务在扩展, 市场需求在增长.(直营店和合作店收入的线性增长).
-2- 合作店收入的增加也反映了品牌影响力的增强, 更多的合作伙伴愿意加入, 说明品牌在市场上的认可度和美誉度较高.

# 每年的成本变化

# - 各项成本变化
item = ['材料成本（万）','直营店租金及运营费用（万）','折旧与摊销费用（万）','配送费用（万）',
        '销售与市场费用（万）','一般管理费用（万）','财务相关费用（万）']
# 这里的各项支出在表格里都是负数,偶尔有一个是正数,为了画图有更高的展示效果,都乘以`-1`
df = df.apply(lambda x:x * -1 if x.name in item else x,axis=0)
df
px.line(df,x='年份',y=item,markers=True)

1
2
3
4
5
6
7

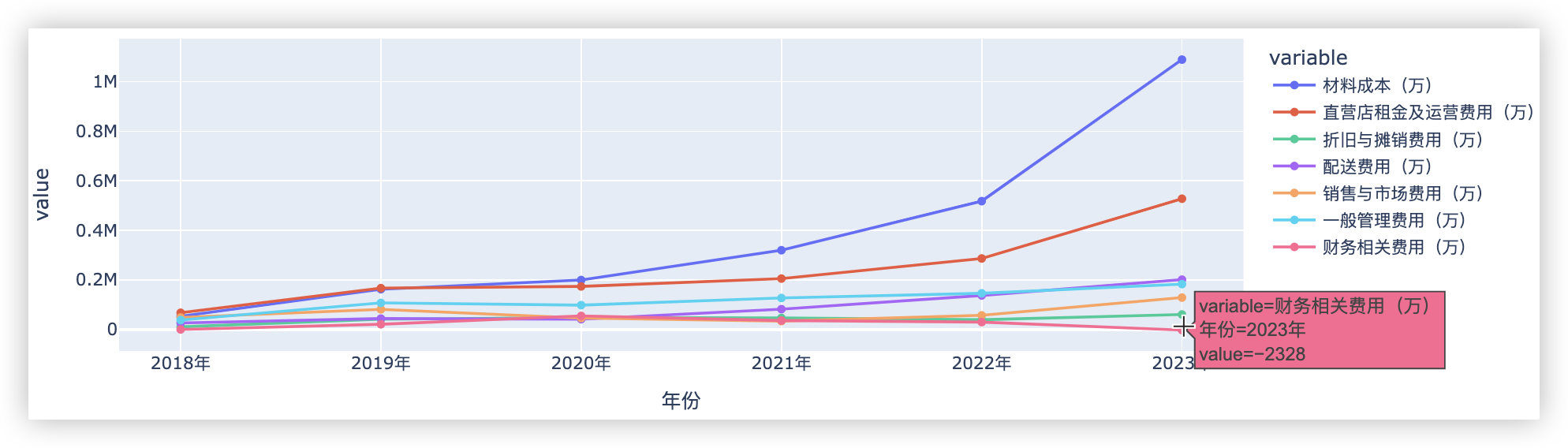
通过以上图表, 可以看出:
该企业的材料成本、直营店租金及运营费用大幅度增加, 配送费用、销售与市场费用、一般管理费用也有所增加

df_cb=pd.DataFrame()
df_cb['年份'] = df['年份']
# ps:你观察表格,偶尔有项支出是正数.所以,是乘以`-1`,而不是abs取绝对值. 画堆叠图,就是正的部分+负的部分等于1.
df['总运营费用（万）'] = df['总运营费用（万）'] * -1
# 计算各项成本占比
df_cb['材料成本占比'] =(df['材料成本（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['直营店租金及运营费用占比'] =(df['直营店租金及运营费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['折旧与摊销费用占比'] =(df['折旧与摊销费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['配送费用占比'] =(df['配送费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['销售与市场费用占比'] =(df['销售与市场费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['一般管理费用占比'] =(df['一般管理费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb['财务相关费用占比'] =(df['财务相关费用（万）'] /df['总运营费用（万）'] * 100).round(2)
df_cb

# 堆叠条形图
px.bar(df_cb,x='年份',y=['材料成本占比','直营店租金及运营费用占比','折旧与摊销费用占比',
                        '配送费用占比','销售与市场费用占比','一般管理费用占比','财务相关费用占比'])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

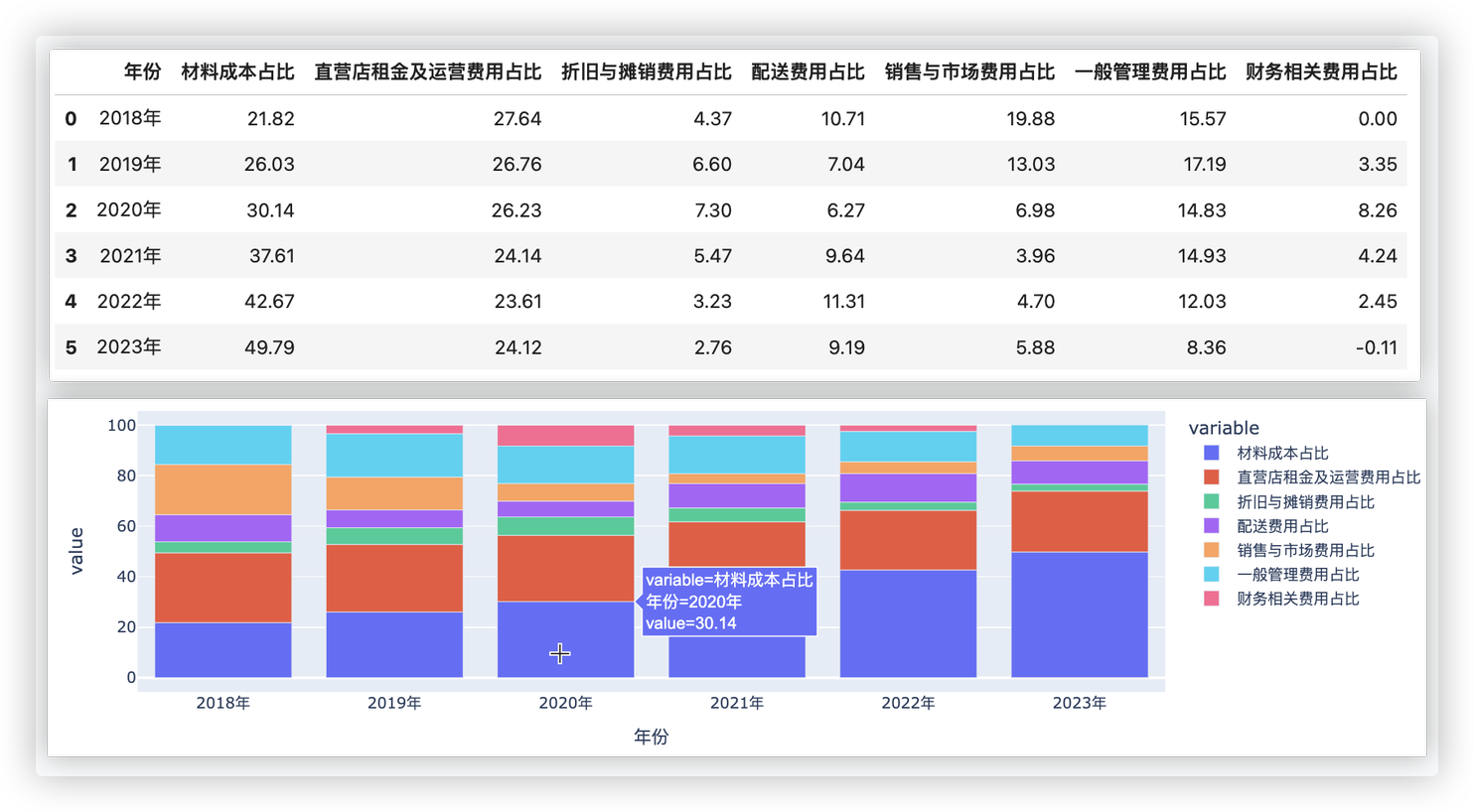
该企业的材料成本、直营店租金及运营费用大幅度增加,配送费用、销售与市场费用、一般管理费用也有所增加.
但其中只有材料成本占比逐年增加, 直营店租金及运营费用、配送费用基本不变,
销售与市场费用、一般管理费用占比逐渐减小, 说明:

材料成本的增长速度快于其他费用的增长速度. 原材料价格的上涨或企业对高质量原材料的依赖增加,对于奶茶品质追求有所提升.
直营店租金及运营费用的绝对值增加, 但其占比基本不变, 表明这些费用的增长与企业总收入的增长基本同步,
企业在租金和运营方面的成本控制较为稳定。
配送费用的绝对值增加, 但占比基本不变说明企业在扩展业务的同时, 配送效率有所提升, 配送成本的增长与业务扩展的速度相匹配。
尽管销售与市场费用、一般管理费用有所增加, 但其占比逐渐减小, 表明企业在这些方面的费用控制较为有效, 可能通过优化管理和市场策略, 提高了费用使用的效率。

综上所述,该奶茶企业在材料成本上面临较大压力,但在租金、运营、配送、销售与市场、一般管理费用方面的成本控制较为有效,
显示出企业在扩展业务的同时,能够较好地管理和优化各项费用。

# 财务指标-盈利能力分析

盈利能力分析是财务分析的重要组成部分, 它涉及评估公司赚取利润的能力.
计算盈利指标: 利用财务报表中的数据计算各种盈利指标.
包括但不限于, 利率、净利率、利息保障倍数、收入增长率、利润增长率等指标.

# 1. 计算毛利率 = （总收入 - 材料成本）/ 总收入
#    >> 毛利率衡量的是公司销售收入中用于支付材料成本的比例,是衡量公司产品定价能力和成本控制的指标
df['毛利率'] = (df['总收入（万）'] - df['材料成本（万）']) / df['总收入（万）']

# 2. 计算净利率 =  净利润 / 总收入
#    >> 净利率反映了公司在扣除所有成本和费用后所保留的利润率.
df['净利率'] = df['净利润（万）'] / df['总收入（万）']

# 3. 计算利息保障倍数 = 营业利润 / 财务相关费用. 除数不可为0,因此将[财务相关费用]中的0替换成1
#    营业利润 = 总收入 - 材料成本 - 总运营费用
#    >> 利息保障倍数是指公司支付利息的能力,即营业利润是否足以支付利息费用。
df['营业利润'] = df['总收入（万）'] - df['材料成本（万）'] - df['总运营费用（万）']
df['利息保障倍数'] = df['营业利润'] / (df['财务相关费用（万）'].replace({0: 1}))

# 4. 计算收入增长率 = 当前总收入与前一个总收入之间的百分比变化
#    >> 收入增长率反映了公司收入增长的速度和趋势
df['收入增长率'] = df['总收入（万）'].pct_change()

# 5. 计算利润增长率 = 当前净利润与前一个净利润之间的百分比变化
#    >> 利润增长率反映公司净利润的增长速度
df['利润增长率'] = df['净利润（万）'].pct_change()

# 查看结果
df[['年份', '毛利率', '净利率', '利息保障倍数', '收入增长率', '利润增长率']]


# 不同年份对应的财务指标可视化
# 创建子图
fig, axs = plt.subplots(3, 2, figsize=(14, 12))

# 绘制毛利率
axs[0, 0].plot(df['年份'], df['毛利率'], marker='o', label='毛利率')
axs[0, 0].set_title('毛利率趋势')
axs[0, 0].set_xlabel('年份')
axs[0, 0].set_ylabel('毛利率')

# 绘制净利率
axs[0, 1].plot(df['年份'], df['净利率'], marker='o', color='orange', label='净利率')
axs[0, 1].set_title('净利率趋势')
axs[0, 1].set_xlabel('年份')
axs[0, 1].set_ylabel('净利率')

# 绘制利息保障倍数
axs[1, 0].plot(df['年份'], df['利息保障倍数'], marker='o', color='green', label='利息保障倍数')
axs[1, 0].set_title('利息保障倍数趋势')
axs[1, 0].set_xlabel('年份')
axs[1, 0].set_ylabel('利息保障倍数')

# 绘制收入增长率
axs[1, 1].plot(df['年份'], df['收入增长率'], marker='o', color='red', label='收入增长率')
axs[1, 1].set_title('收入增长率趋势')
axs[1, 1].set_xlabel('年份')
axs[1, 1].set_ylabel('收入增长率')

# 绘制利润增长率
axs[2, 0].plot(df['年份'], df['利润增长率'], marker='o', color='purple', label='利润增长率')
axs[2, 0].set_title('利润增长率趋势')
axs[2, 0].set_xlabel('年份')
axs[2, 0].set_ylabel('利润增长率')

# 移除空子图
fig.delaxes(axs[2, 1])

plt.tight_layout() #防止子图之间的重叠和标签被截断
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

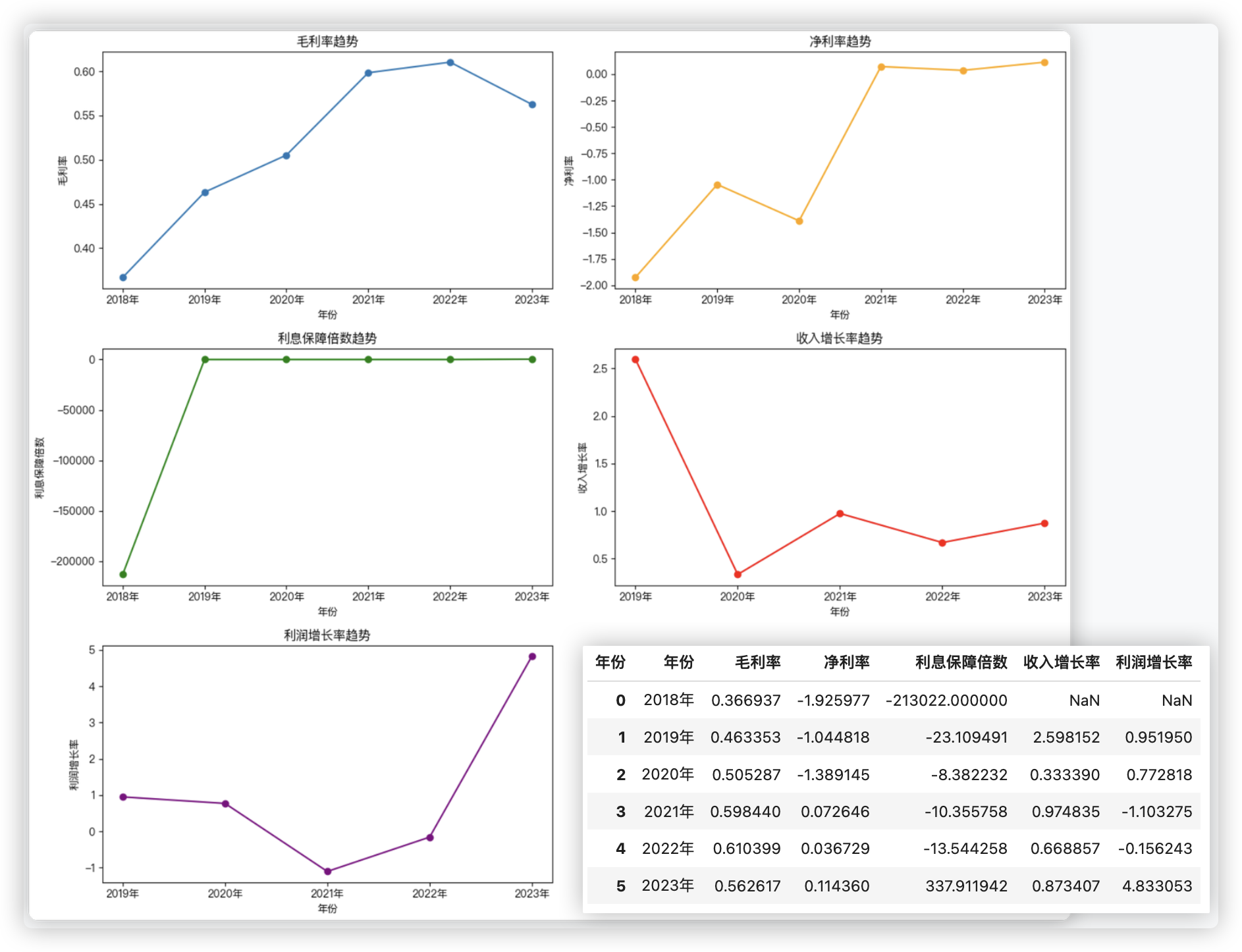
- 毛利率分析:毛利率衡量的是公司销售收入中用于支付材料成本的比例,是衡量公司产品定价能力和成本控制的指标。
    - 2018年-2023年:毛利率逐年上升,表明企业在成本控制和产品定价方面有显著改善。
    - 2022年达到峰值:在2022年毛利率达到最高（0.61）,随后略有下降,可能受到材料成本上涨或市场竞争加剧影响。

- 净利率分析:净利率反映了公司在扣除所有成本和费用后所保留的利润率。
    - 2018年-2020年:净利率为负,表明公司处于亏损状态。
    - 2021年-2023年:净利率转正,并在2023年达到0.114,表明公司实现盈利,整体财务状况显著改善。
      
- 利息保障倍数:是指公司支付利息的能力,即营业利润是否足以支付利息费用。
    - 2018年:利息保障倍数为负,意味着公司在营业利润无法覆盖利息费用。
    - 2019年-2022年:该比率逐年改善,2022年达到13.54,显示公司有更强的偿债能力。
      
- 收入增长率:收入增长率反映了公司收入增长的速度和趋势。
    - 2018-2019年:显著增长2.6倍,表明市场扩张和销售策略见效。
    - 2021年:增长率接近翻倍（0.974）,显示出极强的市场接受度。
    - 2023年:继续保持高增长（0.873）,但增速略微放缓
      
- 利润增长率:反映公司净利润的增长速度。
    - 2018年-2020年:净利润有浮动增长（见净利润图）,但利润率为负表示仍未实现盈利。
    - 2021年:由于净利率转正（见净利润图）,利润增长率为负，表明公司已扭亏为盈。
    - 2023年:利润增长大幅提升，达到4.83,表明盈利能力极大改善。
      
- 总结:
    - 成本与定价:公司在成本控制和产品定价上取得了明显的进步,尤其是在2021年及以后。
    - 盈利能力:公司的净利润已转正,并在2023年达到显著增长,这表明经营战略的成功。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 用户潜力分析

用户数量增长与哪些指标有关?

#提取与用户增长有相关关联的字段
columns_of_interest = [
    '截止年底，直营店数量（个）', '截止年底，加盟店数量（个）', '总门店数（个）', '截止年底，用户数（万）',
    '产品销售收入（万）', '合作店收入（万）', '总收入（万）', '材料成本（万）', '直营店租金及运营费用（万）',
    '折旧与摊销费用（万）', '配送费用（万）', '销售与市场费用（万）', '一般管理费用（万）', '财务相关费用（万）', '其他收支（万）'
]

# 绘制热力图, 查看 [用户数] 和其他相关字段的相关系数
# 选择包含这些列的数据子集
df_filtered = df[columns_of_interest]

# 计算相关性矩阵
correlation_matrix = df_filtered.corr()

# 可视化相关性矩阵
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5)
plt.title('Correlation Matrix')
plt.show()

# 探究与用户增长（截止年底用户数）的相关性
user_growth_correlation = correlation_matrix['截止年底，用户数（万）'].sort_values(ascending=False)
print(user_growth_correlation)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

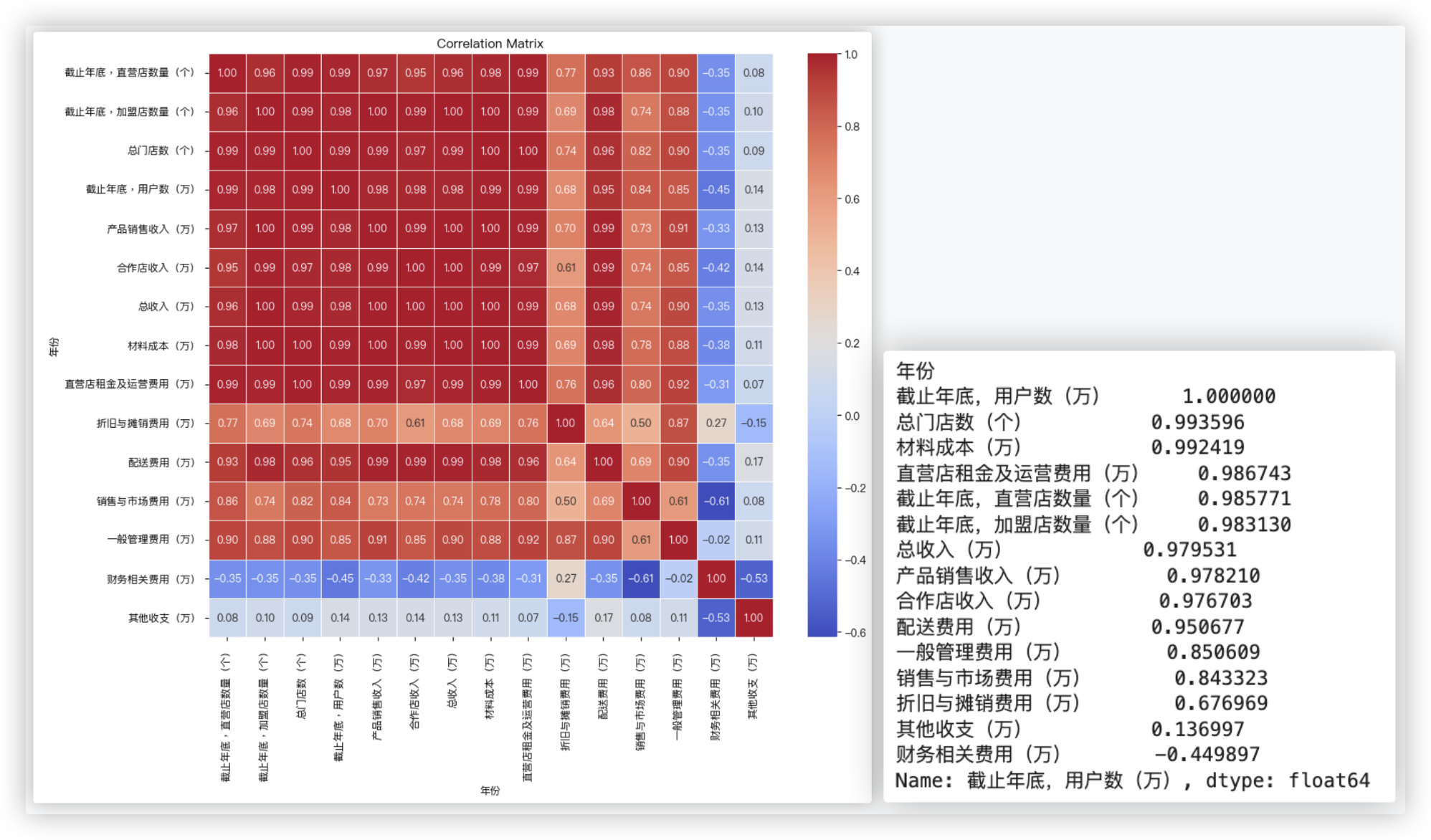
总门店数（个） 和 材料成本（万） 与用户增长的相关性非常高。这表明:

1. 用户数量的增长和总门店数的增加反映了企业在运营效率方面的提升。
   通过优化供应链管理和提高生产效率,能够更好地应对材料成本的上升,满足用户需求。
2. 随着用户数量的增加,企业需要更多的原材料来生产足够的产品以满足需求。
   但企业可以通过大规模采购原材料来获得更优惠的价格,从而部分抵消材料成本的上升。

直营店租金及运营费用（万） 和 截止年底,直营店数量（个） 也有很高的相关性,说明直营店的数量和其相关费用对用户增长有显著影响。
总收入（万） 和 产品销售收入（万） 等与收入相关的指标也与用户增长相关性较高。
其他收支（万） 和 财务相关费用（万） 的相关性为负值。这表明这些因素与用户增长可能有负向关系。

1
2
3
4
5
6
7
8
9
10

← 连锁超市数据分析拍拍贷数据分析→