 ★特征工程+线性回归
★特征工程+线性回归
切记, 不要纠结于 实现原理中涉及到的数学公式.. 只需要知道它是做什么的, 用代码如何实现即可!! (´・Д・)」
# 机器学习是什么?
先来理解人工智能:
- 人工智能只是一个抽象概念, 它不是任何具体的机器或算法. 它可以对人的意识、思维进行模拟, 但又不是人的智能.
- 计算速度: 象棋能看几十步远
算法: 围棋用暴力求解太浪费算力了
识别规则: 猫>有两只三角形耳朵, 圆脸.. 蜷缩着,躲被子里呢?
★ 由于人们没有办法设计出足够复杂的规则来精确描述世界
So, AI 系统需要具备自我学习的能力, 即从原始数据中获取有用的知识. 这种能力被称为机器学习
★ 机器学习可以利用 [已有的数据] 进行 [学习] , 获得一个训练好的 [模型]/类似于人类的经验, 然后可以利用此模型 [预测] 未来的情况.
2
3
4
5
6
7
8
9
10
# 机器学习常用的概念
□
楼层、面积、采光率 --决定-- 售价
- 特征数据/自变量/一个样本的描述信息 : 楼层、面积、采光率
- 标签数据/因变量/一个样本数据的结果 : 售价
□
有监督类别: 用到的样本需要传特征和标签.
无监督类别: 用到的样本只需传特征..不需要标签..
2
3
4
5
6
7
8
# 数据集切分
◎ sklearn提供的开源数据集
from sklearn import datasets as ds
wine = ds.load_wine # 红酒数据集,它是一个二维的数组,看作是一个excel表格就行!
wine.shape # (178,13)
wine.data # 特征
wine.target # 标签
◎ 数据集切分
将一组数据进行二八分, 80%的数据用于训练, 20%的数据用于对训练的结果进行测试
from sklearn.model_selection import train_test_split
# 训练特征,测试特征,训练标签,测试标签 = train_test_split(特征,标签,测试集占比,打乱的随机种子)
train_x,test_x,train_y,test_y = train_test_split(wine.data,wine.target,0.2,2060)
"""
stratify = y 一般用在分类场景上 确保 切分后 y_train 以及 y_test 中的 0 和 1 的比例与切分前 y 中的比例一致
(假如数据集标签的类别只有两类 用0和1表示)
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
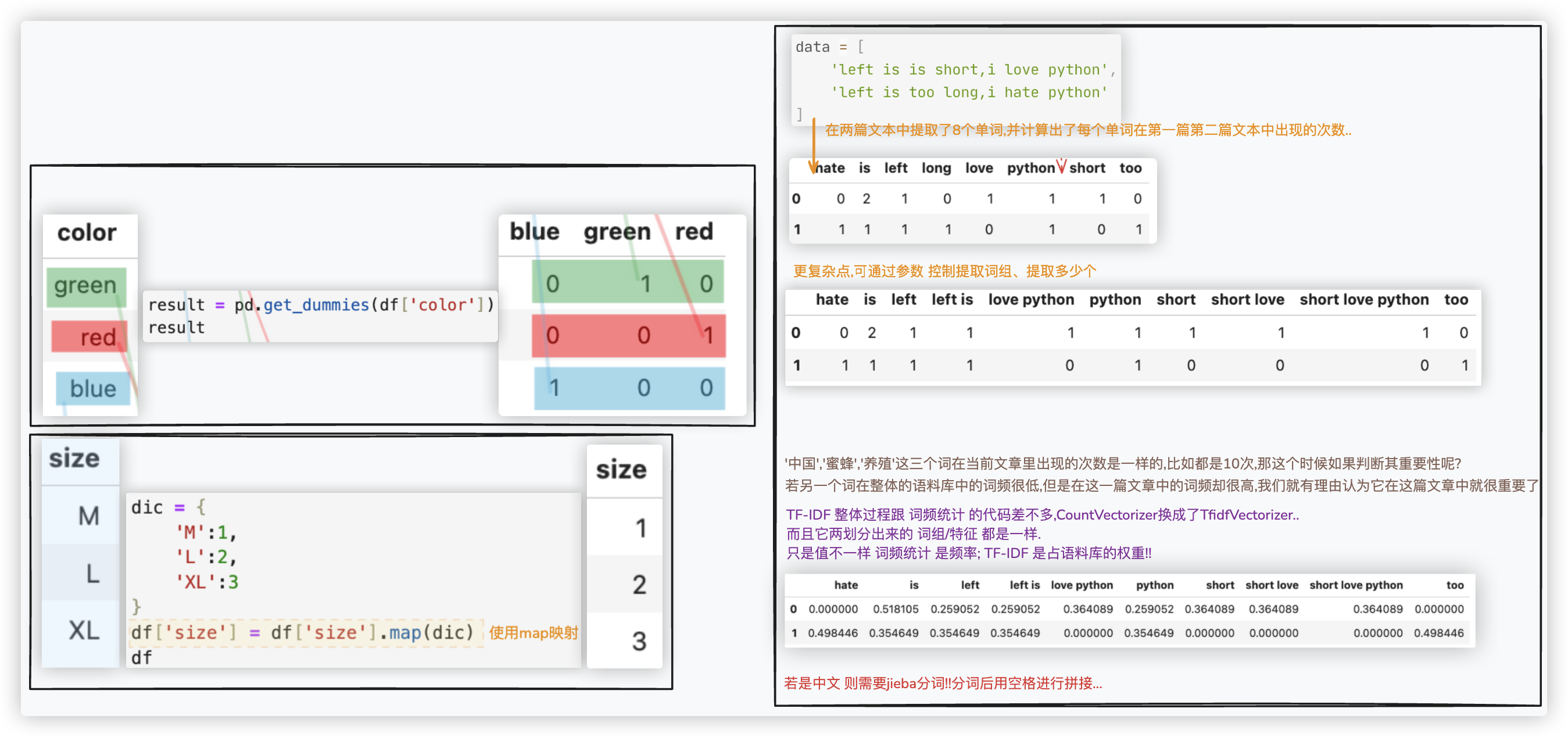
# 特征工程 - 特征抽取
- 独热编码
result = pd.get_dummies(df['color'])
df = pd.concat((df,result),axis=1).drop(columns='color')
- 标签编码
dic = {
'M':1,
'L':2,
'XL':3
}
df['size'] = df['size'].map(dic)
- 文本向量化
两个方案: 基于-词频 & 基于-权重!! >> 两个方案都是
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
tool = 类(一些参数设置) # 类实例化 eg: tool = TfidfVectorizer(ngram_range=(1,2),max_features=10)
# !! maybe to do: 若是中文,那么data需要先jieba分词后用空格进行拼接
res = tool.fit_transform(data).toarray() # 将一列特征数据拿给机器学习处理,得到特征矩阵,toarray转换为数组,二维的!!
feature_names = tool.get_feature_names_out() # 获取到文本向量化的结果!!/得到文本拆分出的一堆列名
df = pd.DataFrame(data=res,columns=feature_names)
df
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 特征工程 - 特征无量纲化
# from sklearn.preprocessing import MinMaxScaler # 归一化
from sklearn.preprocessing import StandardScaler # 标准化
import numpy as np
import pandas as pd
data = pd.DataFrame(data=np.random.randint(0,100000,size=(5,3)))
# tool = MinMaxScaler()
tool = StandardScaler()
res_data = tool.fit_transform(data)
"""☆ 补充,若先对数据集进行了二八分.
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
# fit后,均值、标准差等信息都保存到了standard_scaler这个对象中!!
standard_scaler.fit(X_train)
# 查看每一列的均值和标准差
standard_scaler.mean_,standard_scaler.scale_
# 训练集特征开始归一化!!
X_train_standard = standard_scaler.transform(X_train)
# ★★★★ 测试集特征的归一化,应使用训练集特征归一化得到的均值和标准差!!
# - 若你重新对测试集特征归一化,使用测试集特征的test_mean和test_standard,就掉进陷阱里的了
# 因为测试集模拟的是真实环境,在该环境中是很难得到均值和标准差的!! (PS 特征数/列数 都一样.)
X_test_standard = standard_scaler.transform(X_test)
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 特征工程 - 特征选择
# 方差过滤
import numpy as np
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
# 创建数据集
df = pd.DataFrame(data=np.random.randint(1,50,size=(10,8)))
df
#方差过滤
tool = VarianceThreshold(threshold=200) # 创建工具对象,参数threshold是阀值,表示过滤掉方差低于该值的特征列
"""
ret = tool.fit_transform(df) 内部执行了两步
Step1: 对数据集中的每个特征计算方差.
Step2: 根据设定的阈值,选择方差大于阈值的特征作为重要特征.
"""
ret = tool.fit_transform(df) # 根据指定的阈值threshold过滤低于阈值的特征
print(ret)
# 后续To do: 使用选定的重要特征ret 进行模型训练和评估.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# PCA降维
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
iris = datasets.load_iris() # 将鸢尾花作为样本数据
X = iris.data
y = iris.target
# 另一种写法: pca_line = PCA() ret=pca_line.fit_transform(X)
pca_line = PCA().fit(X) # PCA不写参数n_components,则所有特征都保留
ret = pca_line.transform(X) # 特征降维操作 尽管这里原始数据4个特征,PCA降维保留的也是4个特征,但数据肯定是不一样的了!!
# pca_line.explained_variance_ # 每一列可解释方差大小
# 每一列可解释方差贡献率
# 即 查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比
# 它 等同于 np.var(ret,axis=0) / np.var(X,axis=0).sum()
# 它 等同于 pca_line.explained_variance_ / pca_line.explained_variance_.sum()
var_rate = pca_line.explained_variance_ratio_
# 画图 求PCA的n_components参数的最优解,评判指标:尽可能多的保留原始数据的信息
n_components_list = list(range(1,X.shape[1]+1))
plt.plot(n_components_list, np.cumsum(var_rate)) # cumsum局部元素累加
plt.xticks(n_components_list) # 这是为了限制坐标轴显示为整数
plt.xlabel("number of components")
plt.ylabel("std_rate")
plt.show()
"""★ 关于n_components
关于主成分个数的确定, 在scikit-learn中调用pca = PCA(n_components=n)时,有两种定义方式:
- 1.一种是把n设置成整数,比如n=3,表示要保留三个主成分,即新坐标轴有三个维度.
- 2.一种是把n设置成小数,假设所有特征向量加起来的贡献率是1,假定要0.95的主成分贡献率,就令n=0.95
那么就会按特征值从大到小一直加到累计贡献率大于等于0.95的特征向量个数. 最终就会降到那个维.
>> 第一种是偏向于指定维度的数量,第二种则偏向于指定主成分的保留程度。
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 皮尔逊相关系数
import pandas as pd
import seaborn as sns
import numpy as np
data = pd.DataFrame(data=np.random.randint(0,1000,size=(100,5))) # 生成示例数据
corr_matrix = data.corr().abs() # 计算相关系数矩阵,abs取绝对值
# 输出相关系数矩阵
print("相关系数矩阵:")
print(corr_matrix)
# 绘制热力图
sns.heatmap(corr_matrix,cmap='Reds',annot=True)
2
3
4
5
6
7
8
9
10
11
12
13
# F检验
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.feature_selection import SelectKBest # 特征选择器
from sklearn.feature_selection import f_regression # F检验算法
"""
feature_selection.f_classif (F检验-分类场景)
feature_selection.f_regression(F检验-回归场景)
"""
data = load_diabetes()
X = data.data # 特征矩阵
y = data.target # 目标向量
k = 5 # 需要选择的特征数量
selector = SelectKBest(score_func=f_regression, k=k) # score_func选择F检验的方案
X_new = selector.fit_transform(X, y)
scores = selector.scores_ # 获取每个特征的F统计量,F统计量越高表示该特征越重要
selected_features = selector.get_support(indices=True) # 获取被选择特征的下标
# 打印被选择的特征
new_X = X[:,selected_features] # 或者直接打印 X_new
new_X
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 卡片过滤
from sklearn.feature_selection import SelectKBest #特征选择器
from sklearn.feature_selection import chi2 #卡方检验算法
from sklearn import datasets
data = datasets.load_breast_cancer()
X = data.data # 特征矩阵
y = data.target # 标签向量
# 将特征矩阵X和目标变量y传入chi2函数进行特征选择
selector = SelectKBest(chi2, k=5) # k表示选择的特征数量,可以根据需要进行调整
X_new = selector.fit_transform(X, y)
X_new # 获得特征选择后的特征数据
scores = selector.scores_ # 获取每个特征的卡方统计量,卡方统计量越高表示该特征越重要
scores
selected_features = selector.get_support(indices=True) # 输出选中的特征的索引
selected_features
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 互信息
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif
from sklearn import datasets
"""
- feature_selection.mutual_info_classif -- 互信息分类
- feature_selection.mutual_info_regression -- 互信息回归
"""
data = datasets.load_wine()
X = data.data
y = data.target
# k表示选择的特征数量, 可以根据需要进行调整
selector = SelectKBest(mutual_info_classif, k=5)
# 获得特征选择后的特征数据
X_new = selector.fit_transform(X, y)
scores = selector.scores_ # 获得每个特征的互信息量的估计
scores
selected_features = selector.get_support(indices=True) # 输出选中的特征的索引
selected_features
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# KNN分类模型
# 基本使用
"""该示例是一个以年龄、性别、工作时长、职位等特征预测年收入的案例"""
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
data = pd.read_csv('./adults.txt').drop(columns='Unnamed: 0')
data
feature = data.loc[:,data.columns != 'salary'] # 特征 "除salary列,其它列都作为特征"
target = data['salary'] # 标签
feature.info() # 看看特征的数据类型,便于接下来特征工程的工作
# - 特征工程:性别特征值化 > 性别是无序的,独热编码
ret = pd.get_dummies(feature['sex'])
feature = pd.concat((feature,ret),axis=1).drop(columns='sex')
# - 特征工程:工作岗位特征值化
# > 看你怎么思考,工作岗位与薪资档位挂钩,那就是有序的;单纯的工作岗位,就是无序的! 这里我们认为是有序的,标签编码
dic = {}
index = 1
for occ in feature['occupation'].unique():
dic[occ] = index
index += 1
feature['occupation'] = feature['occupation'].map(dic)
# - 特征工程:对特征进行无量纲化的处理!
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
# tool = MinMaxScaler() # 若用它,最后预测得分是0.801473
tool = StandardScaler() # 若用它,最后预测得分是0.792722
m_feature = tool.fit_transform(feature)
m_feature
# - 特征工程:因为该数据集特征比较少,根据个人经验判断无需做特征选择! 若需选择,可以用互信息先试一下.
# - 数据集二八分
x_train,x_test,y_train,y_test = train_test_split(m_feature,target,test_size=0.2,random_state=2020)
# - 开始进行KNN分类
model = KNeighborsClassifier(n_neighbors=5) # 注意:n_neighbors的值必须小于等于样本数量!!
model.fit(x_train,y_train) # 喂数据
res = model.score(x_test,y_test) # 预测打分,x_test输入模型中,将结果与标准答案y_test进行对比,看正确的占比
res
# PS: 查看预测的结果 model.predict(x_test)
""" KNeighborsClassifier() 的参数说明: / 模型超参数
1. n_neighbors - 算法原理中的K值,即KNN算法选择的最近邻样本的数量
2. weights
- 权重,用于指定最近邻样本的投票权重!
- 常见的选择有"uniform"(所有样本的权重相等)和"distance"(给更近的邻居更高的权重)
- why? "distance"考虑了距离更近的邻居对分类的重要性,可以在样本数量较少或数据类别分布不平衡的情况下提高模型性能
比如:训练集有100个样本,其中猫80个,狗20个.类别数量差异大. -- 可通过 y_train.value_counts() 查看!!
3. metric
- 距离度量,用于计算未知项与样本之间的距离
- ★ 一般来说,欧氏距离适用于连续性且量纲相同的数据;曼哈顿距离适用于具有离散性特征或有不同量纲的数据;
闵可夫斯基距离可以根据具体情况灵活选择参数p来平衡距离衡量的效果.(P=1曼哈顿距离、P=2欧式,当然P可设置为1.1 1.2之类的)
- ★ Q:所有特征中既有连续形特征又有离散形特征.那我用哪个度量单位呢?
A:只能试!!因为你压根不知道当前数据集在空间中的分布情况是怎样的.不同的数据集情况不一样,哪个效果好就用哪个!!
"""
"""
上述情况中,影响预测打分的因素有: 工作岗位特征有序无序的判断;无量纲化的选择;k值的选定..、随机数种子的取值等
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# 交叉验证+学习曲线
"""该示例是一个以年龄、性别、工作时长、职位等特征预测年收入的案例"""
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
data = pd.read_csv('./adults.txt').drop(columns='Unnamed: 0')
feature = data.loc[:,data.columns != 'salary']
target = data['salary']
ret = pd.get_dummies(feature['sex'])
feature = pd.concat((feature,ret),axis=1).drop(columns='sex')
dic = {}
index = 1
for occ in feature['occupation'].unique():
dic[occ] = index
index += 1
feature['occupation'] = feature['occupation'].map(dic)
tool = MinMaxScaler()
m_feature = tool.fit_transform(feature)
#######
# !!! 上面的代码跟基本使用里一样,下面开始交叉验证的代码!!
#######
from sklearn.model_selection import cross_val_score
import numpy as np
import matplotlib.pyplot as plt
ks = np.linspace(2,50,num=30).astype('int') # 存放的是n_neighbors的待选值
scores = [] # 每一个 k/n_neighbors 对应的模型评分
for k in ks:
model = KNeighborsClassifier(n_neighbors=k)
# !!看到没,无需数据集手动二八分,无需手动fit,无需手动score,交叉验证内部就做了!!
# cross_val_score()其cv=5. 证明该函数会返回5次评估结果,我们mean()取其均值.
score = cross_val_score(model,m_feature,target,cv=5).mean()
scores.append(score)
scores = np.array(scores)
index = np.argmax(scores) # 找到最高分值对应的下标
best_k = ks[index] # 根据上一步得到的下标去ks中找到对应的k值!
print('最优的k值为:',best_k)
# 绘制学习曲线
plt.plot(ks,scores)
plt.xlabel('ks')
plt.ylabel('scores')
plt.show()
# ◎ 测试新数据集的流程
# - 用上面交叉验证使用的数据集进行建模,然后将新数据集输入到这个模型中进行预测!
# model = KNeighborsClassifier(n_neighbors=best_k)
# model.fit(m_feature,target) # 用旧的数据集进行建模
# > To do 新数据集拆分出特征和标签,新数据的特征需要进行跟旧数据一样的特征工程!!
# res = model.score(新数据集经过特征选择的特征,新数据集的标签)
# res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 线性回归模型LinearRegression
# 使用最小二乘法
"""示例:波士顿房价"""
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
import warnings
warnings.filterwarnings('ignore')
data = load_boston()
feature = data.data
target = data.target
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
linner = LinearRegression() # 一元回归多元回归都使用的是LinearRegression,该示例中是多元线性回归
linner.fit(x_train,y_train) # 训练模型 这一步很关键,它会应用最小二乘法找到w向量的最优值
linner.intercept_ # 返回截距
linner.coef_ # 每一个特征维度的权重系数w
[*zip(data.feature_names,linner.coef_)] # 将权重系数和特征名称结合在一起查看
linner.score(x_test,y_test) # 评估模型
linner.predict(x_test[0].reshape(1,-1)) # 预测 predict的参数是X,表示得传矩阵 1行,-1自动计算列
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 使用梯度下降(没有调参)
"""示例:波士顿房价"""
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
boston = load_boston()
feature = boston.data
target = boston.target
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2,random_state=2020)
# ★★★★★ 无量纲化操作!!!
# 在实现梯度下降前, 基本上都会先对样本数据的特征(训练集和测试集的特征)进行归一化或者标准化的无量纲化操作
# 使得梯度下降算法更加稳定和快速
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 训练模型
model = SGDRegressor() # Todo:可以调参进行模型的优化!!
model.fit(x_train, y_train)
# 评估模型
model.score(x_test, y_test)
# 预测
model.predict(x_test[0].reshape(1,-1))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 回归模型评价指标 R-Square
# 模型评估
*MSE、MAE、R-Square
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression # 最小二乘法
from sklearn.metrics import mean_squared_error as MSE, mean_absolute_error as MAE, r2_score # MSE、MAE、R^2
df = pd.read_excel('./house.xlsx')
df.shape,df.columns
ex = df.columns != 'Y house price of unit area' # array([ True, True, True, True, True, True, False])
# - 特征
feature = df.loc[:,ex] # 取除了标签列的其它列 也可以 df.iloc[:,:-1]
# - 标签
target = df['Y house price of unit area']
# TO do:特征工程
# - 二八分
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
# - 建模
linner = LinearRegression()
linner.fit(x_train,y_train)
# - 模型评估(基于训练集对模型进行评估 MSE、MAE、R^2)
# print('模型在训练集上的表现:',linner.score(x_train,y_train))
y_true = y_train
y_pred = linner.predict(x_train)
ret_train = MSE(y_true,y_pred), MAE(y_true,y_pred), r2_score(y_true,y_pred)
print('模型在训练集上的表现效果:', ret_train)
# - 模型评估(基于测试集对模型进行评估 MSE、MAE、R^2)
# print('模型在测试集上的表现:',linner.score(x_test,y_test))
y_true = y_test
y_pred = linner.predict(x_test)
ret_test = MSE(y_true,y_pred), MAE(y_true,y_pred), r2_score(y_true,y_pred)
print('模型在测试集上的表现效果:', ret_test)
"""
看测试集标签数据的指标,通常会与MAE进行比较..
"""
import numpy as np
y_test.min(),y_test.mean(),np.median(y_test),y_test.max()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 评估的交叉验证
MSE、MAE、R^2都可以通过交叉验证来实现 以MSE为例
from sklearn.model_selection import cross_val_score
model = LinearRegression()
# - scoring默认值为None,表示正确率,用于knn分类场景中;
# scoring值为neg_mean_squared_error,表示用均方误差来评估,用于回归的场景.
# - 均方误差不可能是负数,但交叉验证认为误差就是损失,是损失就用负数来表示
mse_array = cross_val_score(model,feature,target,cv=5,scoring='neg_mean_squared_error')
mse_array_mean = mse_array.mean()
# (array([-12.46030057, -26.04862111, -33.07413798, -80.76237112, -33.31360656]), -37.131807467699204)
mse_array,mse_array_mean
2
3
4
5
6
7
8
9
10
# 多项式回归模型(解决欠拟合)
我们先对数据集二八分后直接LinearRegression, 通过评价指标观察模型在测试集和训练集上的效果都很差, 欠拟合..
于是乎, 增加2次项特征后二八分,再LinearRegression, 看模型在测试集上的效果.
(MAE)损失减小了, (R^2)拟合程度升高了.. 改进是有效的!
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error as MSE, mean_absolute_error as MAE, r2_score
from sklearn.preprocessing import PolynomialFeatures
df = pd.read_excel('./house.xlsx')
ex = df.columns != 'Y house price of unit area'
feature = df.loc[:,ex] # - 特征矩阵
target = df['Y house price of unit area'] # - 标签
# TO do:特征工程
# - 直接LinearRegression
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
linner = LinearRegression()
linner.fit(x_train,y_train)
print("直接LinearRegression 训练集:",
MSE(y_train,linner.predict(x_train)),
MAE(y_train,linner.predict(x_train)),
linner.score(x_train,y_train))
print("直接LinearRegression 测试集:",
MSE(y_test,linner.predict(x_test)),
MAE(y_test,linner.predict(x_test)),
linner.score(x_test,y_test))
# - 增加2次项特征
tool = PolynomialFeatures(degree=2,include_bias=False)
_X = tool.fit_transform(feature) # - 增加2次项特征
x_train,x_test,y_train,y_test = train_test_split(_X,target,test_size=0.2,random_state=2020)
linner = LinearRegression()
linner.fit(x_train,y_train)
print("二次项 测试集:",
MSE(y_test,linner.predict(x_test)), MAE(y_test,linner.predict(x_test)), linner.score(x_test,y_test))
# - 增加3次项特征
tool = PolynomialFeatures(degree=3,include_bias=False)
_X = tool.fit_transform(feature) # - 增加3次项特征
x_train,x_test,y_train,y_test = train_test_split(_X,target,test_size=0.2,random_state=2020)
linner = LinearRegression()
linner.fit(x_train,y_train)
print("三次项 测试集:",
MSE(y_test,linner.predict(x_test)), MAE(y_test,linner.predict(x_test)), linner.score(x_test,y_test))
"""
直接LinearRegression 训练集: 83.00347064630772 6.25510395433324 0.5750984249253477
直接LinearRegression 测试集: 55.33406050090625 5.864318119087172 0.6108181277767574
二次项 测试集: 30.83017896800291 4.179896424980049 0.783161642880907
三次项 测试集: 33.962056983913534 4.383682602356716 0.7611341585652214
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# L2 - Ridge岭回归
# 使用LinearRegression - 过拟合
import mglearn
feature,target = mglearn.datasets.load_extended_boston() # 提取样本数据
feature.shape # (506, 104)
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020) # 切分数据集
# 建模
linner = LinearRegression()
linner.fit(x_train,y_train)
print('模型在测试集上的表现:',linner.score(x_test,y_test))
print('模型在训练集上的表现:',r2_score(y_train,linner.predict(x_train)))
"""
模型在测试集上的表现: 0.6686661366503788
模型在训练集上的表现: 0.9390074922223918
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Ridge
使用岭回归, 你会发现, 岭回归和LinearRegression相比:
1> 模型在测试集上的表现提升了
2> 模型在训练集上的表现降低了.
这是由于岭回归对w的约束性, 因此不容易出现过拟合;
复杂度更小的模型(即对训练数据的依赖,就像那条线将所有点连在一起,不可取)意味着在训练集上的性能更差, 但泛化性能更好..
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
import pandas as pd
from sklearn.linear_model import Ridge
feature,target = mglearn.datasets.load_extended_boston()
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
ridge = Ridge()
ridge.fit(x_train,y_train)
print('测试集的表现:',r2_score(y_test,ridge.predict(x_test)))
print('训练集的表现:',r2_score(y_train,ridge.predict(x_train)))
"""
测试集的表现: 0.8641062336061938
训练集的表现: 0.8594543991207866
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# alpha
增大 alpha 会使得系数更加趋向于 0, 从而降低训练集性能, 但可能会提高泛化性能;
减小 alpha 可以让系数受到的限制更小.
from sklearn.linear_model import Ridge
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
feature,target = mglearn.datasets.load_extended_boston()
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
ridge = Ridge(alpha=0.1)
ridge.fit(x_train,y_train)
print('测试集的表现:',r2_score(y_test,ridge.predict(x_test)))
print('训练集的表现:',r2_score(y_train,ridge.predict(x_train)))
"""
测试集的表现: 0.8803150210251306
训练集的表现: 0.906437392554942
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 交叉验证+学习曲线求alpha
线性模型的弊端就是对数据集要求极高, 如果数据集没有线性关系, 线性回归的效果就极差, r2就会出现负值的情况.
所以只能通过相关的特征工程或者正则化等方式处理样本数据. 如果效果还差, 就只能考虑更换模型..
from sklearn.linear_model import Ridge
import mglearn
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import cross_val_score
ks = np.arange(0.1, 1.1, 0.1)
scores = []
feature,target = mglearn.datasets.load_extended_boston()
for k in ks:
model = Ridge(alpha=k)
score = cross_val_score(model,feature,target,cv=5,scoring="r2")
scores.append(score)
scores,np.mean(scores,axis=1)
"""
([array([ 0.76316425, 0.72062815, 0.84571616, 0.39002587, -1.26196327]),
array([ 0.79641879, 0.77023336, 0.87370586, 0.39466933, -0.44690815]),
array([ 0.80658939, 0.78981878, 0.87512496, 0.3910105 , -0.06628362]),
array([0.81023625, 0.79893751, 0.86933836, 0.38457065, 0.15526839]),
array([0.81128946, 0.80336549, 0.8612893 , 0.3773208 , 0.2969641 ]),
array([0.81112555, 0.80537836, 0.85263515, 0.37004929, 0.39208166]),
array([0.81033555, 0.8060368 , 0.84400143, 0.36308708, 0.45762363]),
array([0.8092072 , 0.80589257, 0.83563153, 0.35656789, 0.50334757]),
array([0.80789287, 0.80525567, 0.82761316, 0.35053465, 0.53529366]),
array([0.80647807, 0.80431046, 0.81996733, 0.34498719, 0.55740394])],
array([0.29151423, 0.47762384, 0.559252 , 0.60367023, 0.63004583,
0.646254 , 0.6562169 , 0.66212935, 0.665318 , 0.6666294 ]))
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# L1- Lasso套索回归
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.linear_model import Lasso
feature,target = mglearn.datasets.load_extended_boston()
x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)
model = Lasso()
model.fit(x_train,y_train)
print('测试集的表现:',r2_score(y_test,model.predict(x_test)))
print('训练集的表现:',r2_score(y_train,model.predict(x_train)))
print((model.coef_ != 0).sum())
"""
测试集的表现: 0.22140772570108602
训练集的表现: 0.23183091909679454
4
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
出现了欠拟合, 通过最后一行代码我们可以知道模型只用到了104个特征中的 4 个.
我们用的是默认值 alpha=1.0, 为了降低欠拟合, 我们尝试减小 alpha, 这么做的同时, 还可以增加 max_iter 的值(迭代的最大次数).
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.linear_model import Lasso
feature,target = mglearn.datasets.load_extended_boston()
train_test_split(feature,target,test_size=0.2,random_state=2020)
model = Lasso(alpha=0.001,max_iter=1000)
model.fit(x_train,y_train)
print('测试集的表现:',r2_score(y_test,model.predict(x_test)))
print('训练集的表现:',r2_score(y_train,model.predict(x_train)))
print((model.coef_ != 0).sum()) # lasso模型将样本的104个特征压缩到了64个特征
"""
测试集的表现: 0.8774848120292482
训练集的表现: 0.9193296644855472
69
"""
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
补充下哈 查看多项式回归 的系数 截距 的代码... 就是 前面的w权重系数.. 截距可看作诗 x的0次项...
误差小 所有点串起来 过分依赖训练集的数据 过拟合!!
loss(w) = 原损失函数 + 正则项
要使loss(w)最小, 等式右边的两部分 原损失函数和正则项的值也都尽可能的小.
- L1 的表达式是权重系数的绝对值之和
尽量将那些对模型影响较小的特征(不重要特征)的权重系数变为零, 而重要特征对应的权重系数则会保留较大的值!
因此,L1正则化可以通过将一些不重要的特征的权重系数压缩到0来实现特征选择
- L2 的表达式里有平方
平方使得较大的权重系数被放大,从而产生更大的惩罚效果 促使模型减小这些特征的权重
L2正则化对于接近于0的权重系数的影响较小,对它们施加了较小的惩罚
- L1与L2
所以,L1正则化主要用于特征选择,它将不重要特征的权重系数压缩到0,只保留下重要的特征.
而L2正则化可以降低所有特征的权重系数,但一般不会被压缩到零,它通过控制所有特征的权重系数来控制模型的复杂度.
> 因此,正则化进行了特征选择、控制了模型的复杂度后,也同样可以处理模型出现的多重共线性的现象,所谓一举两得.
表达式前面的λ 用了控制约束的力度! 越大约束越大! 模型的泛化能力就可能越强.相对的,越大模型在训练集上的性能就会降低.
这里要记住的是,如果有足够多的训练数据,正则化变得不那么重要,并且岭回归和线性回归将具有相同的性能。
**为了降低欠拟合,我们尝试减小 alpha????** -- 因为正则是解决过拟合的,减少alpha,减少约束!!
理解是否正确 以实际反馈为准 自己理解说出来更好 概念啥的专业啥的让人觉得你反而不懂
------
线性回归 预测的值 该值的含义比如是房价.. 逻辑回归也是根据模型预测出值 该值的含义是概率..概率是线性的.. 再根据概率进行二分类..
no!!! 应该是几率 几率经过sigon函数压缩后才是概率!!
在sigmoid函数图像上的x轴, 即自变量.. 是数据集的 因变量/标签 吧?
线性是直线,非线性曲线??? no
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
补充
连续型与离散型数据通常指的是标签, 连续型(无限,有度量单位的)-回归预测、离散型(有线,可分)-分类
★ 关于线性与非线性 > 线性即自变量与因变量之间的关系是线性的!!
- 线性与非线性取决于单位变化的自变量对因变量的影响是否是恒定的!
举个例子,y=w1x+w0 x从1变为2,2变为3,y的值是等差的!! (这是一元的例子)
多元同理,每次只看其中一个特征,y=w1x1+w2x2+w0, x1从1变成2,2变成3,y的值也是等差的!! (这是多元的例子)
多项式同理,我们可以通过 特征升维/将多次的自变量看作一个变量,增加了特征个数,多项式就变成了多元!! (这是多项式的例子)
- 而一元、多元、多项式 回归模型的函数的图像(几何图像),并不仅是一条直线
- 一元线性 > 一元一次函数 > 二维直角坐标系中的一条直线
- 二元线性 > 二元一次函数 > 在空间坐标系中是一个平面
- n元线性 > n元一次函数 > 超平面!!
- 多项式回归 > 比如一元二次函数 y=w0x^2+w1x+w0 > 在二维直角坐标系中是一条抛物线
线性与非线性从两方面来看,一是几何图像,一是权重系数的影响!
回归模型的线性指的是第二种,单位变化的自变量(其它自变量不动)导致因变量的变化幅度是恒定的,取决于权重系统的大小!!
1. 一元 -- 特征数变多了 -- 多元 -- 线性代数 > y = WT*X
> 求最小损失/权重系数最优解真实值与预测值相减之和 > 抵消正负,平方,平方导致扩大的误差 > 除以样本数 即得到均方误差!
2. 多项式 -- 特征升维/增加特征数据 -- 多元
天气多少度,回归;天气阴晴雨,分类.
knn,k个最近的类别表决,分类;k个最近点平均值,回归.
回归模型,有个坐标是预测值,另一个坐标是特征向量 -- 预测;线性模型,两个坐标都是特征,点自身代表分类 -- 分类!!
var方差 每个真实点减去均值的平方和除以样本数 -- 平均到每个标签的信息量大小
MSE均方误差 每个点真实值减去预测值的平方和除以样本数据 -- 平均到每个样本的损失
(前面大半部分拟合,后面小部分不拟合,误差均分了,mse就小了,但这样的模型是偏科的,所以需要评价指标R^2)
R^2 = 1 - MSE/var -- 最终值越大越好,也表示拟合程度!!
线性关系的特征和标签可以用 回归模型预测值, 非线性关系的特征和标签呢????
你不知道数据集分布是咋样的,一切以最后评估结果说话.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
