pandas数据清洗

前面的博客我们学习了pandas的基本操作. 该篇博客我们来浅谈下pandas的数据清洗.

数据清洗是指对原始数据进行处理和转换, 以去除无效、重复、缺失或错误的数据, 使数据符合分析和建模的要求.
它有三个清洗维度:
-1- 缺失值处理. 对于缺失的数据, 可以删除包含缺失值的行或列或者填充缺失值.
-2- 重复值处理. 识别和删除重复的数据行, 避免重复数据对分析结果产生误导.
-3- 异常值处理. 检测和处理异常值, 决定是删除、替换或保留异常值.

# 缺失值清洗

★ 敲黑板:
实现空值的清洗最好选择删除的方式, 如果删除的成本比较高(eg: 原本有50行,删除后就只有5行), 再选择填充的方式.

换个说法: 若行/列的空值占比高,我们就删除空值所在的行/列. 否则对这一行/列的空值进行填充

# 缺失值的个数和占比

■ 该示例中计算了每列的缺失值的个数和占比, 每行的计算同理.

注意两个点,这段测试代码就看得懂了: -1- df['A'] 、df[0] -2- True==1、False==0

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan

print(df)

for col in df.columns:  # col表示df的某一列的列索引
    if df[col].isnull().sum() > 0:  # 判断列中是否存在空值
        p = df[col].isnull().sum() / df[col].size  # 计算空值的占比
        p = format(p, '.2%')  # .2%表示将p转换成保留2位小数的百分数
        print(f'索引下标为{col}的列中 存在空值的占比为:{p}')
    else:
        print(f'索引下标为{col}的列中 不存在空值')

"""
    0   1     2     3   4
0  35  92  58.0   NaN   2
1  91  74  53.0  43.0  97
2  73  30   NaN  97.0  33
3  38  79  85.0   NaN  98
4  58  80   1.0  82.0  97
5  80  78   4.0   NaN  21
6  33  87  32.0  33.0  30

索引下标为0的列中 不存在空值
索引下标为1的列中 不存在空值
索引下标为2的列中 存在空值的占比为:14.29%
索引下标为3的列中 存在空值的占比为:42.86%
索引下标为4的列中 不存在空值
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 缺失值/空值的删除

缺失值/空值的删除所涉及的方法

方法	含义
isnull()	检测df中的每一个元素是否为空值, 为空则给该元素返回True, 否则返回False
notnull()	检测df中的每一个元素是否为非空值, 为非空则给该元素返回True, 否则返回False
any()	检测一行或一列布尔值中是否存在一个或多个True, 有则返回True, 否则返回False
all()	检测一行或一列布尔值中是否存全部为True, 有则返回True, 否则返回False
dropna()	将存在缺失值/空值的行或者列进行删除

# isnull() + any()

■ isnull()结合any()进行空值检测和过滤

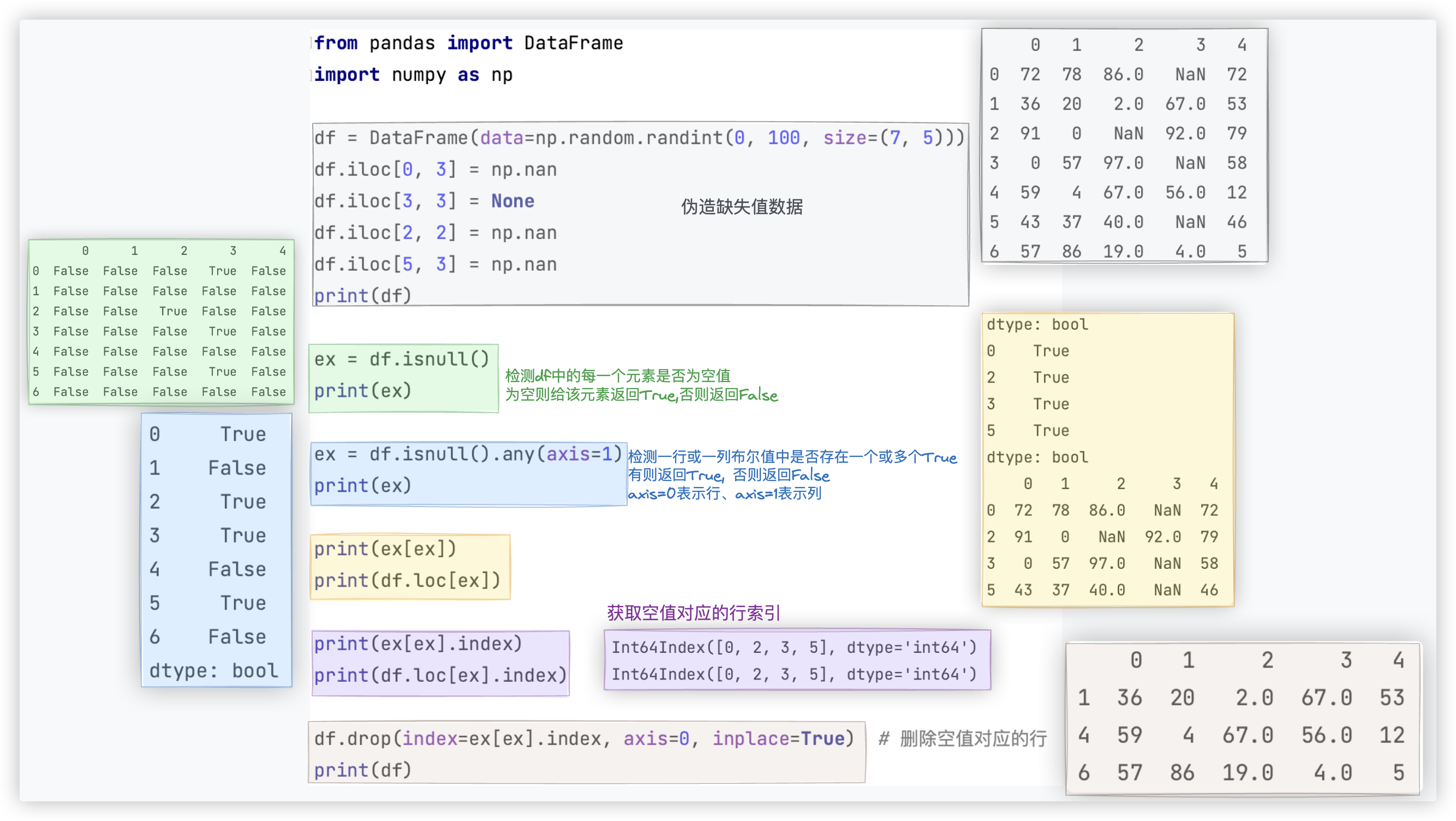
Ps: 截图中说, axios=0表示行, axis=1表示列. 这样表达不够严谨.
应该说, axios=0是指行的索引,竖直方向、axios=1是指列的索引,水平方向.

测试代码如下:

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan
print(df)

ex = df.isnull()
print(ex)

ex = df.isnull().any(axis=1)
print(ex)

print(ex[ex])
print(df.loc[ex])

print(ex[ex].index)
print(df.loc[ex].index)

df.drop(index=ex[ex].index, axis=0, inplace=True)  # 删除空值对应的行
print(df)

"""
其实感觉复杂了 直接 df[~ex] 就得到啦!! 我真聪明 (*≧ω≦)
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# notnull() + all()

■ notnull()结合all()进行空值检测和过滤

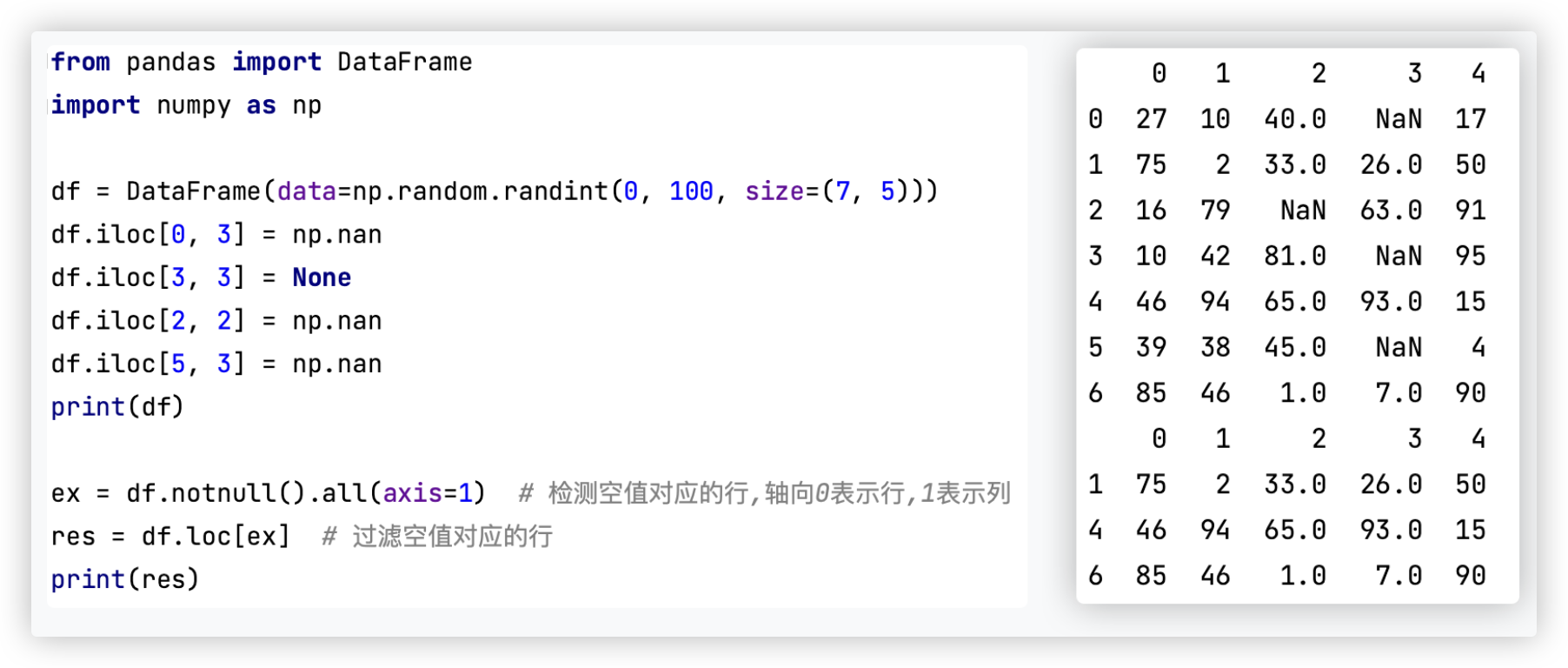
测试代码如下:

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan
print(df)

ex = df.notnull().all(axis=1)  # 检测空值对应的行,轴向0表示行,1表示列
res = df.loc[ex]  # 过滤空值对应的行  res=df[ex] 一样的
print(res)

1
2
3
4
5
6
7
8
9
10
11
12
13

# dropna()

■ dropna()进行空值检测和过滤

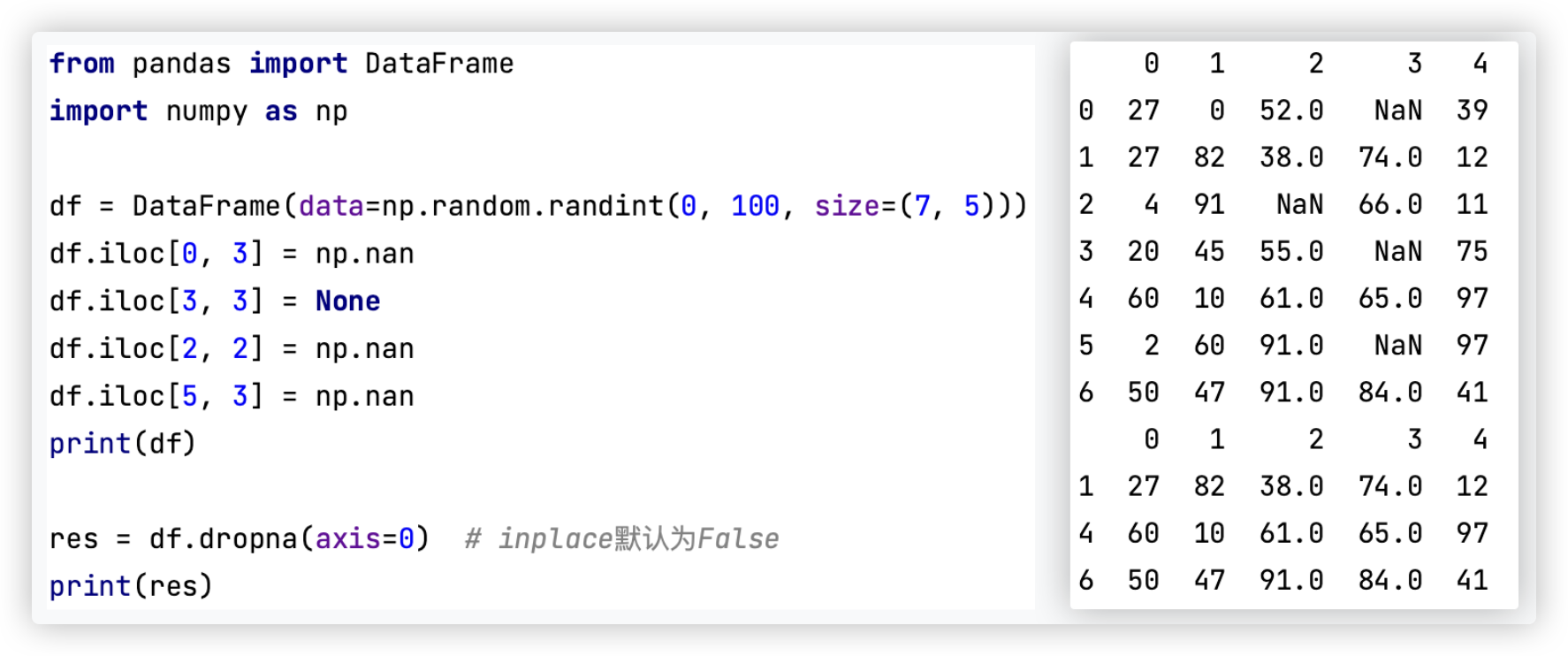
测试代码如下:

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan
print(df)

res = df.dropna(axis=0)  # inplace默认为False
print(res)

1
2
3
4
5
6
7
8
9
10
11
12

# 缺失值/空值的填充

缺失值/空值的填充一般有两种形式: -1- 用近邻值填充 ; -2- 用统计指标进行填充

# 近邻值填充

df.fillna(method='bfill',axis=0)  # axis表明在[竖直方向]上,选择空值后面的元素对空值进行填充
# (*≧ω≦) 填充方式: ffill - 前填充 和 bfill - 后填充

1
2

测试代码如下:

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan
print(df)

df.fillna(method='bfill', axis=0, inplace=True)
print(df)

"""
    0   1     2     3   4
0   9  55  31.0   NaN  66
1  83   0  84.0  27.0  48
2  55  34   NaN  16.0  74
3  90  62  82.0   NaN  97
4   4  13  69.0  17.0  53
5  22  16  90.0   NaN  97
6  61  93  63.0  26.0  65
    0   1     2     3   4
0   9  55  31.0  27.0  66
1  83   0  84.0  27.0  48
2  55  34  82.0  16.0  74
3  90  62  82.0  17.0  97
4   4  13  69.0  17.0  53
5  22  16  90.0  26.0  97
6  61  93  63.0  26.0  65
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 统计指标填充

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[0, 3] = np.nan
df.iloc[3, 3] = None
df.iloc[2, 2] = np.nan
df.iloc[5, 3] = np.nan

print(df)

for col in df.columns:
    if df[col].isnull().sum() > 0:
        mean_value = df[col].mean()  # 用每一列的均值进行填充
        df[col].fillna(value=mean_value, inplace=True)

print(df)

"""
    0   1     2     3   4
0  65  52  96.0   NaN  71
1  71  67  73.0  85.0  59
2  91  43   NaN  79.0  23
3  10  59  80.0   NaN  86
4  43  97  28.0  73.0  66
5  81  98  90.0   NaN  60
6  42  21  48.0  88.0  53
    0   1          2      3   4
0  65  52  96.000000  81.25  71
1  71  67  73.000000  85.00  59
2  91  43  69.166667  79.00  23
3  10  59  80.000000  81.25  86
4  43  97  28.000000  73.00  66
5  81  98  90.000000  81.25  60
6  42  21  48.000000  88.00  53
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

关于统计指标, 补充一点:

df[2].mean() 、df[2].median() 、df[2].std()空值、中位数、方差等都不影响均值计算
注: 众数可能会返回多个值,当元素个数出现次数都一样时.

1
2

# 重复值清洗

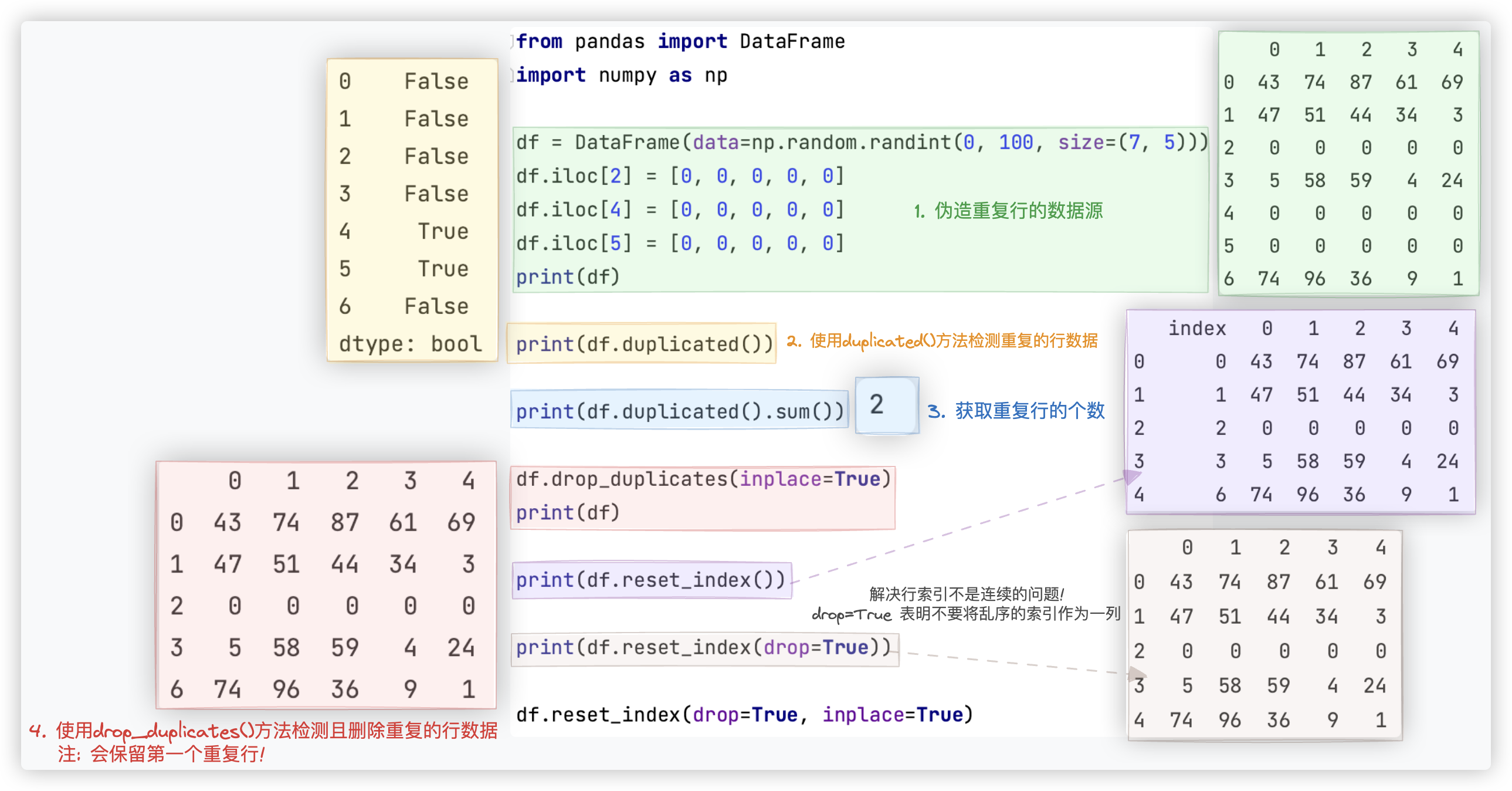
测试代码如下:

from pandas import DataFrame
import numpy as np

df = DataFrame(data=np.random.randint(0, 100, size=(7, 5)))
df.iloc[2] = [0, 0, 0, 0, 0]
df.iloc[4] = [0, 0, 0, 0, 0]
df.iloc[5] = [0, 0, 0, 0, 0]
print(df)

print(df.duplicated())
print(df.duplicated().sum())

df.drop_duplicates(inplace=True)
print(df)

print(df.reset_index())
print(df.reset_index(drop=True))
df.reset_index(drop=True, inplace=True)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 异常值清洗

异常值/疑似异常值/离群点/样本中出现的"极端值", 它需要密切注意, 否则可能导致错误的估计.

# 给定条件

给定条件的异常数据处理, 很简单, 举个例子:
自定义一个1000行3列(A,B,C)取值范围为0-1的数据源, 然后将C列中的值大于其两倍标准差的异常值进行清洗

from pandas import DataFrame
import numpy as np

data = np.random.random(size=(1000, 3))
df = DataFrame(data=data, columns=['A', 'B', 'C'])
# print(df[~(df["C"] > df["C"].std() * 2)]) 这一行代码可替代下面三行代码.  -- 结果行索引不连续reset_index解决
error_index = df["C"][df["C"] > df["C"].std() * 2].index
df.drop(labels=error_index, axis=0, inplace=True)
print(df)  # -- 结果行索引不连续reset_index解决

# ------ ------ ------

data = np.random.random(size=(1000, 3))
df = DataFrame(data=data, columns=['A', 'B', 'C'])
bool_series = df["C"] < df["C"].std() * 2
temp = df.loc[bool_series]  # df[bool_series]
temp.reset_index(drop=True, inplace=True)
print(temp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 未给定条件

★ 一组数据要么是正太的要么就是偏态的..
正太或对称分布的用标准差法; 不对称的或偏态的用MAD法; 不知道数据是正态还是偏态先用四分位数法试试..
在后面讲数据挖掘时,有方法验证数据是正态还是偏态的..
生活中基于统计得到的数据一般都是符合正态分布的,比如年龄、身高、体重..

★ 给的是DataFrame二维的, 但分析看的是一组数据,比如取一列

# 标准差法

标准差法的适用范围是符合正太分布的数据.

正态分布曲线呈钟型, 两头低, 中间高. 在正态分布中
- 约68%的数据落在平均值（μ）加减一个标准差（σ）的范围内; 
- 约95%的数据落在平均值加减两个标准差的范围内; 
- 约99.7%的数据落在平均值加减三个标准差的范围内.
因此,3倍标准差的阈值范围可以涵盖绝大部分的正态分布数据。

1
2
3
4
5

所以我们将区间[μ - 3σ,μ + 3σ] 的值视为正常值范围, 在[μ - 3σ,μ + 3σ]外的值视为离群值.
其中σ(sigma)指标准差, μ指均值.

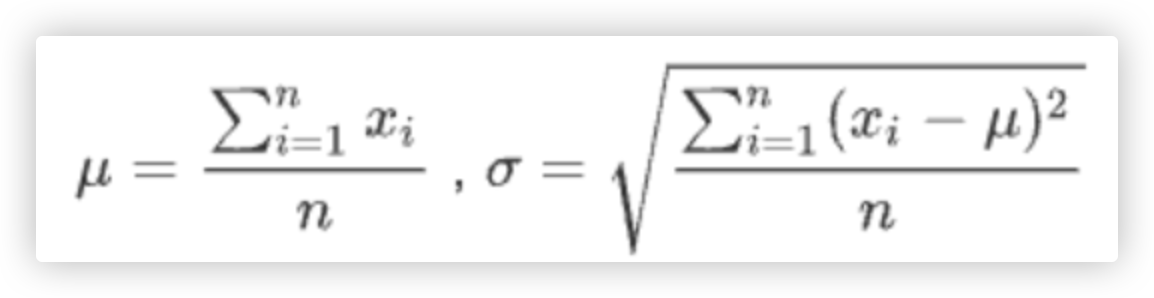
代码实现如下:

import numpy as np

# 目的: 伪造了一组含有5个异常数据的样本
iris_length = np.random.randn(9999)
# 手动添加一些异常数据
iris_length[44] = 54
iris_length[33] = 67
iris_length[22] = 56
iris_length[11] = 87
iris_length[55] = 49


def std_opt(data):
    mean_value = data.mean()  # 均值
    std_value = data.std()    # 标准差
    m_min = mean_value - 3 * std_value
    m_max = mean_value + 3 * std_value
    return m_min, m_max  # 区间范围元祖


m_min, m_max = std_opt(iris_length)

error = (iris_length < m_min) | (iris_length > m_max)
print(iris_length[error])  # [87. 56. 67. 54. 49.]
"""
for i in iris_length:
    if i < m_min or i > m_max:
        print(i)
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# MAD法

应用场景:
-1- 当数据呈对称分布或接近对称分布时MAD和标准差法效果相等或接近相等.
-2- 当数据为偏态分布, 应选择众数或中位数等位置代表值, 这时它们的代表性要比均值好.

绝对值差中位数法,是一种先需计算所有因子与中位数之间的距离总和来检测离群值的方法, 适用大样本数据

Ps: 这与标准差法中, 标准差的计算公式差不多, 只是把均值改成了中位数.

根据经验,我们将区间[X_median - 3σ,X_median + 3σ] 的值视为正常值范围
在[X_median - 3σ,X_median + 3σ]外的值视为离群值.

代码实现如下: (示例中数据是正太分布的,无伤大雅)

import numpy as np

# 目的: 伪造了一组含有5个异常数据的样本
iris_length = np.random.randn(9999)
# 手动添加一些异常数据
iris_length[44] = 54
iris_length[33] = 67
iris_length[22] = 56
iris_length[11] = 87
iris_length[55] = 49


def median_opt(data):
    median = np.median(data)  # 中位数
    count = data.size  # 这组数据个数
    # 求中位数差 <numpy的运算是会向量化的>
    temp = ((data - median) ** 2).sum() / count
    a = np.sqrt(temp)
    # 范围
    m_min = median - 3 * a
    m_max = median + 3 * a
    return m_min, m_max


m_min, m_max = median_opt(iris_length)

error = (iris_length < m_min) | (iris_length > m_max)
print(iris_length[error])  # [87. 56. 67. 54. 49.]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 四分位数法

又叫做箱型图法, 由最小值、下四分位值(25%)、中位数(50%)、上四分位数值(75%)、最大值这5个关键的百分数统计值组成的.

应用场景: 适用于数据分布非正态、存在偏斜或包含极端值的情况.
尤其适用于对数值型数据的异常值检测和过滤.但在对称且近似正态分布的数据上也可以使用.

1    2       3       4    5
    Q1     中位数     Q3
  
Q1: 25%、下四分位数
Q3: 75%、上四分位数
IQR: Q3-Q1

△ Q1-3IQR □ Q1-1.5IQR  Q1  Q3  Q3+1.5IQR □  Q3+3IQR △
温和异常值处于□的位置;极端异常值处于△的位置

1
2
3
4
5
6
7
8
9

代码实现如下:

import numpy as np


def boxplot(data):
    # 下四分位数值、中位数，上四分位数值
    Q1, median, Q3 = np.percentile(data, (25, 50, 75))
    # 四分位距
    IQR = Q3 - Q1
    # 内限
    inner = [Q1 - 1.5 * IQR, Q3 + 1.5 * IQR]
    # 外限
    outer = [Q1 - 3.0 * IQR, Q3 + 3.0 * IQR]
    print('>>>内限：', inner)  # >>>内限: [-0.5025000000000002, 1.4775000000000003]
    print('>>>外限：', outer)  # >>>外限: [-1.2450000000000003, 2.2200000000000006]

    # "过滤掉" 极端异常值
    goodData = []
    for value in data:
        if (value < outer[1]) and (value > outer[0]):
            goodData.append(value)

    return goodData


data = [0.2, 0.3, 0.15, 0.32, 1.5, 0.17, 0.28, 4.3, 0.8, 0.43, 0.67]  # 4.3是异常值
res = boxplot(data)
print(res)  [0.2, 0.3, 0.15, 0.32, 1.5, 0.17, 0.28, 0.8, 0.43, 0.67]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

← pandas基本操作 pandas数据集成→